11.6: Правило потоку

Last updated
Save as PDF

Page ID: 33048

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Найпростішу форму правила пов'язаного потоку для жорсткого ідеально пластичного матеріалу надає

\[\dot{\epsilon}_{ij} = \dot{\lambda} \frac{\partial F(\sigma_{ij})}{\partial \sigma_{ij}} \]

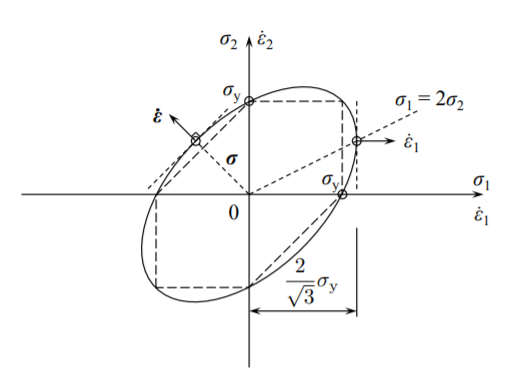
де функція\(F(\sigma_{ij})\) визначається рівнянням (11.3.8), і\(\dot{\lambda}\) є скалярним коефіцієнтом множення. Рівняння (11.3.11) однозначно визначає напрямок вектора швидкості деформації, який завжди спрямований нормально до поверхні текучості в заданій точці напруги. У випадку плоского напруження двома складовими вектора швидкості деформації є

\[\dot{\epsilon}_1 = \dot{\lambda} (2\sigma_1 − \sigma_2) \]

\[\dot{\epsilon}_2 = \dot{\lambda} (2\sigma_2 − \sigma_1) \]

Величини складових\(\dot{\epsilon}_1\) і не\(\dot{\epsilon}_2\) визначені, але співвідношення, яке визначає напрямок\(\dot{\epsilon}/\epsilon_2\), однозначно визначається.

Зокрема, під поперечними рівнинними\(\dot{\epsilon}_2 = 0\) деформаціями, так\(\sigma_1 = 2\sigma_2\) і\(\sigma_1 = \frac{2}{\sqrt{3}} \sigma_y\).

11.6.1.png — Малюнок\(\PageIndex{1}\): Вектор швидкості деформації завжди є нормальним до поверхні плинності.