11.4: Умова врожайності

З попередньої секції одновісна умова плинності при розтягуванні/стисненні в напрямку x становить

\[\sigma_{11} = \pm \sigma_y \]

У загальному 3-D всі шість компонентів тензора напружень сприяють врожайності матеріалу. Умова врожайності фон Мізеса набуває вигляду

\[\frac{1}{2} [(\sigma_{11} − \sigma_{22})^2 + (\sigma_{22} − \sigma_{33})^2 + (\sigma_{33} − \sigma_{11})^2 ] + 3(\sigma^2_{12} + \sigma^2_{23} + \sigma^2_{31})] = \sigma^2_y \]

або в коротких позначеннях

\[F(\sigma_{ij}) = \sigma_y \nonumber \]

Поетапне виведення вищевказаного рівняння наведено в наступному розділі. Тут розглядається кілька особливих випадків.

Принципова система координат

Всі недіагональні складові тензора напружень зникають,\(\sigma_{12} = \sigma_{23} = \sigma_{31} = 0\). Потім рівняння (11.3.8) зменшується до

\[ (\sigma_1 − \sigma_2)^2 + (\sigma_2 − \sigma_3)^2 + (\sigma_3 − \sigma_1)^2 = 2\sigma^2_y \]

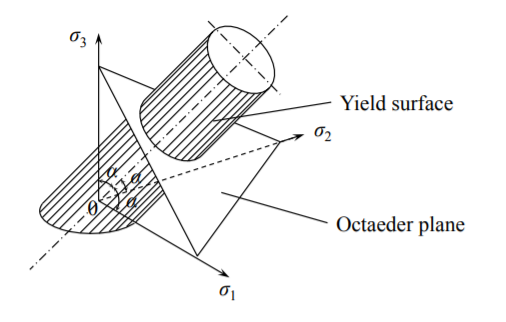
де\(\sigma_{1}\),\(\sigma_{2}\)\(\sigma_{3}\) є основними напруженнями. Графічне зображення рівняння (?? ) - відкритий циліндр, нормаль до восьмигранної площини, рис. (\(\PageIndex{1}\)).

Рівняння прямої, нормальної до восьмигранної площині і проходить через початок, дорівнює

\[\sigma_1 + \sigma_2 + \sigma_3 = 3p \]

де\(p\) - гідростатичний тиск. Оскільки гідростатичний тиск не робить ніякого впливу на врожайність, поверхня плинності являє собою відкритий циліндр.

Плоский стрес

Підставляючи\(\sigma_{13} = \sigma_{23} = \sigma_{33} = 0\) рівняння (11.3.8), умова плинності плоского напруження стає

\[\sigma^2_{11} − \sigma_{11} \sigma_{22} + \sigma^2_{22} + 3\sigma^2_{12} = \sigma^2_y \]

Рисунок\(\PageIndex{1}\): Представлення умови плинності фон Мізеса у просторі головних напружень.

Зокрема, в чистому зсуві\(\sigma_{11} = \sigma_{22} = 0\) і\(\sigma_{12} = \sigma_y/\sqrt{3}\). У літературі\(\sigma_y/\sqrt{3} = k\) називається напруга плинності при зсуві, що відповідає умові плинності фон Мізеса. У головній системі координат\(\sigma_{12} = 0\) і умова врожайності набуває простий вигляд.

\[\sigma^2_1 − \sigma_1\sigma_2 + \sigma^2_2 = \sigma^2_y \]

Малюнок\(\PageIndex{2}\): Еліпс фон Мізеса в головній системі координат.

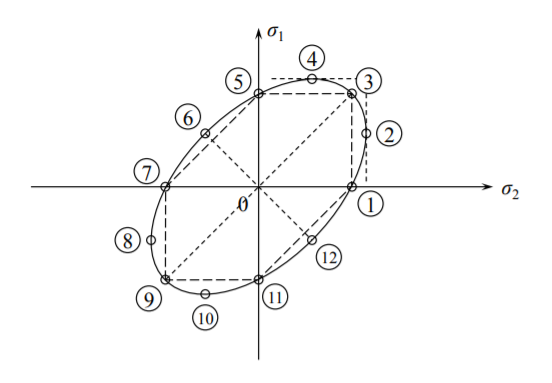
Графічне зображення рівняння (?? ) - еліпс, показаний на малюнку (\(\PageIndex{2}\)). Кілька важливих напружених станів можна виділити на малюнку (\(\PageIndex{2}\)).

• Точки 1 і 2: Одновісний натяг,\(\sigma_{1} = \sigma_{2} = \sigma_{y}\)
• Точки 7 і 11: Одновісне стиснення,\(\sigma_{1} = \sigma_{2} = -\sigma_{y}\)
• Точка 3: Рівно-двовісний натяг,\(\sigma_{1} = \sigma_{2}\)
• Точка 9: рівно-двовісне стиснення,\(-\sigma_{1} = -\sigma_{2} \)
• Точки 2, 4, 8 і 10: Звичайна деформація,\(\sigma_{1} = \frac{2}{\sqrt{3}}\sigma_{y}\)
• Точки 6 і 12: Чистий зсув,\(\sigma_{1} = -\sigma_{2}\)

Поняття площини деформації буде пояснено в розділі, присвяченому правилу потоку.

Еквівалентне напруження і еквівалентна швидкість деформації

При скінченно-елементному аналізі використовується поняття еквівалентного напруження\(\bar{\sigma}\) або напруження фон Мізеса. Визначається за принциповими напруженнями

\[\bar{\sigma} = \frac{1}{2} [(\sigma_{11} − \sigma_{22})^2 + (\sigma_{22} − \sigma_{33})^2 + (\sigma_{33} − \sigma_{11})^2 ] \]

Еквівалентним напруженням\(\bar{\sigma} (\sigma_{ij})\) є квадратний корінь лівої частини Рівняння (11.3.8). Визначивши еквівалентне напруження, енергія сполучена еквівалентна швидкість деформації може бути оцінена з

\[\bar{\sigma} \bar{\dot{\epsilon}} = \sigma_{ij} \dot{\epsilon_{ij}} \]

і дається

\[ \bar{\dot{\epsilon}} = \left\{ \frac{2}{9} [(\dot{\epsilon}_{11} − \dot{\epsilon}_{22})^2 + (\dot{\epsilon}_{22} − \dot{\epsilon}_{33})^2 + (\dot{\epsilon}_{33} − \dot{\epsilon}_{11})^2 ] \right\}^{1/2} \]

Еквівалентна деформація отримується з інтеграції в часі еквівалентної швидкості деформації.

\[\bar{\epsilon} = \int \bar{\dot{\epsilon}} dt \]