1.5: Гіпотеза Ейлера-Бернуллі

У цьому розділі часто робиться посилання на вісь балки. Значення осі балки інтуїтивно зрозуміле для призматичної балки з прямокутним перетином. Вона є середньою віссю. Інші терміни, такі як: нейтральна вісь, вісь згинання та центроїдальна вісь також часто використовуються. Всі вони виражають ту ж властивість, що ніякі осьові напруги не$\sigma_{xx}$ повинні розвиватися на осі при чистому вигині.

Гіпотеза 1: План залишається площиною

Це проілюстровано на малюнку ($\PageIndex{1}$), що показує довільне перетин балки до і після деформації.

Рисунок$\PageIndex{1}$: Плоскі (b) і (c) і викривлені (d) поперечні перерізи після деформацій.

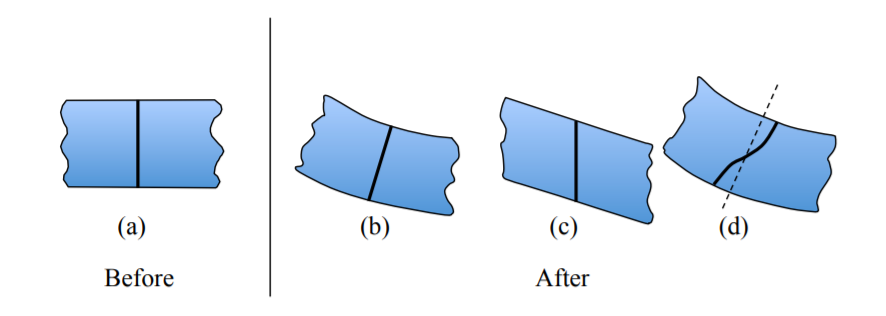
Уявіть собі прямий розріз, зроблений крізь недеформовану балку. Гіпотеза площини залишків площини означає, що всі матеріальні точки на вихідному розрізі вирівнюються також на площині в деформованому балці. Випадки (b) і (c) підкоряються гіпотезі, але викривлений розділ (d) порушує її.

Гіпотеза 2: Нормальний залишається нормальним

Якщо початковий розріз був зроблений під прямим кутом деформованої осі балки, як на малюнку$\PageIndex{2}$ (а)), він повинен залишатися нормальним до деформованої осі, див. Рис.$\PageIndex{2}$ (b)).

Малюнок$\PageIndex{2}$: Тестування гіпотези нормал-залишається нормальною.

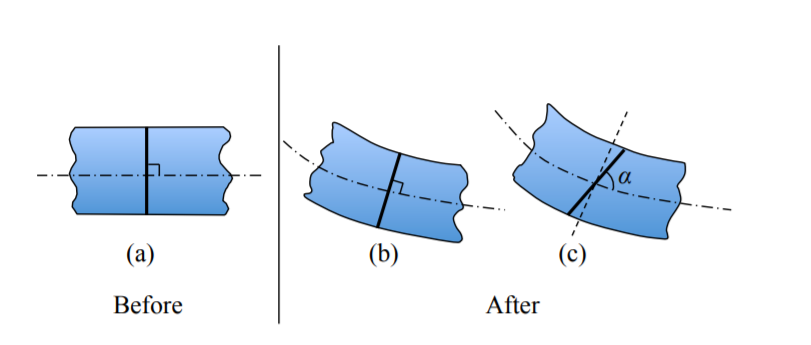
У ескізі на малюнку$\PageIndex{2}$ (в)) гіпотеза порушується при куті$\alpha \neq 90^{\circ}$.

Гіпотеза Ейлера-Бернуллі породжує витончену теорію нескінченно малих деформацій в балках з довільними перерізами та навантаженням у двох позаплощинних напрямках. Зацікавлений читач посилається на кілька монографій з детальною обробкою предмета, двоосьового навантаження балок. Справжній набір заміток на балках розроблений за припущенням площинної деформації. Це означає, що рух осі променя обмежується лише однією площиною.

Математично гіпотеза 1 задовольняється, коли u-компонент вектора зміщення є лінійною функцією$z$.

$$u(z) = u^{\circ} - \theta z \text{ at any x} \label{2.35}$$

Постійний перший член,$u^{\circ}$ - це зміщення осі балки (за рахунок осьової сили). Другий термін обумовлений одним вигином, рис. ($\PageIndex{3}$).

Малюнок$\PageIndex{3}$: Лінійне поле зміщення через товщину балок.

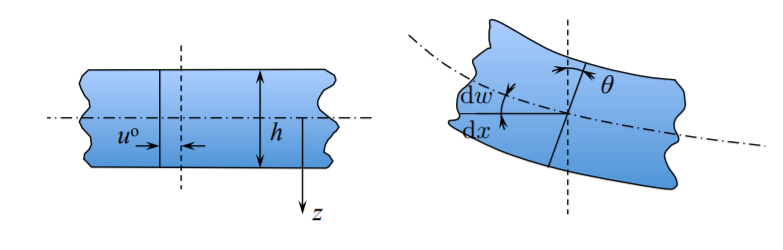
Друга гіпотеза Ейлера-Бернуллі задовольняється, якщо обертання деформованого перерізу$\theta$ дорівнює локальному ухилу зігнутої середньої осі.$\frac{ d w}{ d x}$

$$\theta = \frac{ d w}{ d x} \label{2.36}$$

Усунення кута повороту θ між рівняннями\ ref {2.35} та\ ref {2.36} дає

$$u(x, z) = u^{\circ} - \frac{ d w}{ d x}z \label{2.37}$$

З рисунка ($\PageIndex{3}$) видно, що зміщення в нижній (розтягнутій) стороні балки є від'ємним, що пояснює знак мінус у другому семестрі Рівняння\ ref {2.36} і\ ref {2.37}.

Гіпотеза 3

Форма поперечного перерізу і розмір бруса залишаються незмінними. Це означає, що вертикальна складова вектора зміщення не залежить від$z$ -координати. Всі точки поперечного перерізу переміщаються на однакову величину.

$$w = w(x) \label{2.38}$$

У разі площинної деформації, яка охоплює більшість практичних випадків відгуку променя,$y$ -складова вектора зміщення зникає

$$v = 0$$

Тепер ми в змозі обчислити всі складові тензора деформації з Рівняння (1.2.10)

$$\epsilon_{xx} = \frac{ d u_{x}}{ d x} = \frac{ d u}{ d x}$$

$$\epsilon_{zz} = \frac{ d u_{y}}{ d y} = \frac{ d v}{ d y} = 0 \text{ on account of } \ref{2.42}$$

$$\epsilon_{zz} = \frac{ d u_{zz}}{ d z} = \frac{ d w(x)}{ d z} = 0 \text{ from } \ref{2.38}$$

$$\epsilon_{xy} = \frac{1}{2} \left(\frac{ d u_{x}}{ d y} + \frac{ d u_y}{ d x} \right) = 0 \text{ from } \ref{2.37} \text{ and } \ref{2.42}$$

$$\epsilon_{yz} = \frac{1}{2} \left(\frac{ d u_{y}}{ d z} + \frac{ d u_z}{ d y} \right) = \frac{1}{2} \left(\frac{ d v}{ d z} + \frac{ d w}{ d y} \right) = 0$$

$$\begin{align} \epsilon_{zx} & = \frac{1}{2} \left(\frac{ d u_{z}}{ d x} + \frac{ d u_x}{ d z} \right) = \frac{1}{2} \left(\frac{ d w}{ d x} + \frac{ d u}{ d z} \right) \\ & = \frac{1}{2} \left(\frac{ d w}{ d x} - \frac{ d w}{ d x} \right) = 0 \nonumber \end{align}$$

Видно, що всі компоненти тензора деформації зникають, крім тієї, що знаходиться у напрямку осі пучка.

Зауважте, що$\epsilon_{xx}$ це єдиний компонент тензора деформації в теорії елементарного пучка. Тому індекс «$xx$» може бути скинутий і, якщо не вказано інше$\epsilon_{xx} = \epsilon$. Введення рівняння\ ref {2.37} в рівняння\ ref {2.38} отримує

$$\epsilon (x, z) = \frac{ d u^{\circ}(x)}{ d x} - \frac{ d ^2w(x)}{ d x^2}z$$

Перший член являє собою деформацію, що виникає при рівномірному розширенні всього поперечного перерізу.

$$\epsilon^{\circ}(x) = \frac{ d u^{\circ}(x)}{ d x} \label{2.42}$$

Другий термін додає внесок згинання. Введення визначення кривизни осі балки

$$\kappa \buildrel \rm {def} \over{=} −\frac{ d ^2w(x)}{ d x^2},$$

вираз для штаму можна поставити в кінцевому вигляді:

$$\epsilon(x, z) = \epsilon^{\circ}(x) + z\kappa$$

Математично кривизна визначається як градієнт нахилу кривої. Знак мінуса в Рівнянні (1.3.4) випливає з суворого опису кривизни прямої в передбачуваній системі координат. Фізично він передбачає, що напруги на розтягує стороні балки позитивні. Зовсім інша інтерпретація гіпотези Ейлера-Бернуллі пропонується шляхом розгляду двотермінового розширення точного профілю деформації в ряді Тейлора навколо точки.

$$\epsilon(x, z) = \epsilon(x, z) = |_{z=0} + \left. \frac{ d {\epsilon}}{ d z}\right|_{z=0} z + \left. \frac{1}{2}\frac{ d ^2 \epsilon} { d z^2}\right|_{z=0} z^2 + \ldots$$

Взяття лише перших двох членів є хорошим інженерним наближенням, але призводить до деяких внутрішніх невідповідностей теорії елементарного пучка. Ці невідповідності будуть пояснені в двох наступних розділах.