1.4: Кінематика теорії елементарного пучка

Last updated
Save as PDF

Page ID: 33096

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Слово «кінематика» походить від грецького слова «кінема», що означає руху, рух. Будь-який рух тіла передбачає\(u_i\) зсуви, їх\(du_i\) прирости і швидкості\(\dot{u}_i\). Якщо виключити переклади і обертання жорсткого тіла, розвиваються деформації. Ми часто говоримо «Кінематичне припущення» або «Кінематичні граничні умови» або «Кінематичні величини» тощо Все це означає, що висловлювання робляться про зміщення та деформації та/або їх швидкості. На відміну від цього, слово «статичний» зарезервовано для опису напружень та/або сил, навіть якщо тіло може рухатися. Справа в тому, що для статично визначених конструкцій можна було визначити напруження і сили, не викликаючи руху. Такі вирази, як «статична формулювання», «статичні граничні умови», «статичні величини» завжди відносяться до напружень і сил.

Elementary - це ще одне слово в назві цього розділу, яке вимагає пояснення. Балка - це струнка конструкція, яка може бути стиснута, витягнута або зігнута. Балка повинна піддаватися поперечному навантаженню (перпендикулярно її осі). Інакше це стає чимось іншим, як пояснено на малюнку (\(\PageIndex{1}\)).

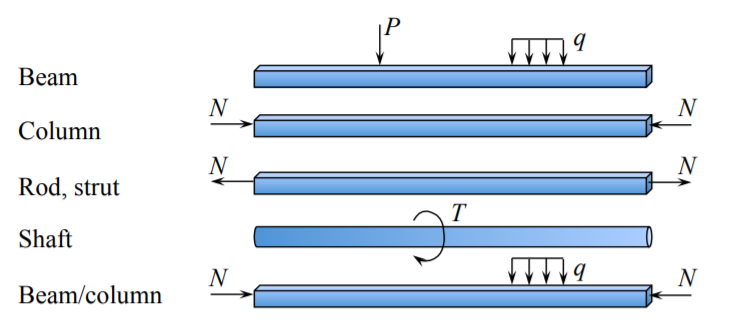
1.4.1.png — Малюнок\(\PageIndex{1}\): За типом навантаження розрізняють п'ять різних типів конструкцій.

Всі перераховані вище конструкції можуть володіти подібною стрункістю. Наскільки стрункою має бути конструкція, щоб стати пучком. Стрункість визначається як відношення довжини до товщини\(\frac{l}{h}\). Якщо\(\frac{l}{h} > 20\), балка підпорядковується спрощеним кінематичним припущенням і називається вона «балкою Ейлера». Набагато коротші балки з\(\frac{l}{h} < 10\) розвиваються значними напруженнями зсуву на додаток до напружень вигину і повинні бути оброблені іншим набором припущень. Такі балки іменуються балками Тимошенко. Проміжним діапазоном\(10 < \frac{l}{h} < 20\) є сіра область, де спрощені припущення теорії елементарного променя поступово втрачають дійсність.

У цьому розділі розглядаються балки суцільного перетину, на відміну від тонкостінних секцій. У цих конспектах лекцій послідовно використовується прямокутна\((x, y, z)\) праворучна система координат. Вісь Х спрямована по довжині балки з початком в зручне місце розташування, як правило, кінець центру балки. Вісь Y знаходиться в напрямку ширини своїм початком на площині симетрії поперечного перерізу, рис. (\(\PageIndex{2}\)). Нарешті, вісь z спрямована вниз і вимірюється від центроїдальної осі поперечного перерізу (див. Декламація 2 для визначення центроїдальної осі).

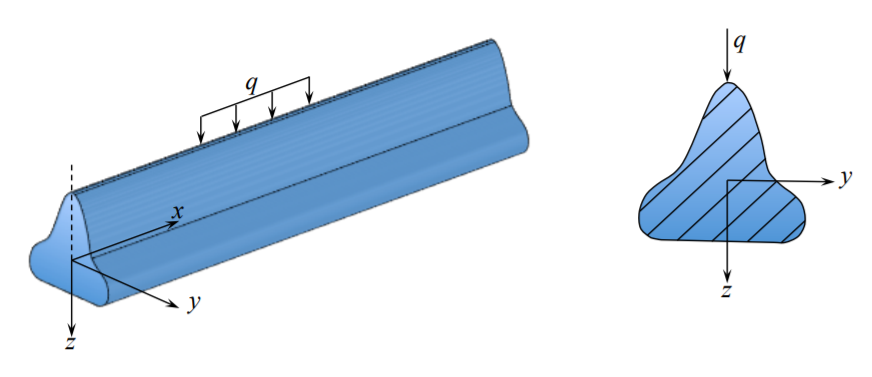
1.4.2.png — Малюнок\(\PageIndex{2}\): Призматичний стрункий пучок з симетричним перетином.

У будівельній механіці складові вектора зміщення в\(x\)\(y\), і\(z\) напрямки позначаються відповідно\((u, v, w)\). Розвиток теорії елементарного пучка ґрунтується на трьох кінематичних припущеннях. Додаткові припущення щодо стресового стану будуть введені пізніше.