11.4: Приклад масової весни
- Page ID
- 29455
Приклади в цьому розділі та наступному розділі проілюструють, як ми можемо використовувати рівняння Ейлера-Лагранжа для пошуку рівняння руху, що описує процес перетворення енергії. Розглянемо систему, що складається з маси та пружини, де енергія передається між потенційною енергією пружини, що зберігається в стиснутій пружині, та кінетичною енергією маси. Маса вказана\(m\) в кг. Він кріпиться до пружини з постійною пружиною\(K\) в\(\frac{J}{m^2}\). Положення маси задається тим,\(x(t)\) де\(x\) знаходиться залежна змінна в метрах і\(t\) є незалежною змінною часу в секундах. Припустимо, що ця маса і пружина або закріплені на рівній площині, або якимось іншим способом не впливають сили тяжіння. Ця масова пружинна система проілюстрована на лівій стороні рис. \(\PageIndex{1}\). Коли пружина стискається, система отримує потенційну енергію пружини. Коли пружина звільняється, енергія перетворюється з потенційної енергії пружини в кінетичну енергію. Припустимо, ніяких інших процесів перетворення енергії, таких як нагрівання через тертя, не відбувається.
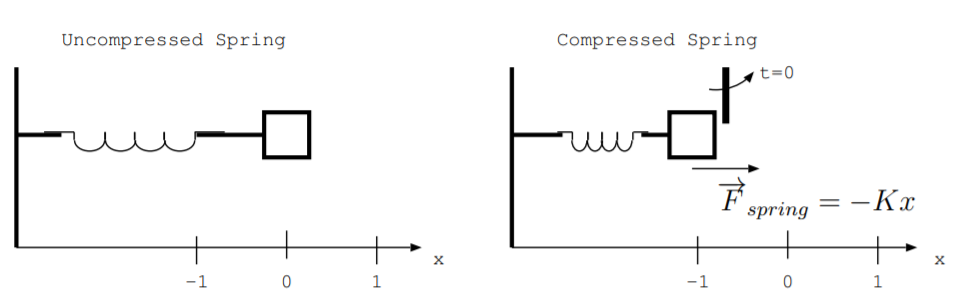
Права сторона рис. \(\PageIndex{1}\)показує стиснуту пружину, утримувану на місці обмежувачем. \(t < 0\)Бо система не має кінетичної енергії, оскільки маса не рухається, а система має потенційну енергію в стиснутій пружині. В цей час маса знаходиться в положенні\(x\) де\(x < 0\). Пружина чинить силу на масу,
\[\overrightarrow{F}_{spring}=-K x \hat{a}_{x} \nonumber \]
який знаходиться в\(\hat{a}_{x}\) напрямку.
При\(t = 0\), стриманість знімається, а потенційна енергія пружини перетворюється в кінетичну енергію. Перша форма - це пружинна потенційна енергія.
\[E_{potential\,energy} = \frac{1}{2}Kx^2 \nonumber \]
Друга форма - кінетична енергія маси.
\[E_{kinetic} = \frac{1}{2} m \left( \frac{dx}{dt} \right)^2 \nonumber \]
У будь-який момент часу, коли маса знаходиться на місці\(x(t)\), загальна енергія представлена гамільтоном.
\[H = E_{total} = E_{potential\,energy} + E_{kinetic} \nonumber \]
\[H=\frac{1}{2} K x^{2}+\frac{1}{2} m\left(\frac{d x}{d t}\right)^{2} \label{11.4.5} \]
Лагранж являє собою різницю між формами енергії.
\[\mathcal{L}=E_{potential\,energy} -E_{kinetic} \nonumber \]
\[\mathcal{L}\left(t, x, \frac{d x}{d t}\right)=\frac{1}{2} K x^{2}-\frac{1}{2} m\left(\frac{d x}{d t}\right)^{2} \nonumber \]
І гамільтоніан, і лагранж мають одиниці джоулів. Узагальнений потенціал
\[\frac{\partial \mathcal{L}}{\partial x} = Kx \nonumber \]
в одиницях ньютонів. Зауважте, що\(Kx = − \overrightarrow{F}_{spring}\). Узагальнений імпульс
\[\mathbb{M}=\frac{\partial \mathcal{L}}{\partial\left(\frac{d x}{d t}\right)}=-m \frac{d x}{d t} \nonumber \]
в одиницях\(\frac{kg \cdot m}{s}\) якого є одиниці імпульсу.
При\(t = 0\), стриманість знімається. Маса йде по шляху\(x(t)\). Якщо ми знаємо Лагранжа, ми можемо знайти шлях методом проб і помилок. Щоб знайти шлях таким чином, вгадайте шлях, за яким слідує маса\(x(t)\), і обчисліть дію.
\[\mathbb{S}=\left|\int_{t_{1}}^{t_{2}} \frac{1}{2} m\left(\frac{d x}{d t}\right)^{2}-\frac{1}{2} K x^{2}\right| d t \label{11.4.10} \]
Неодноразово вгадайте інший шлях, і прорахуйте дію. Шляхом з найменшою дією всіх можливих шляхів є шлях, яким слідує маса. Цей шлях має найменшу різницю між потенційною енергією та кінетичною енергією, інтегрованою з часом.
Ми можемо придумати багато можливих, але не фізичних шляхів,\(x(t)\) якими може слідувати маса. Малюнок\(\PageIndex{2}\) ілюструє два нефізичні шляхи, а також фізичний шлях, отриманий нижче. Шляхи розглядаються через часовий проміжок\(0 < t < 1\). Всі три шляхи припускають, що спочатку\(t = 0\), в, пружина стискається так, щоб маса перебувала в місці розташування\(x(0) = -1\). Також вони припускають, що в кінці інтервалу, в\(t = 1\), пружина розширилася так, щоб маса опинилася на місці\(x(1) = 1\). Можливі шляхи, проілюстровані на малюнку:
\[x_{1}(t)=2 t-1 \quad(\text { not physical })\nonumber \]
\[x_{2}(t)=2 t^{2}-1 \quad(\text { not physical })\nonumber \]
і
\[x_{3}(t)=-\cos (\pi t) \quad(\text { physical })\nonumber \]
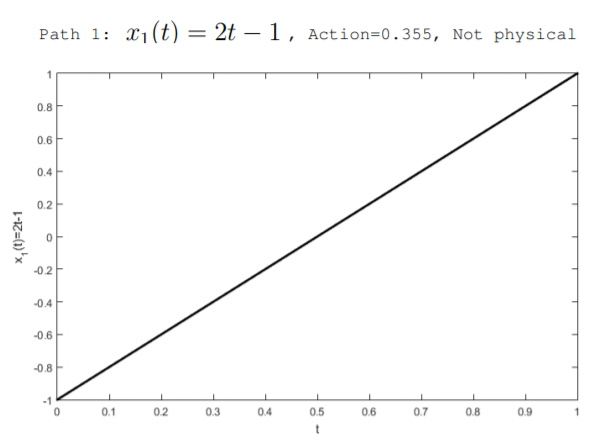
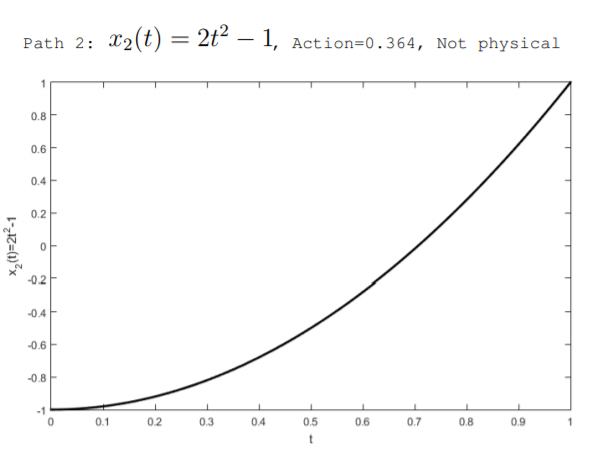
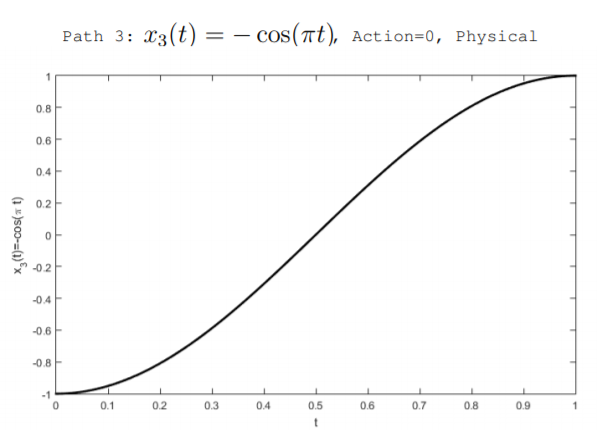
\(x_1(t)\)Шляхом описується випадок, коли маса рухається з постійною швидкістю. Шляхом\(x_2(t)\) описується випадок, коли маса прискорюється, коли обмеження знімається, а шлях\(x_3(t)\) описує випадок, коли маса спочатку прискорюється, а потім сповільнюється. Дія кожного шляху можна обчислити за допомогою Equation\ ref {11.4.10}. Для прикладу\(K = \pi^2 \frac{J}{m^2}\) використовуються значення\(m = 1 kg\) і. \(x_1(t)\)Шляхом є\(\mathbb{S} = 0.355\), шлях\(x_2(t)\) має\(\mathbb{S} = 0.364\), а фізичний шлях\(x_3(t)\) має нульову дію\(\mathbb{S} = 0\). Ми можемо вивести шлях, який мінімізує дію і який знаходиться в природі за допомогою рівняння Ейлера-Лагранжа.
\[\frac{\partial \mathcal{L}}{\partial x}-\frac{d}{d t} \frac{\partial \mathcal{L}}{\partial\left(\frac{d x}{d t}\right)}=0 \nonumber \]
Перший член - це узагальнений потенціал. Другий член - похідна за часом узагальненого імпульсу. Рівняння руху знаходять шляхом складання цих частин разом.
\[Kx+m\frac{d^2x}{dt^2} = 0 \label{11.4.12} \]
Перший член рівняння руху -\(- \left| \overrightarrow{F}_{spring} \right|\). Другий член являє собою прискорення маси. Ми щойно знайшли рівняння руху, і це твердження другого закону Ньютона, сила - це прискорення маси разів. Це також заява про збереження сили на масі.
Рівняння\ ref {11.4.12} - лінійне диференціальне рівняння другого порядку з постійними коефіцієнтами. Це відоме хвильове рівняння, і його рішення добре відоме
\[x(t)=c_{0} \cos \left(\sqrt{\frac{K}{m}} t\right)+c_{1} \sin \left(\sqrt{\frac{K}{m}} t\right) \nonumber \]
де\(c_0\) і\(c_1\) є константами, визначеними початковими умовами. Якщо ми надійно прикріпимо масу до пружини, на відміну від того, щоб дати масі вигнатися, вона буде коливатися, як описано шляхом\(x(t)\). Енергія зберігається в цій системі. Щоб перевірити збереження енергії, ми можемо показати, що загальна енергія не змінюється з часом. Загальна енергія задана гамільтоном рівняння\ ref {11.4.5}. У цьому прикладі і гамільтоніан, і лагранж явно не залежать від часу,\(\frac{\partial H}{\partial t} =0\) і\(\frac{\partial \mathcal{L}}{\partial t} = 0\). Натомість вони залежать лише від змін у часі. З цієї причини ми говоримо, що і загальна енергія, і Лагранж мають час трансляції симетрії, або ми говоримо, що вони є часом інваріантними. Весна і маса поводяться однаково сьогодні, тиждень з сьогоднішнього дня, а рік з сьогоднішнього дня.
Ми також можемо перевірити збереження енергії алгебраїчно, показавши це\(\frac{dH}{dt} = 0\).
\[\frac{d H}{d t}=\frac{\partial H}{\partial t}+\frac{\partial H}{\partial x} \frac{d x}{d t}+\frac{\partial H}{\partial\left(\frac{d x}{d t}\right)} \frac{d^{2} x}{d t^{2}} \nonumber \]
\[\frac{d H}{d t}=0+K x \frac{d x}{d t}+m \frac{d x}{d t} \frac{d^{2} x}{d t^{2}} \nonumber \]
\[\frac{d H}{d t}=\frac{d x}{d t}\left(K x+m \frac{d^{2} x}{d t^{2}}\right)=0 \nonumber \]
Зверніть увагу, що кількість в дужках у рядку вище повинна дорівнювати нулю від рівняння руху. Рівняння Ейлера-Лагранжа можна розділити на пару диференціальних рівнянь першого порядку, які називаються рівняннями Гамільтона.
\[\frac{d \mathbb{M}}{d t} =-\frac{\partial H}{\partial x} \quad \text { and } \frac{d x}{d t} =\frac{\partial H}{\partial \mathbb{M}} \nonumber \]
Цей приклад узагальнено в табл\(\PageIndex{1}\). За аналогією з мовою, що використовується для опису схем та електромагнітів, зв'язок між узагальненим шляхом і узагальненим потенціалом називається конститутивною залежністю. Після рівняння 11.1.6 відношення узагальненого шляху до узагальненого потенціалу є узагальненою ємністю, а в даному прикладі - оберненою постійною пружини. Хоча зміщення\(x\) вважається скалярним, вектор\(\overrightarrow{x}\) використовується в таблиці для узагальненості.
| Пристрій накопичувача енергії | Лінійна пружина |
|---|---|
| Узагальнений шлях | Водотоннажність\(\overrightarrow{x}\) в м |
| Узагальнений потенціал | \(\overrightarrow{F}\)Сила в\(\frac{J}{m} = N\) |
| Узагальнена ємність | \(\frac{1}{K}\)в\(\frac{m^2}{J}\) |
| Конститутивні відносини | \(\overrightarrow{x} = \frac{1}{K}\overrightarrow{F}\) |
| Енергія | \(\frac{1}{2}\frac{1}{K}|\overrightarrow{x}|^2 = \frac{1}{2}K|\overrightarrow{F}|^2\) |
| Закон для потенціалу | Другий закон Ньютона\(\overrightarrow{F} = m\overrightarrow{a}\) |
