10.10: Взаємність

Термін «взаємність» відноситься до класу теорем, які пов'язують входи та виходи лінійної системи з тими, що мають однакову систему, в якій входи та виходи міняються місцями. Важливість взаємності в електромагнітиці полягає в тому, що вона спрощує проблеми, які в іншому випадку було б відносно важко вирішити. Прикладом цього є виведення приймальних властивостей антен, яке розглядається в інших розділах з використанням результатів, отриманих в цьому розділі.

Як початкове і відносно щадне введення розглянемо відомий особливий випадок, який виникає в базовій теорії схем: Двопортовий пристрій, показаний на малюнку\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\): Двопортовий пристрій. (суспільне надбання (модифіковане); Індуктивне навантаження)

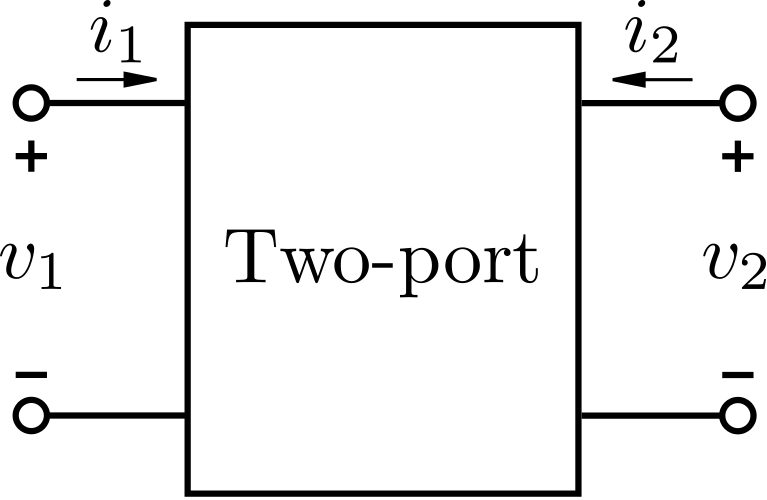
Двопортовий, як кажуть, є зворотним, якщо напруга,\(v_2\) що з'являється на порту 2 через струм, що подається на порт 1, така ж, як\(v_1\) при застосуванні того ж струму замість порту 2. Зазвичай це відбувається, коли двопортовий складається виключно з лінійних пасивних пристроїв, таких як ідеальні резистори, конденсатори та індуктори. Основною базовою вимогою є лінійність: Тобто виходи повинні бути пропорційними входам, а суперпозиція повинна застосовуватися.

Цей результат базової теорії схем насправді є окремим випадком більш загальної теореми електромагнітики, яку ми зараз виведемо. \(\PageIndex{2}\)На малюнку показано сценарій, в якому розподіл струму повністю\(\widetilde{\bf J}_1\) міститься в тому\(\mathcal{V}\).

Малюнок\(\PageIndex{2}\): Електромагнітна система, що складається з розподілу струму, що\(\widetilde{\mathbf{J}}_{1}\) випромінює електричне поле\(\widetilde{\mathbf{E}}_{1}\) в присутності лінійної речовини. (CC BY-SA 4.0; C Wang)

CC BY-SA 4.0

Цей струм виражається у вигляді об'ємної щільності струму, що має базові одиниці СІ А/м\(^2\). Також струм виражається в фазоровому вигляді, сигналізуючи про те, що ми розглядаємо єдину частоту. Цей розподіл струму породжує напруженість електричного поля\(\widetilde{\bf E}_1\), що має базові одиниці СІ В/м Об'єм може складатися з будь-якої комбінації лінійної інваріантної матерії; тобто діелектрична проникність\(\epsilon\)\(\mu\), проникність і провідність\(\sigma\) - це константи, які можуть змінюватися довільно з положенням, але не з часом.

Ось ключова ідея: ми можемо інтерпретувати цей сценарій як «двопортову» систему, в якій\(\widetilde{\bf J}_1\) є вхід,\(\widetilde{\bf E}_1\) є виходом, а поведінка системи повністю визначається рівняннями Максвелла в диференціальній фазорній формі:

\[\nabla \times \widetilde{\bf E}_1 = -j\omega\mu\widetilde{\bf H}_1 \label{m0214_eMCE1} \]

\[\nabla \times \widetilde{\bf H}_1 = \widetilde{\bf J}_1 + j\omega\epsilon\widetilde{\bf E}_1 \label{m0214_eMCH1} \]

поряд з відповідними електромагнітними граничними умовами. (Для цілей нашого теперішнього аналізу не\(\widetilde{\bf H}_1\) є ні входом, ні виходом; це просто зв'язана величина, яка з'являється в цій конкретній формулюванні взаємозв'язку між\(\widetilde{\bf E}_1\) і\(\widetilde{\bf J}_1\).)

Малюнок\(\PageIndex{3}\): Та сама електромагнітна система, як показано на малюнку\(\PageIndex{2}\) (включаючи однаковий розподіл речовини), але тепер з іншим входом\(widetilde{\mathbf{J}}_{2}\), що призводить до іншого виходу,\(widetilde{\mathbf{E}}_{2}\).

\(\PageIndex{3}\)На малюнку показаний сценарій, в якому інший розподіл струму повністю\(\widetilde{\bf J}_2\) міститься в одному об'ємі,\(\mathcal{V}\) що містить однаковий розподіл лінійної речовини. Цей новий розподіл струму породжує напруженість електричного поля\(\widetilde{\bf E}_2\). Взаємозв'язок між\(\widetilde{\bf E}_2\) і\(\widetilde{\bf J}_2\) регулюється одними і тими ж рівняннями:

\[\nabla \times \widetilde{\bf E}_2 = -j\omega\mu\widetilde{\bf H}_2 \label{m0214_eMCE2} \]

\[\nabla \times \widetilde{\bf H}_2 = \widetilde{\bf J}_2 + j\omega\epsilon\widetilde{\bf E}_2 \label{m0214_eMCH2} \]

поряд з тими ж електромагнітними граничними умовами. Таким чином, ми можемо інтерпретувати цей сценарій як ту саму електромагнітну систему\(\PageIndex{2}\), зображену на малюнку, за винятком тепер з\(\widetilde{\bf J}_2\) як вхід і\(\widetilde{\bf E}_2\) вихід.

Вхідний струм і вихідне поле в другому сценарії, як правило, повністю відрізняються від вхідного струму і вихідного поля в першому сценарії. Однак обидва сценарії включають в себе точно одну і ту ж електромагнітну систему; тобто однакові рівняння управління і однаковий розподіл речовини. Це призводить до наступного питання: Скажімо, ви нічого не знаєте про систему, окрім того, що вона лінійна та інваріантна. Однак ви в змозі спостерігати перший сценарій; тобто ви знаєте\(\widetilde{\bf E}_1\) у відповідь на\(\widetilde{\bf J}_1\). Враховуючи цей дуже обмежений погляд на поведінку системи, що ви можете зробити висновок про\(\widetilde{\bf E}_2\) даний\(\widetilde{\bf J}_2\), або навпаки? На перший погляд відповідь може здатися нічим, так як вам не вистачає опису системи. Однак відповідь виявляється, що дивно трохи більше інформації доступно. Ця інформація надається взаємністю. Щоб показати це, ми повинні займатися якоюсь чистою математикою.

Виведення теореми про взаємність Лоренца

Спочатку візьмемо точковий добуток\(\widetilde{\bf H}_2\) з кожної сторони рівняння\ ref {M0214_emce1}:

\[\widetilde{\bf H}_2 \cdot \left( \nabla \times \widetilde{\bf E}_1 \right) = -j\omega\mu\widetilde{\bf H}_1 \cdot \widetilde{\bf H}_2 \label{m0214_e5} \]

Аналогічно візьмемо точковий добуток\(\widetilde{\bf E}_1\) з кожної сторони Рівняння\ ref {M0214_EMCH2}:

\[\widetilde{\bf E}_1 \cdot \left( \nabla \times \widetilde{\bf H}_2 \right) = \widetilde{\bf E}_1 \cdot \widetilde{\bf J}_2 +j\omega\epsilon\widetilde{\bf E}_1 \cdot \widetilde{\bf E}_2 \label{m0214_e6} \]

Далі віднімемо Рівняння\ ref {m0214_e5} з рівняння\ ref {m0214_e6}. Ліва частина отриманого рівняння

\[\widetilde{\bf E}_1 \cdot \left( \nabla \times \widetilde{\bf H}_2 \right) - \widetilde{\bf H}_2 \cdot \left( \nabla \times \widetilde{\bf E}_1 \right) \nonumber \]

Це можна спростити за допомогою векторної ідентичності (Додаток 12.3):

\[\nabla \cdot \left({\bf A}\times {\bf B}\right) = {\bf B}\cdot\left(\nabla \times{\bf A}\right)-{\bf A}\cdot\left(\nabla \times{\bf B}\right) \nonumber \]

Врожайність

\[\widetilde{\bf E}_1 \cdot \left( \nabla \times \widetilde{\bf H}_2 \right) - \widetilde{\bf H}_2 \cdot \left( \nabla \times \widetilde{\bf E}_1 \right) = \nabla \cdot \left(\widetilde{\bf H}_2 \times \widetilde{\bf E}_1 \right) \nonumber \]

Отже, віднімаючи Рівняння\ ref {m0214_e5} з рівняння\ ref {m0214_e6}, ми знайшли:

\[\nabla \cdot \left(\widetilde{\bf H}_2 \times \widetilde{\bf E}_1 \right) = \widetilde{\bf E}_1 \cdot \widetilde{\bf J}_2 +j\omega\epsilon\widetilde{\bf E}_1 \cdot \widetilde{\bf E}_2 +j\omega\mu \widetilde{\bf H}_1 \cdot \widetilde{\bf H}_2 \label{m0214_e7} \]

Далі ми повторюємо процес, представлений рівняннями\ ref {m0214_e5} -\ ref {m0214_e7} вище, щоб створити додаткове рівняння до рівняння\ ref {m0214_e7}. Цього разу ми беремо крапковий\(\widetilde{\bf E}_2\) добуток з кожної сторони Рівняння\ ref {M0214_EMCH1}:

\[\widetilde{\bf E}_2 \cdot \left( \nabla \times \widetilde{\bf H}_1 \right) = \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 +j\omega\epsilon\widetilde{\bf E}_1 \cdot \widetilde{\bf E}_2 \label{m0214_e8} \]

Аналогічно візьмемо точковий добуток\(\widetilde{\bf H}_1\) з кожної сторони Рівняння\ ref {M0214_EMcE2}:

\[\widetilde{\bf H}_1 \cdot \left( \nabla \times \widetilde{\bf E}_2 \right) = -j\omega\mu\widetilde{\bf H}_1 \cdot \widetilde{\bf H}_2 \label{m0214_e9} \]

Далі віднімемо Рівняння\ ref {m0214_e9} з рівняння\ ref {m0214_e8}. Знову використовуючи векторну ідентичність, ліва частина отриманого рівняння

\[\widetilde{\bf E}_2 \cdot \left( \nabla \times \widetilde{\bf H}_1 \right) - \widetilde{\bf H}_1 \cdot \left( \nabla \times \widetilde{\bf E}_2 \right) = \nabla \cdot \left(\widetilde{\bf H}_1 \times \widetilde{\bf E}_2 \right) \nonumber \]

Так ми знаходимо:

\[\nabla \cdot \left(\widetilde{\bf H}_1 \times \widetilde{\bf E}_2 \right) = \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 +j\omega\epsilon\widetilde{\bf E}_1 \cdot \widetilde{\bf E}_2 +j\omega\mu \widetilde{\bf H}_1 \cdot \widetilde{\bf H}_2 \label{m0214_e10} \]

Нарешті, віднімаючи рівняння\ ref {m0214_e10} з рівняння\ ref {m0214_e7}, отримаємо:

\[\nabla \cdot \left(\widetilde{\bf H}_2 \times \widetilde{\bf E}_1 - \widetilde{\bf H}_1 \times \widetilde{\bf E}_2 \right) = \widetilde{\bf E}_1 \cdot \widetilde{\bf J}_2 - \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 \label{m0214_eLRTD} \]

Це рівняння широко відоме під назвою теореми, яку воно представляє: Теорема про взаємність Лоренца. Теорема є дуже загальним твердженням про взаємозв'язок між полями і струмами в кожній точці простору. Асоційована форма теореми застосовується до суміжних областей простору. Щоб отримати цю форму, ми просто інтегруємо обидві сторони Equation\ ref {M0214_elRTd} над томом\(\mathcal{V}\):

\ begin {вирівнювання}\ int_ {\ matchal V} {\ nabla\ dot\ ліворуч (\ widetilde {\ bf H} _2\ times\ widetilde {\ bf E} _1 -\ widetilde {\ bf E} _2\ number\ =\ int_ {\ mathcal V} {\ лівий (\ widetilde {\ bf E} _1\ cdot\ widetilde {\ bf J} _2 -\ widetilde {\ bf E} _2\ cdot\ widetilde {\ bf J} _1\ праворуч)} dv\ кінець { вирівняти}

Тепер ми зробимо додатковий крок використання теореми розбіжності (Додаток 12.3) для перетворення лівої частини рівняння в поверхневий інтеграл:

\ begin {вирівнювання}\ точка {\ matchal S} {\ лівий (\ widetilde {\ bf H} _2\ раз\ widetilde {\ bf E} _1 -\ widetilde {\ bf H} _1\ times\ widetilde {\ bf E} _2\ праворуч)\ cdot d {\ bf s}}\ nonumber\ =\ int_ {\ mathcal V} {\ лівий (\\ widetilde {\ bf E} _1\ dot\ widetilde {\ bf J} _2 -\ widetilde {\ bf E} _2\ dot\ widetilde {\ bf J} _1\ праворуч)} dv\ етикетка { m0214_ELRTI}\ кінець {вирівнювання}

де\(\mathcal{S}\) замкнута математична поверхня, яка межує\(\mathcal{V}\). Це також теорема про взаємність Лоренца, але тепер в інтегральній формі. Цей варіант теореми пов'язує поля на граничній поверхні з джерелами в межах об'єму.

Інтегральна форма теореми має особливо корисну особливість. Обмежимося джерелами кінцевою областю простору, дозволяючи при цьому\(\mathcal{V}\) рости нескінченно великим, розширюючись, включивши весь простір. У цій ситуації найближча відстань між будь-якою точкою, що містить ненульовий струм джерела і\(\mathcal{S}\) є нескінченним. Оскільки величина поля зменшується з відстанню від джерела, поля\((\widetilde{\bf E}_1,\widetilde{\bf H}_1)\) і\((\widetilde{\bf E}_2,\widetilde{\bf H}_2)\) всі фактично нульові\(\mathcal{S}\). У цьому випадку ліва частина Рівняння\ ref {M0214_ElRTi} дорівнює нулю, і знаходимо:

\[\boxed{ \int_{\mathcal V} {\left( \widetilde{\bf E}_1 \cdot \widetilde{\bf J}_2 - \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 \right)} dv = 0 } \label{m0214_eLRTI2} \]

для будь-якого обсягу\(\mathcal{V}\), який містить весь струм.

Теорема про взаємність Лоренца (Equation\ ref {M0214_ElrTi2}) описує зв'язок між одним розподілом струму і результуючими полями і другим розподілом поточного і результуючих полів, коли обидва сценарії відбуваються в однакових областях простору, заповнених однаковими розподіли лінійної матерії.

Чому ми називаємо ці відносини взаємністю? Просто тому, що вираз ідентичний, коли індекси «1» та «2» міняються місцями. Іншими словами, зв'язок не визнає відмінності між «входами» і «виходами»; є лише «порти».

Корисний особливий випадок стосується сценаріїв, в яких\(\widetilde{\bf J}_2\) поточні розподіли\(\widetilde{\bf J}_1\) і просторово незв'язані. Під «просторово незв'язаними» ми маємо на увазі, що немає точки в просторі, в якому обидва\(\widetilde{\bf J}_1\) і\(\widetilde{\bf J}_2\) є ненульовими; іншими словами, ці розподіли не перекриваються. (Зверніть увагу, що течії показані на малюнках\(\PageIndex{2}\) і\(\PageIndex{3}\) зображені як просторово нероз'єднані.) Щоб побачити, що відбувається в цьому випадку, давайте спочатку перепишемо Equation\ ref {M0214_elrti2} наступним чином:

\[\int_{\mathcal V} { \widetilde{\bf E}_1 \cdot \widetilde{\bf J}_2 ~dv } = \int_{\mathcal V} { \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 ~dv } \label{m0214_eLRTI3} \]

\(\mathcal{V}_1\)Дозволяти бути суміжний обсяг, над яким\(\widetilde{\bf J}_1\) ненульовий, і нехай\(\mathcal{V}_2\) бути суміжний обсяг, над яким\(\widetilde{\bf J}_2\) ненульовий. Тоді рівняння\ ref {M0214_ElrTi3} може бути записано наступним чином:

\[\int_{{\mathcal V}_2} { \widetilde{\bf E}_1 \cdot \widetilde{\bf J}_2 ~dv } = \int_{{\mathcal V}_1} { \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 ~dv } \label{m0214_eLRTI4} \]

Корисність цієї форми полягає в тому, що ми скоротили регіон інтеграції саме до тих регіонів, де існує течія.

Взаємність двох портів, що складаються з антен

Рівняння\ ref {M0214_ElrTi4} дозволяє встановити взаємність двох портів, що складаються з пар антен. Це найбільш легко продемонструвати для пар тонких дипольних антен, як показано на малюнку\(\PageIndex{4}\).

Малюнок\(\PageIndex{4}\): Двопортовий, що складається з двох дипольних антен. (CC BY-SA 4.0; C Wang)

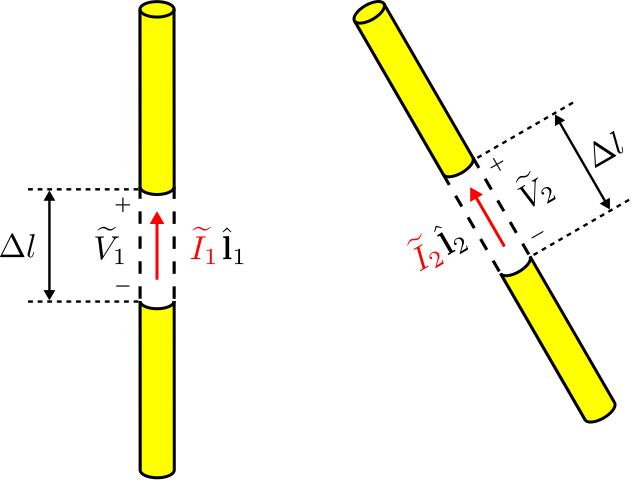
Тут порт 1 визначається термінальними\((\widetilde{V}_1,\widetilde{I}_1)\) величинами антени зліва, а порт 2 визначається термінальними\((\widetilde{V}_2,\widetilde{I}_2)\) величинами антени праворуч. Ці величини визначаються щодо невеликого зазору довжини\(\Delta l\) між ідеально провідними плечами диполя. Будь-яка антена може передавати або приймати, тому\((\widetilde{V}_1,\widetilde{I}_1)\) залежить від\((\widetilde{V}_2,\widetilde{I}_2)\), і навпаки.

Корпуси передачі та прийому для порту 1 проілюстровані на малюнку\(\PageIndex{5}\) (a) та (b) відповідно.

Малюнок\(\PageIndex{5}\): Антена порту 1 (а) передачі і (б) прийому. (CC BY-SA 4.0; C Wang)

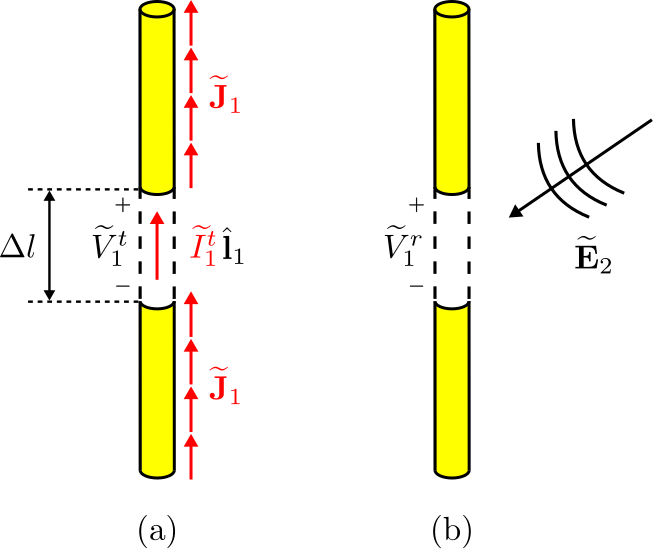
Зверніть увагу, що\(\widetilde{\bf J}_1\) це розподіл струму на цій антені при передачі (тобто, коли приводиться в рух струмом під впливом струму\(\widetilde{I}_1^t\)) і\(\widetilde{\bf E}_2\) електричне поле падає на антену, коли інша антена передає. Давайте\(\mathcal{V}_1\) виберемо циліндричний об'єм, який визначається зовнішньою поверхнею диполя, включаючи зазор між плечами диполя. Тепер ми готові розглянути праву частину Рівняння\ ref {M0214_ElrTi4}:

\[\int_{{\mathcal V}_1} { \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 ~dv } \nonumber \]

Електромагнітні граничні умови, застосовні до ідеально провідних дипольних плечей, дозволяють значно спростити цей інтеграл. По-перше, нагадаємо, що весь струм, пов'язаний з ідеальним провідником, повинен протікати по поверхні матеріалу, а значить\(\widetilde{\bf J}_1=0\) скрізь крім поверхні. Тому напрямок завжди\(\widetilde{\bf J}_1\) дотичне до поверхні. Дотична складова\(\widetilde{\bf E}_2\) дорівнює нулю на поверхні ідеально провідного матеріалу, як того вимагає застосовна гранична умова. Тому\(\widetilde{\bf E}_2\cdot\widetilde{\bf J}_1=0\) всюди\(\widetilde{\bf J}_1\) ненульовий.

Є лише одне місце, де струм ненульовий і все ж немає провідника: це місце - це зазор, розташований саме на клемах. Таким чином, знаходимо:

\[\int_{{\mathcal V}_1} { \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 ~dv} = \int_{gap} { \widetilde{\bf E}_2 \cdot \widetilde{I}_1^t \hat{\bf l}_1 ~dl } \nonumber \]

де права сторона - лінійний інтеграл, що перетинає зазор, який визначає клеми антени. Ми припускаємо, що струм\(\widetilde{I}_1^t\) є постійним над розривом, і тому може бути врахований з інтеграла:

\[\int_{{\mathcal V}_1} { \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 ~dv} = \widetilde{I}_1^t \int_{gap} { \widetilde{\bf E}_2 \cdot \hat{\bf l}_1 ~dl } \nonumber \]

Нагадаємо, що потенціал між двома точками в просторі задається інтегралом електричного поля по будь-якому шляху між цими двома точками. Зокрема, ми можемо розрахувати потенціал холостого ходу\(\widetilde{V}_1^r\) наступним чином:

\[\widetilde{V}_1^r = -\int_{gap} { \widetilde{\bf E}_2 \cdot \hat{\bf l}_1 ~dl } \nonumber \]

Примітно, що ми знайшли:

\[\int_{{\mathcal V}_1} { \widetilde{\bf E}_2 \cdot \widetilde{\bf J}_1 ~dv} = -\widetilde{I}_1^t \widetilde{V}_1^r \nonumber \]

Застосовуючи точно таку ж процедуру для порту 2 (або просто обмінюючись індексами), знаходимо:

\[\int_{{\mathcal V}_2} { \widetilde{\bf E}_1 \cdot \widetilde{\bf J}_2 ~dv} = -\widetilde{I}_2^t \widetilde{V}_2^r \nonumber \]

Тепер підставляючи ці результати в Equation\ ref {M0214_ElrTi4}, ми знаходимо:

\[\boxed{ \widetilde{I}_1^t \widetilde{V}_1^r = \widetilde{I}_2^t \widetilde{V}_2^r } \label{m0214_eRIV} \]

На початку цього розділу ми заявили, що двопортовий є зворотним, якщо\(\widetilde{V}_2\) з'являється в порту 2 через струм, застосований на порту 1, такий же, як і\(\widetilde{V}_1\) коли той же струм застосовується замість порту 2. Якщо справжня двухдипольная проблема є зворотною, то\(\widetilde{V}_2^r\) через\(\widetilde{I}_1^t\) повинна бути такою ж, як і\(\widetilde{V}_1^r\) коли\(\widetilde{I}_2^t=\widetilde{I}_1^t\). Це? Встановимо\(\widetilde{I}_1^t\) рівне якомусь певному значенню\(I_0\), тоді результуюче значення\(\widetilde{V}_2^r\) буде певним значенням\(V_0\). Якщо згодом встановити\(\widetilde{I}_2^t\) рівне\(I_0\), то отримане значення\(\widetilde{V}_1^r\) буде, відповідно до Equation\ ref {M0214_eRiv}:

\[\widetilde{V}_1^r = \frac{ \widetilde{I}_2^t \widetilde{V}_2^r }{ \widetilde{I}_1^t } = \frac{ I_0 V_0 }{ I_0 } = V_0 \nonumber \]

Тому Equation\ ref {M0214_eRiv} - це просто математична форма звичного визначення взаємності з базової теорії ланцюгів, і ми виявили, що наша система антен є зворотною саме в цьому ж сенсі.

Вищевказаний аналіз передбачав пари прямих, ідеально провідних диполів довільної довжини. Однак результат легко узагальнюється - насправді, однаковий - для будь-якої пари пасивних антен у лінійних інваріантних середовищах. Підводячи підсумки:

Потенціал, індукований на терміналах однієї антени через струм, застосований до другої антени, дорівнює потенціалу, індукованому в другій антені тим же струмом, що застосовується до першої антени (Equation\ ref {M0214_eRiv}).

Додаткове читання:

• «Взаємність (електромагнетизм)» у Вікіпедії.
• «Двопортова мережа» у Вікіпедії.