9.5: Випромінювання від електрично-короткого диполя

Найпростішим розподілом випромінюючого струму, яке зустрічається в звичайній практиці, є електрично-короткий диполь (ESD). Цей розподіл струму наведено на малюнку\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\): Розподіл струму електрично-короткого диполя (ESD). (CC BY-SA 4.0; C Wang)

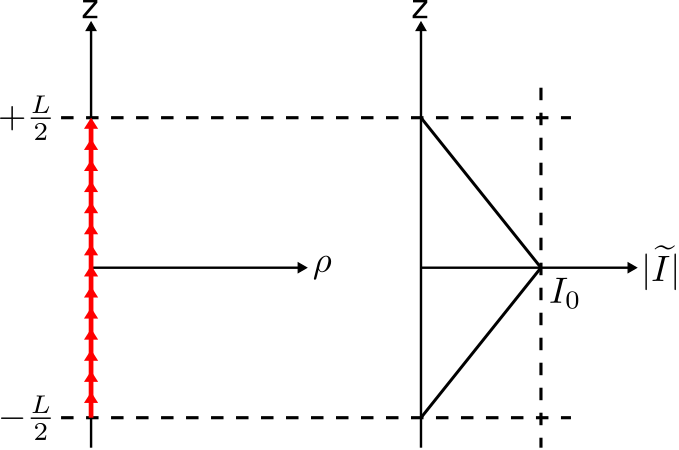
Дві характеристики, які визначають ESD, - це (1) струм вирівнюється по прямій лінії, і (2) довжина\(L\) лінії набагато менше половини довжини хвилі; тобто\(L\ll\lambda/2\). Остання характеристика - це те, що ми маємо на увазі під «електрично-коротким». ¹

Розподіл струму ОУР приблизно трикутний за величиною і приблизно постійний по фазі. Звідки ми це знаємо? По-перше, зауважте, що розподіли струму не можуть змінюватися складним або швидким шляхом на таких відстанях, які набагато менше довжини хвилі. Якщо це не відразу видно, нагадайте про поведінку ліній електропередачі: поточна стояча хвиля на лінії електропередачі демонструє період\(\lambda/2\), незалежно від джерела або припинення. Для ОУР,\(L\ll\lambda/2\) і тому ми очікуємо ще простішої варіації. Також ми знаємо, що струм на кінцях диполя повинен бути нулем, просто тому, що диполь там закінчується. Ці міркування означають, що нинішній розподіл ОУР добре наближений як трикутний за величиною. ² Виражається математично:

\[\widetilde{I}(z) \approx I_0 \left(1-\frac{2}{L}\left|z\right|\right) \nonumber \]

де\(I_0\) (СІ базові одиниці А) - складнозначна константа, яка вказує максимальну величину струму і фазу.

Є два підходи, які ми могли б розглянути, щоб знайти електричне поле, випромінюване ОУР. Перший підхід полягає в обчисленні потенціалу магнітного вектора\(\widetilde{\bf A}\) шляхом інтеграції над розподілом струму, обчислення і\(\widetilde{\bf H}=(1/\mu)\nabla\times\widetilde{\bf A}\), нарешті, обчислення\(\widetilde{\bf E}\) з\(\widetilde{\bf H}\) використанням закону Ампера. Ми будемо використовувати більш простий підхід, показаний на малюнку\(\PageIndex{2}\).

Малюнок\(\PageIndex{2}\): Розподіл струму електрично короткого диполя (ESD), наближеного як велика кількість диполів Герціана. (CC BY-SA 4.0; C Wang)

Уявіть собі ОУР як сукупність багатьох коротших сегментів струму, які випромінюють незалежно. Загальне поле - це сума цих коротких відрізків. Оскільки ці сегменти дуже короткі щодо довжини диполя, а також короткі щодо довжини хвилі, ми можемо наблизити струм над кожним сегментом як приблизно постійний. Іншими словами, ми можемо інтерпретувати кожен з цих сегментів як, до хорошого наближення, диполь Герца.

Перевага такого підходу полягає в тому, що у нас вже є рішення для кожного з сегментів. У розділі 9.4 показано, що\(\hat{\bf z}\) спрямований герціановий диполь біля початку випромінює електричне поле

\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j\eta \frac{\widetilde{I}\cdot\beta \Delta l}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \nonumber \]

де\(\widetilde{I}\) і\(\Delta l\) може інтерпретуватися як струм і довжина диполя відповідно. У цьому вираженні\(\eta\) є хвильовий опір середовища, в якому диполь випромінює (наприклад,\(\approx 377~\Omega\) для вільного простору), і ми припускаємо, що носії без втрат такі, що постійна ослаблення\(\alpha\approx 0\) та постійна поширення фази\(\beta=2\pi/\lambda\). Цей вираз також передбачає точки поля далеко від диполя; конкретно, відстані,\(r\) які набагато більше, ніж\(\lambda\). Перепрофілюючи цей вираз для цієї задачі, відрізок біля початку випромінює електричне поле:

\[\widetilde{\bf E}({\bf r};z'=0) \approx \hat{\bf \theta} j\eta \frac{I_0\cdot\beta \Delta l}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \nonumber \]

де позначення\(z'=0\) вказує на те, що герцианський диполь розташований біля початку. Дозволивши довжині\(\Delta l\) цього сегмента зменшуватися до диференціальної довжини\(dz'\), ми можемо описати внесок цього сегмента в поле, випромінюване ESD наступним чином:

\[d\widetilde{\bf E}({\bf r};z'=0) \approx \hat{\bf \theta} j\eta \frac{I_0\cdot\beta dz'}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \nonumber \]

Використовуючи такий підхід, електричне поле, випромінюване будь-яким сегментом, можна записати:

\[d\widetilde{\bf E}({\bf r};z') \approx \hat{\bf \theta}' j\eta\beta \frac{\widetilde{I}(z')}{4\pi}\left(\sin\theta'\right) \frac{e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|}}{\left|{\bf r}-\hat{\bf z}z'\right|}~dz' \nonumber \]

Зверніть увагу, що\(\theta\) замінюється\(\theta'\) так як промінь\({\bf r}-\hat{\bf z}z'\) утворює інший кут (тобто\(\theta'\)) по відношенню до\(\hat{\bf z}\). Аналогічно\(\hat{\bf \theta}\) замінюється на\(\hat{\bf \theta}'\), так як він також змінюється з\(z'\). Електричне поле, випромінюване ОУР, отримують шляхом інтеграції над цими внесками:

\[\widetilde{\bf E}({\bf r}) \approx \int_{-L/2}^{+L/2} d\widetilde{\bf E}(\hat{\bf r};z') \nonumber \]

врожайність:

\[\widetilde{\bf E}({\bf r}) \approx j \frac{\eta\beta}{4\pi} \int_{-L/2}^{+L/2} \hat{\bf \theta}' \widetilde{I}(z')~\left(\sin\theta'\right) \frac{e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|}}{\left|{\bf r}-\hat{\bf z}z'\right|} dz' \nonumber \]

З огляду на деякі припущення, які ми вже зробили, цей вираз можна ще більше спростити. Наприклад, зверніть увагу, що\(\theta'\approx\theta\) так як\(L\ll r\). З тієї ж причини,\(\hat{\bf \theta}'\approx\hat{\bf \theta}\). Оскільки ці змінні є приблизно постійними по довжині диполя, ми можемо перемістити їх за межі інтеграла, отримуючи:

\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \frac{\eta\beta}{4\pi}~\left(\sin\theta\right) \int_{-L/2}^{+L/2} \widetilde{I}(z') \frac{e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|}}{\left|{\bf r}-\hat{\bf z}z'\right|} dz' \label{m0198_eE1} \]

Також можна спростити вираз\(\left|{\bf r}-\hat{\bf z}z'\right|\). Розглянемо Малюнок\(\PageIndex{3}\).

Малюнок\(\PageIndex{3}\): Паралельне наближення променів для ОУР. (CC BY-SA 4.0; C Wang)

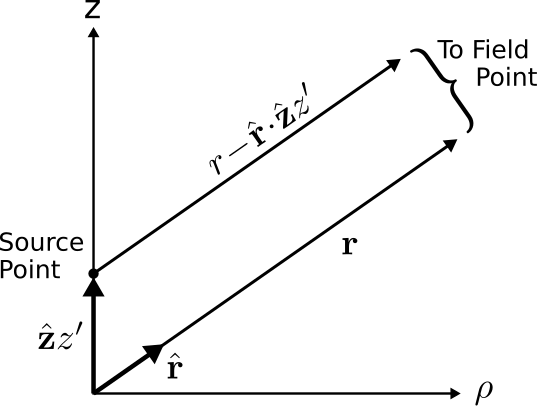
Оскільки ми вже припустили, що\(r\gg L\) (тобто відстань до точок поля набагато більше довжини диполя), вектор\({\bf r}\) приблизно паралельний вектору\({\bf r}-\hat{\bf z}z'\). Згодом, повинно бути правдою, що

\[\left|{\bf r}-\hat{\bf z}z'\right| \approx r-\hat{\bf r}\cdot\hat{\bf z}z' \label{m0198_ePRA} \]

Зверніть увагу, що величина\(r-\hat{\bf r}\cdot\hat{\bf z}z'\) повинна бути приблизно дорівнює\(r\), так як\(r\gg L\). Отже, наскільки\(\left|{\bf r}-\hat{\bf z}z'\right|\) визначає величину\(\widetilde{\bf E}({\bf r})\), ми можемо використовувати наближення:

\[\left|{\bf r}-\hat{\bf z}z'\right| \approx r ~~~\mbox{(magnitude)} \nonumber \]

Наскільки\(\left|{\bf r}-\hat{\bf z}z'\right|\) визначає фазу, ми повинні бути трохи обережнішими. Частина цілісного рівняння\ ref {M0198_EE1}, яка демонструє змінну фазу, є\(e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|}\). Використовуючи рівняння\ ref {m0198_epRa}, знаходимо

\[e^{-j\beta\left|{\bf r}-\hat{\bf z}z'\right|} \approx e^{-j\beta r} e^{+j\beta\hat{\bf r}\cdot\hat{\bf z}z'} \nonumber \]

Найгірший випадок з точки зору зміни фази всередині інтеграла - для точок поля вздовж\(z\) осі. Для цих точок\(\hat{\bf r}\cdot\hat{\bf z}=\pm 1\) і згодом\(\left|{\bf r}-\hat{\bf z}z'\right|\) змінюється від\(z-L/2\) того,\(z+L/2\) де\(z\) знаходиться місце розташування польової точки. Однак, оскільки\(L\ll\lambda\) (тобто тому, що диполь електрично короткий), ця різниця в довжині набагато менше\(\lambda/2\). Тому фаза\(\beta \hat{\bf r}\cdot\hat{\bf z}z'\) змінюється набагато менше, ніж\(\pi\) радіани, а згодом\(e^{-j\beta\hat{\bf r}\cdot\hat{\bf z}z'}\approx 1\). Ми робимо висновок, що за цих умов

\[e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|} \approx e^{-j\beta r} ~~~\mbox{(phase)} \nonumber \]

Застосовуючи ці спрощення для величини та фази до рівняння\ ref {m0198_ee1}, отримаємо:

\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \frac{\eta\beta}{4\pi} \left(\sin\theta\right) \frac{e^{-j\beta r}}{r}~\int_{-L/2}^{+L/2} \widetilde{I}(z') dz' \nonumber \]

Інтеграл в цьому рівнянні оцінити дуже легко; насправді з огляду (рис.\(\PageIndex{1}\)) ми визначаємо, що він дорівнює\(I_0L/2\). Нарешті, отримуємо:

\[\boxed{ \widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \eta \frac{I_0\cdot\beta L}{8\pi} ~\left(\sin\theta\right) ~\frac{e^{-j\beta r}}{r} } \label{m0198_eESDE} \]

Підводячи підсумки:

Напруженість електричного поля, випромінюваного ОУР, розташованим у початку та вирівняним вздовж\(z\) осі, задається Equation\ ref {M0198_EESDE}. Цей вираз справедливо для\(r\gg\lambda\).

Варто зазначити, що зміна величини, фази та поляризації ОУР з розташуванням точки поля ідентична коливанню одного диполя Герціана, що має струмовий момент\(\hat{\bf z} I_0 L/2\) (розділ 9.4). Однак величина поля, випромінюваного ОУР, становить рівно половину від герцианського диполя. Чому одна половина? Просто тому, що інтеграл над трикутним розподілом струму, передбачуваним для ESD, є половиною інтеграла над рівномірним розподілом струму, який визначає диполь Герца. Це аналогічно іноді викликає плутанину між герцианськими диполями та ESD. Пам'ятайте, що ESD є фізично реалізованими, тоді як герцианські диполі - ні.

Загальноприйнятим є усунення коефіцієнта величини\(\beta\) за допомогою співвідношення\(\beta=2\pi/\lambda\), поступаючись:

\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \frac{\eta I_0}{4} \frac{L}{\lambda} ~\left(\sin\theta\right) ~\frac{e^{-j\beta r}}{r} \nonumber \]

У\(r\gg\lambda\) польових точках хвиля виявляється локально плоскою. Тому ми виправдовуємо використання плоского хвильового співвідношення\(\widetilde{\bf H} = \frac{1}{\eta} \hat{\bf r} \times \widetilde{\bf E}\) для обчислення\(\widetilde{\bf H}\). В результаті виходить:

\[\widetilde{\bf H}({\bf r}) \approx \hat{\bf \phi} j \frac{I_0}{4} \frac{L}{\lambda} ~\left(\sin\theta\right) ~\frac{e^{-j\beta r}}{r} \label{m0198_eESDH} \]

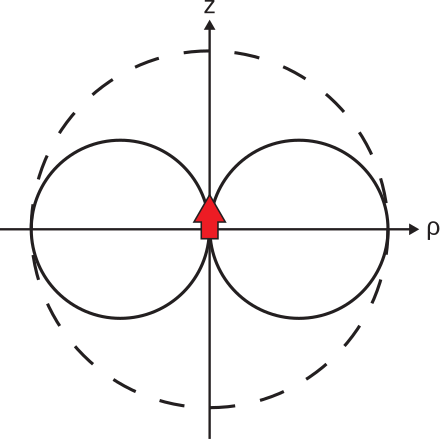
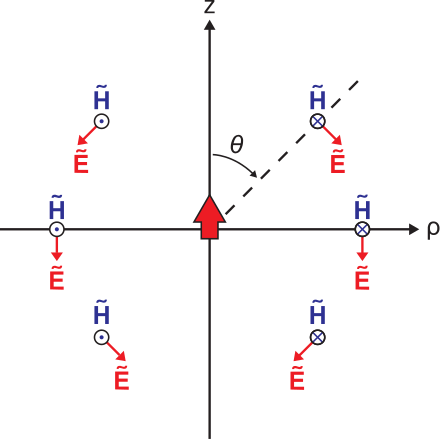
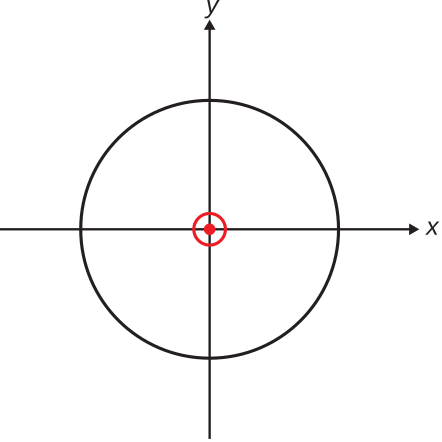
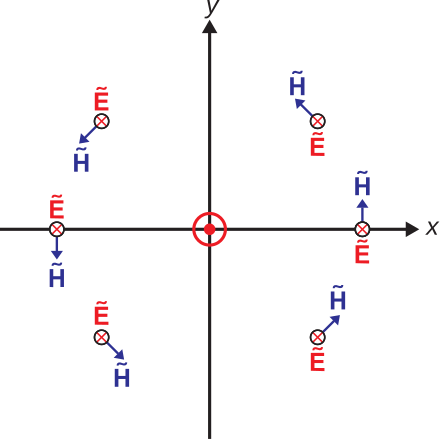
Наостанок розглянемо просторові характеристики випромінюваного поля. Цифри\(\PageIndex{4}\) і\(\PageIndex{5}\) показують результат в площині постійної\(\phi\). Цифри\(\PageIndex{6}\) і\(\PageIndex{7}\) показують результат в\(z=0\) площині. Зверніть увагу, що орієнтації векторів електричного та магнітного поля вказують на вектор Пойнтінга\(\widetilde{\bf E}\times\widetilde{\bf H}\), який завжди спрямований радіально назовні від місця розташування диполя. Це підтверджує, що потік потужності завжди спрямований радіально назовні від диполя. Завдяки симетрії задачі, фігури\(\PageIndex{4}\) —\(\PageIndex{7}\) дають повну характеристику відносних величин і орієнтацій випромінюваних полів.

Малюнок\(\PageIndex{4}\): Величина випромінюваного поля в будь-якій площині постійної\(\phi\). (CC BY-SA 4.0; С.Лаллі)

Рисунок\(\PageIndex{5}\): Орієнтація електричного і магнітного полів в будь-якій площині постійної\(\phi\). (CC BY-SA 4.0; С.Лаллі)

Малюнок\(\PageIndex{6}\): Величина випромінюваного поля в будь-якій площині постійної\(z\). (CC BY-SA 4.0; С.Лаллі)

Малюнок\(\PageIndex{7}\): Орієнтація електричного та магнітного полів у\(z=0\) площині (CC BY-SA 4.0; С.Лаллі)

---

1. Потенційним джерелом плутанини є те, що диполь Герца також є «диполем», який є «електрично-коротким». Відмінність полягає в тому, що струм, що містить диполь Герца, є постійним по всій довжині. Ця умова рідко і лише приблизно спостерігається на практиці, тоді як розподіл трикутної величини є відносно хорошим наближенням до широкого класу поширених електрично-коротких дротяних антен. Таким чином, термін «електрично-короткий диполь», як використовується в цій книзі, відноситься до трикутного розподілу, якщо не зазначено інше. ↩
2. Більш суворий аналіз, що призводить до такого ж висновку, можливий, але виходить за рамки цієї книги. ↩