3.5: Трифазні трансформатори

Трифазний трансформатор - це просто три однофазних трансформатора. Ускладнення в цих речах полягає в тому, що існує ряд способів їх намотування, і ряд способів їх з'єднання між собою. Про обмотки нам доведеться більше сказати пізніше. Поки розглянемо взаємозв'язки. З будь-якої «сторони» трансформаторного з'єднання (тобто з боку високої напруги та низької напруги) можна підключати обмотки трансформатора або лінію до нейтралі (wye), або лінію до лінії (дельта). Таким чином, ми можемо говорити про трансформаторних з'єднаннях, що є вій-вей, дельта-дельта, бай-дельта, або дельта-вей.

Ігноруючи певні ускладнення, про які нам доведеться більше сказати найближчим часом, підключення трансформаторів будь-яким способом або дельта-дельтою досить легко зрозуміти. Кожне з лінійно-нейтральних (у випадку wye-wye), або лінійно-лінійне (у випадку дельта-дельта) напруг перетворюється одним з трьох трансформаторів. З іншого боку, взаємозв'язки трансформатора «бай-дельта» або «дельта» трохи складніші. На малюнку 16 показано з'єднання дельта, у тому, що може називатися «схемою підключення». Більш схематична (і більш поширена) форма того ж малюнка показана на малюнку 17. На цьому малюнку елементи обмотки, які здаються паралельними, намотані на один і той же сегмент сердечника, і тому складають однофазний трансформатор.

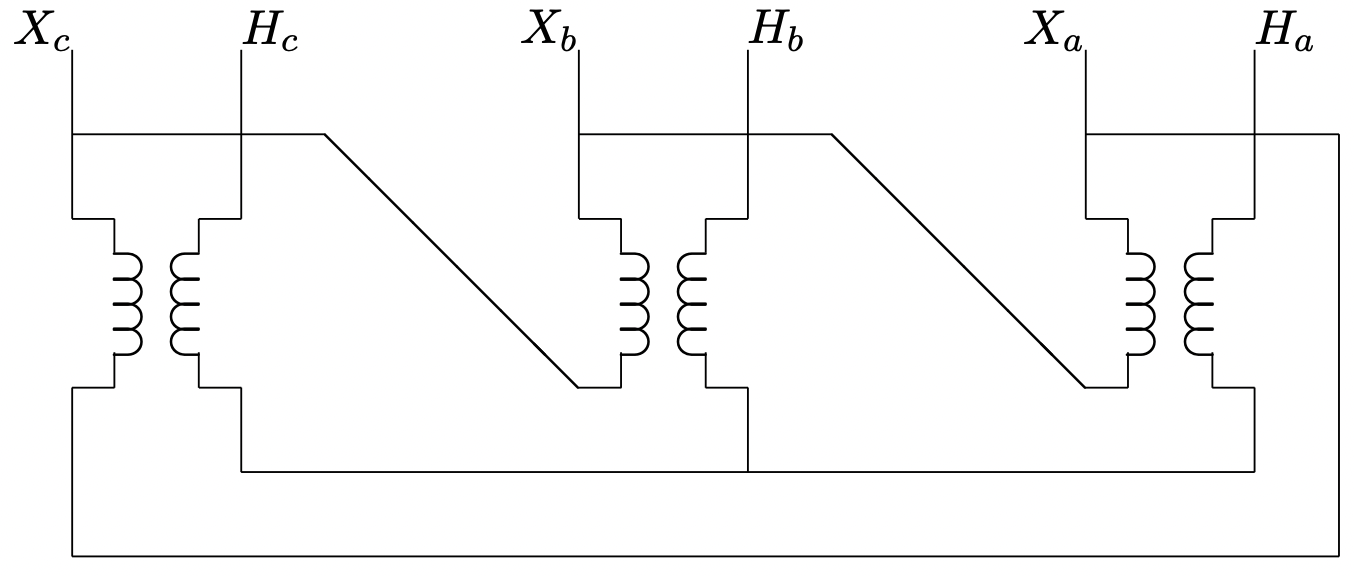Малюнок 16: Підключення трансформатора Delta-Wye

Тепер: припустимо, що\(\ N_{\Delta}\) і\(\ N_{Y}\) є номерами витків. Якщо окремі трансформатори вважаються ідеальними, існують такі обмеження напруги і струму:

\[\ v_{a Y}=\frac{N_{Y}}{N_{\Delta}}\left(v_{a \Delta}-v_{b \Delta}\right)\label{37} \]

\[\ v_{b Y}=\frac{N_{Y}}{N_{\Delta}}\left(v_{b \Delta}-v_{c \Delta}\right)\label{38} \]

\[\ v_{c Y}=\frac{N_{Y}}{N_{\Delta}}\left(v_{c \Delta}-v_{a \Delta}\right)\label{39} \]

\[\ i_{a \Delta}=\frac{N_{Y}}{N_{\Delta}}\left(i_{a Y}-i_{c Y}\right)\label{40} \]

\[\ i_{b \Delta}=\frac{N_{Y}}{N_{\Delta}}\left(i_{b Y}-i_{a Y}\right)\label{41} \]

\[\ i_{c \Delta}=\frac{N_{Y}}{N_{\Delta}}\left(i_{c Y}-i_{b Y}\right)\label{42} \]

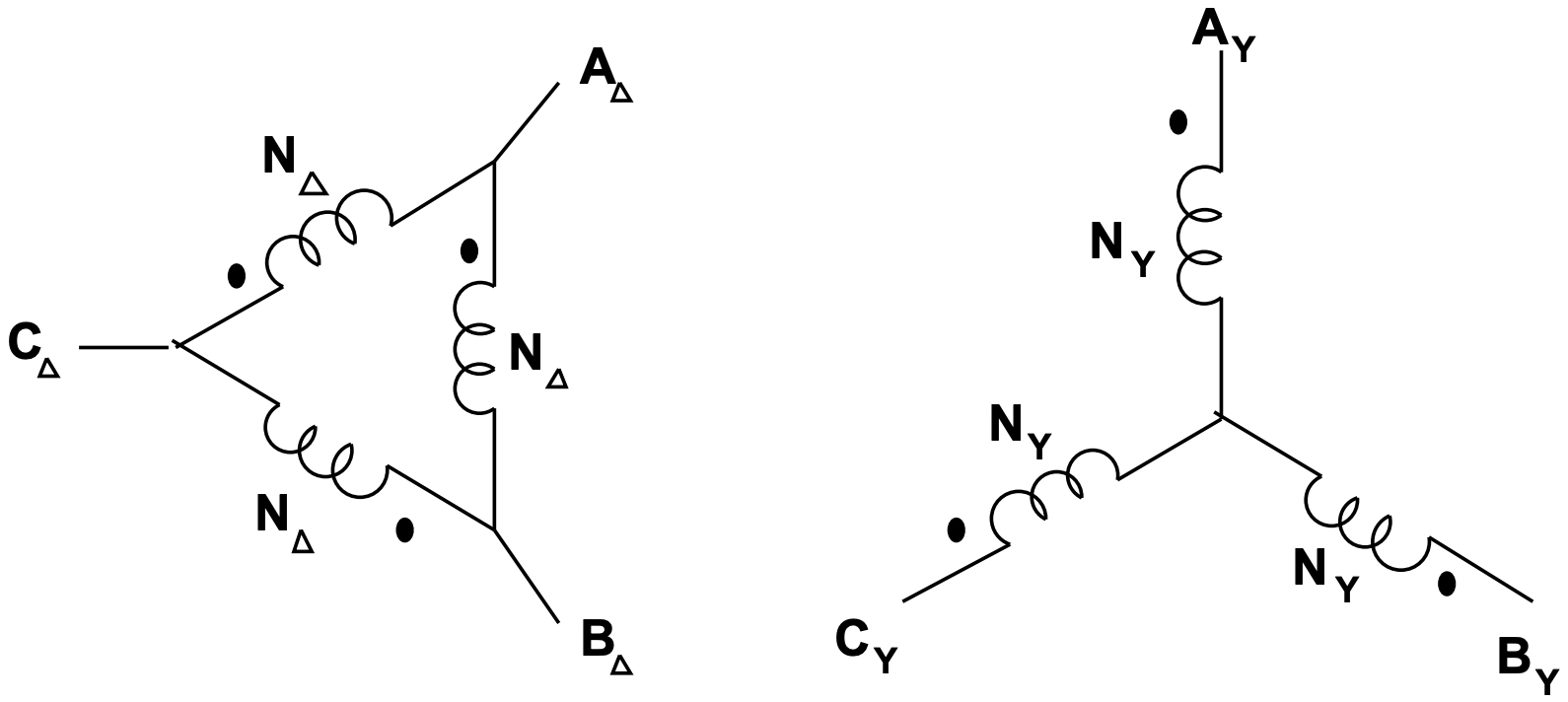Малюнок 17: Схема з'єднання трансформатора Delta-Wye

де кожне з напруг лінійно-нейтральне і струми знаходяться в лініях на клемах трансформатора.

Тепер розглянемо, що буде, якщо\(\ \Delta-Y\) трансформатор підключений до збалансованого трифазного джерела напруги, щоб:

\ (\\ begin {масив} {l}
v_ {a\ Delta} =R е\ лівий (\ підкреслення {V} e^ {j\ omega t}\ праворуч)\\
v_ {b\ Delta} =\ ім'я оператора {Re}\ лівий (\ підкреслення {V} e^ {j\ лівий (\ омега t-\ frac {2\ pi} {3}\ праворуч)\ праворуч)\\
v_ {c\ Delta} =\ ім'я оператора {Re}\ ліворуч (\ підкреслення {V} e^ {j\ left (\ омега t+\ frac {2\ pi} {3} \ право)}\ право)
\ end {масив}\)

Тоді комплексними амплітудами\(\ wye\) збоку є:

\ (\\ begin {масив} {ll}
\ підкреслення {V} _ {a Y} = &\ frac {N_ {Y}} {N {\ Дельта}}\ підкреслення {V}\ лівий (1-e^ {-j\ frac {2\ pi} {3}}\ правий) = &\ sqrt {3}\ frac {N_ {Y}} {N _}\ Дельта}}\ підкреслення {V} e^ {j\ frac {\ pi} {\ pi} {6}}
\\ підкреслення {V} _ {b Y} = &\ frac {N_ {Y}} {N_ {\ Delta}}\ підкреслення {V}\ ліворуч (e^ {-j\ гідророзриву {2\ pi} {3}} -e^ {j\ frac {2\ pi} {3}}\ право) = &\ sqrt {3}\ frac {N {Y}} {N {\ Дельта}}\ підкреслення {V} e^ {-j\ frac {\ pi} {2}}\
\ підкреслення {V} _ {C} = &\ frac {N_ {Y}} {N_ {\ Дельта}}\ підкреслення {V}\ ліворуч (e^ {j\ frac {2\ pi} {3}} -1\ праворуч) = &\ sqrt {3}\ frac {N_ {Y}} {N_ {\ Delta}}\ підкреслення {V} e^ {j\ frac {5\ pi} { 6}}
\ end {масив}\)

Тут слід зробити два зауваження:

• Відношення напруг (тобто відношення або лінія-лінія, або лінія-нейтраль) відрізняється від коефіцієнта витків на коефіцієнт\(\ \sqrt{3}\).
• Всі\(\ wye\) бічні напруги зміщені по фазі на 30 ^о щодо дельта-бічних напруг.

Приклад

Припустимо, у нас є наступна проблема для вирішення:

\(\ \Delta\)Збоку\(\ Y-\Delta\) трансформатора з'єднаний збалансований трифазний резистор з номінальним співвідношенням напруги

\(\ \frac{v_{\Delta}}{v_{Y}}=N\)

Який імпеданс дивиться в сторону ока трансформатора, припускаючи привід з збалансованим джерелом?

Ситуація показана на малюнку 18.

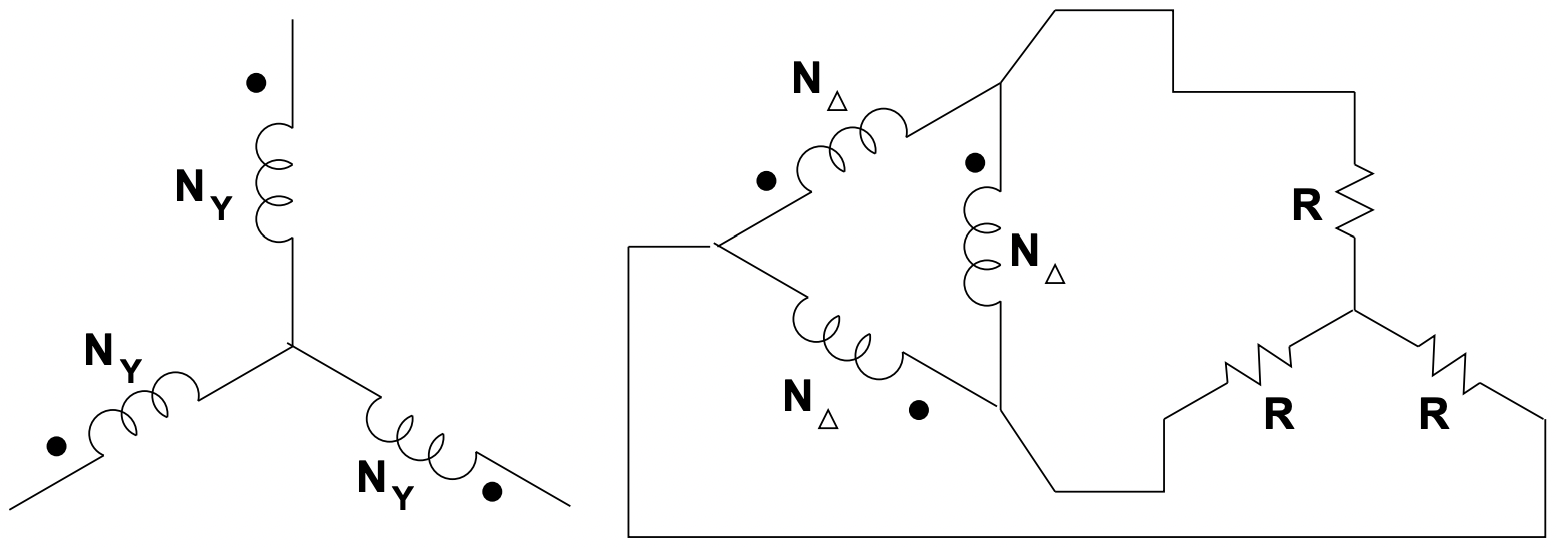Малюнок 18: Приклад

Важливо пам'ятати про взаємозв'язок між коефіцієнтом напруги і коефіцієнтом витків, яке становить:

\(\ \frac{v_{\Delta}}{v_{Y}}=N=\frac{N_{\Delta}}{\sqrt{3} N_{Y}}\)

так що:

\(\ \frac{N_{\delta}}{N_{Y}}=\frac{N}{\sqrt{3}}\)

Далі\(\ Y-\Delta\) еквівалентне перетворення для навантаження робить картинку схожою на цифру 19

У цій ситуації кожна вторинна обмотка трансформатора підключається безпосередньо через один з трьох резисторів. Струми в резисторах задаються:

\ (\\ почати {вирівняний}
i_ {1} &=\ розриву {v_ {a b\ Delta}} {3 R}\\
i_ {2} &=\ розриву {v_ {b c\ Delta}} {3 R}\\
i_ {3} &=\ frac {v_ {c a\ Delta}} {3 R}
\ кінець {вирівняний}\)

Лінійні струми бувають:

\ (\\ почати {вирівняний}
i_ {a\ Delta} =& i_ {1} -i_ {3} =\ розриву {v_ {a b\ Delta} -v_ {c a\ Дельта}} {3 R} =i_ {1\ Дельта} -i_ {3\ Дельта}\
i_ {b\ Дельта} =& i_ {2} -i_ {1} =\ гідророзриву {v_ {b c\ Дельта} -v_ {a b\ Delta}} {3 R} =i_ {2\ Дельта} -i_ {1\ Дельта}\\
i_ {c\ Дельта} =& i_ {3} -i_ {2} =\ гідророзриву {v_ {c a\ Дельта} -v_ {b c\ Дельта}} {3 R} =i_ {3\ Дельта} -i_ {2\ Дельта}
\ кінець {вирівняний}\)

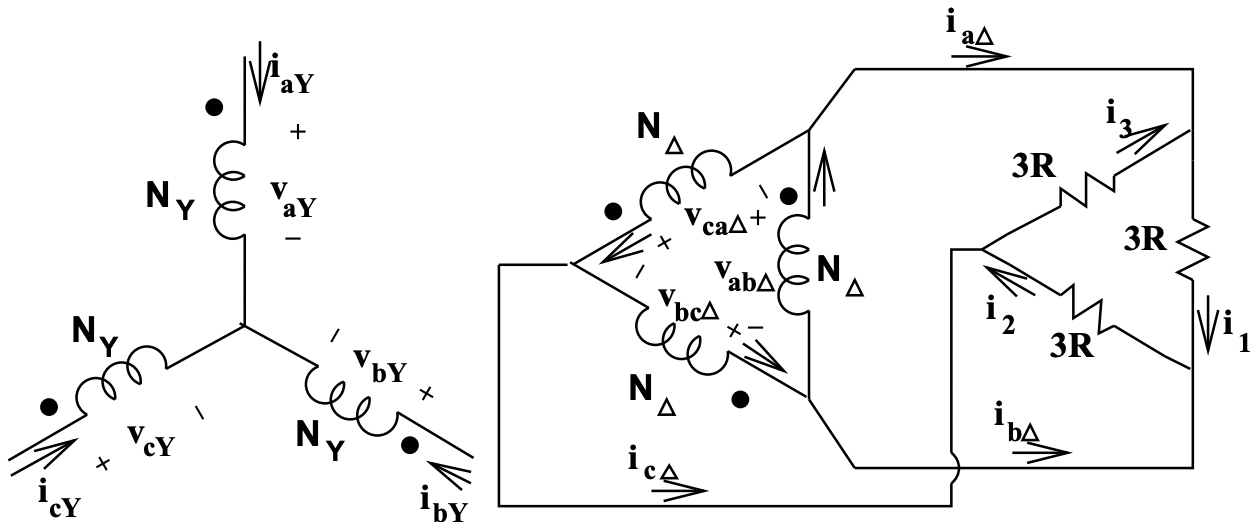Малюнок 19: Еквівалентна ситуація

Вирішуючи для струмів в ніжках трансформатора\(\ \Delta\), відніміть, наприклад, другий вираз з першого:

\(\ 2 i_{1 \Delta}-i_{2 \Delta}-i_{3 \Delta}=\frac{2 v_{a b \Delta}-v_{b c \Delta}-v_{c a \Delta}}{3 R}\)

Тепер, скориставшись тим, що система збалансована:

\ (\\ begin {масив} {r}
i_ {1\ Дельта} +i_ {2\ Дельта} +i_ {3\ Дельта} =0\
v_ {a b\ Delta} +v_ {b c\ Delta} +v_ {c a\ Delta} =0
\ end {масив}\)

знайти:

\ (\\ begin {масив} {l}
i_ {1\ Дельта} =\ гідророзриву {v_ {a b\ Delta}} {3 R}\
i_ {2\ Дельта} =\ frac {v_ {b c\ Delta}} {3 R}\
i_ {3\ Дельта} =\ frac {v_ {c a\ Delta}} {3 R}
\ кінець масиву {}\)

Нарешті, ідеальні трансформаторні відносини дають:

\ (\\ begin {масив} {ll}
v_ {a b\ Delta} =\ гідророзриву {N_ {\ Дельта}} {N _ {Y}} v_ {a Y} & i_ {a Y} =\ frac {\ Дельта}} {N_ {Y}} i_ {1\ Дельта}\
v_ {b c\ Delta} =\ frac {N_ {N _ {\ Дельта}} {N_ {Y}} v_ {b Y} & i_ {b Y} =\ гідророзриву {N_ {\ Дельта}} {N_ {Y}} i_ {2\ Дельта}\\
v_ {c a\ Delta} =\ frac {N_ {\ Дельта}} {N {Y}} v _ {c Y} & i_ {c Y} =\ розрив {N_ {\ Дельта}} {N_ {Y}} i_ {3\ Дельта}
\ кінець {масив}\)

так що:

\ (\\ почати {вирівняний}
i_ {A Y} &=\ лівий (\ розриву {N_ {\ Delta}}} {N {Y}\ праворуч) ^ {2}\ frac {1} {3 R} v_ {a Y}\\
i_ {b Y} &=\ лівий (\ frac {N_ {\ Дельта}} {N} {Y}\ праворуч) ^ {2}\ гідророзриву {1} {3 R} v_ {b Y}\\
i_ {c Y} &=\ лівий (\ гідророзриву {N_ {\ Дельта}} {N {Y}}\ праворуч) ^ {2}\ frac {1} {3 R} v_ {c Y}
\ end {вирівняний}\)

Видимий опір (тобто видиме, чи слід його підключати\(\ wye\)) на\(\ wye\) клемах трансформатора становить:

\(\ R_{e q}=3 R\left(\frac{N_{Y}}{N_{\Delta}}\right)^{2}\)

Виражається в перерахунку на коефіцієнт напруги, це:

\(\ R_{e q}=3 R\left(\frac{N}{\sqrt{3}}\right)^{2}=R\left(\frac{v_{Y}}{v_{\Delta}}\right)^{2}\)

Важливо відзначити, що це рішення зайняло довгий шлях. Взяті послідовно (рівномірно на лінійній нейтралі або рівномірно на лінійній основі), імпеданси трансформуються через трансформатори квадратом коефіцієнта напруги, незалежно від того, яке з'єднання використовується.