3.2: Трифазні системи

Тепер розглянемо розташування трьох джерел напруги, проілюстроване на малюнку 3.

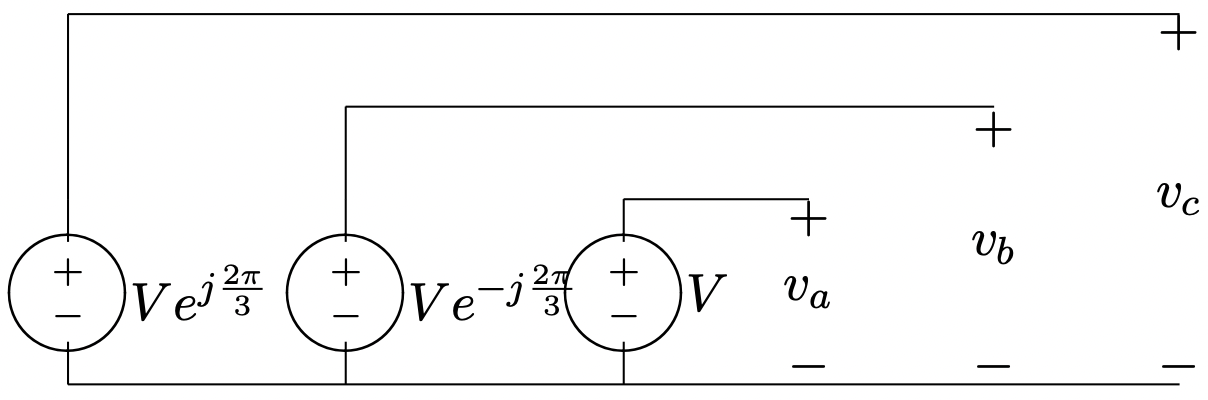Малюнок 3: Трифазне джерело напруги

Трифазні напруги бувають:

$$\ v_{a}=\quad V \cos \omega t \quad=R e\left[V e^{j \omega t}\right]\label{9}$$

$$\ v_{b}=V \cos \left(\omega t-\frac{2 \pi}{3}\right)=R e\left[V e^{j\left(\omega t-\frac{2 \pi}{3}\right)}\right]\label{10}$$

$$\ v_{c}=V \cos \left(\omega t+\frac{2 \pi}{3}\right)=\operatorname{Re}\left[V e^{j\left(\omega t+\frac{2 \pi}{3}\right)}\right]\label{11}$$

Ці трифазні напруги проілюстровані в часовій області на малюнку 4 і як складні фазори на малюнку 5. Зверніть увагу на симетричний інтервал у часі напруг. Як і в попередніх прикладах, миттєві напруги можна візуалізувати, уявивши малюнок 5, що обертається проти годинникової стрілки з кутовою швидкістю$\ \omega$. Миттєві напруги - це всього лише проекції векторів цієї «вертушки» на горизонтальну вісь.

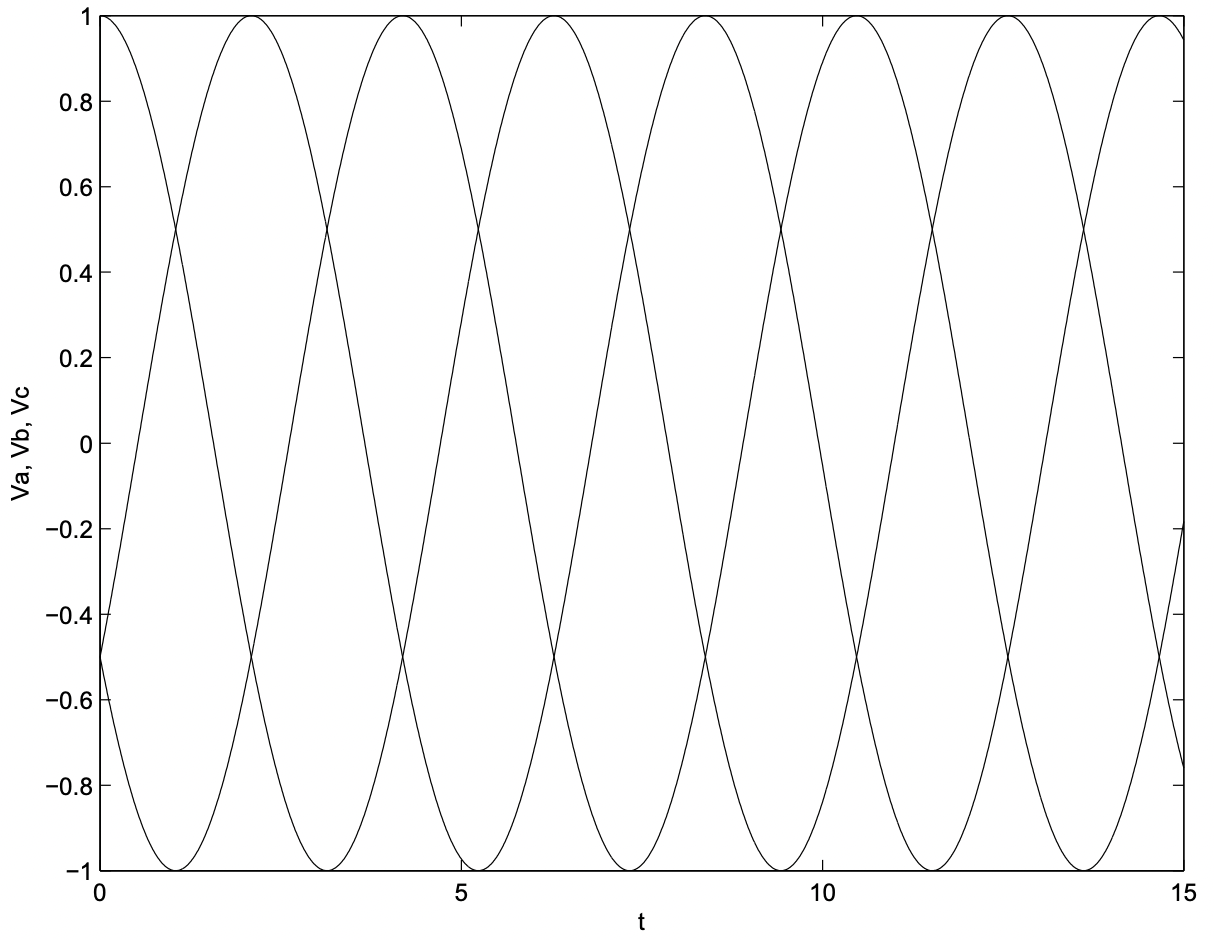Малюнок 4: Трифазні напруги

Розглянемо підключення цих трьох джерел напруги до трьох однакових навантажень, кожна зі складним опором$\ \underline{Z}$, як показано на малюнку 6.

Якщо напруги вказані (9 - 11), то струми в трьох фазах бувають:

$$\ i_{a}=R e\left[\frac{\underline{\underline{V}}}{\underline{Z}} e^{j \omega t}\right]\label{12}$$

$$\ i_{b}=\operatorname{Re}\left[\frac{\underline{V}}{\underline{Z}} e^{j\left(\omega t-\frac{2 \pi}{3}\right)}\right]\label{13}$$

$$\ i_{c}=R e\left[\frac{\underline{V}}{\underline{Z}} e^{j\left(\omega t+\frac{2 \pi}{3}\right)}\right]\label{14}$$

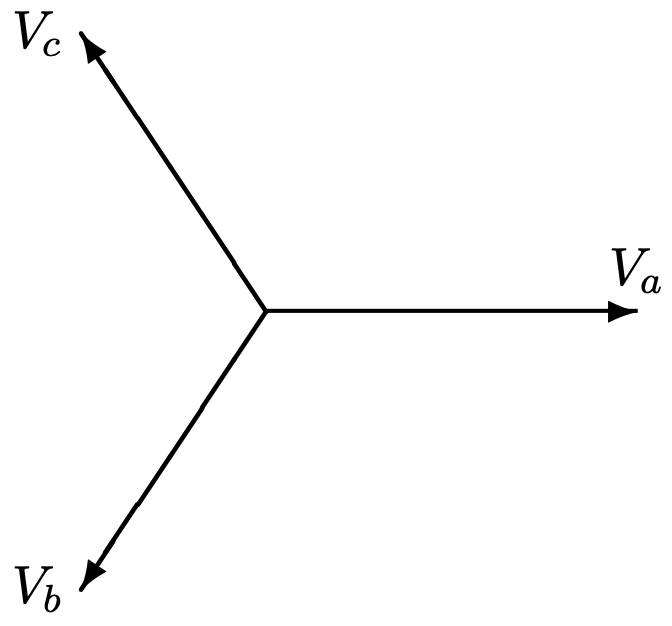Малюнок 5: Фазорна діаграма: Трифазні напруги

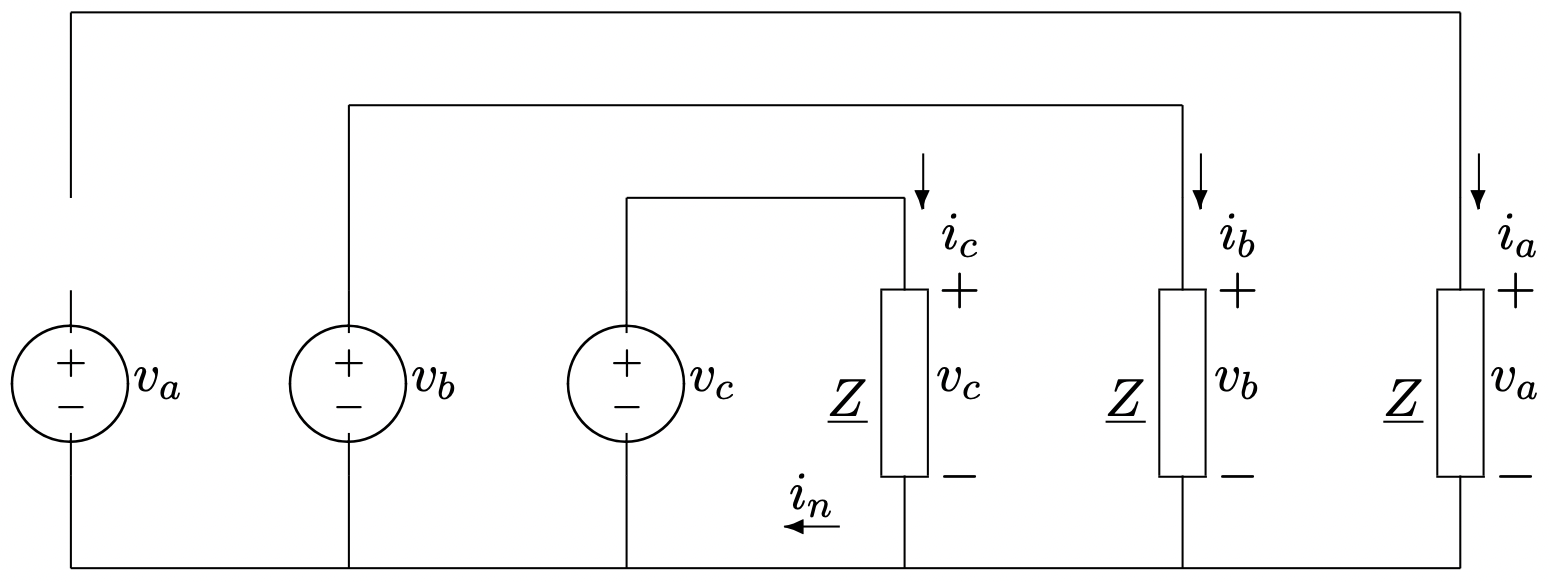Малюнок 6: Трифазне джерело, підключене до збалансованого навантаження

Комплексна потужність в кожній з трьох фаз становить:

$$\ P+j Q=\frac{|\underline{V}|^{2}}{2|\underline{Z}|}(\cos \psi+j \sin \psi)\label{15}$$

Потім, запам'ятовуючи часову фазу трьох джерел, можна записати значення миттєвої потужності в три фази:

$$\ p_{a}=\frac{|\underline{V}|^{2}}{2|\underline{Z}|}\{\cos \psi[1+\cos 2 \omega t]+\sin \psi \sin 2 \omega t\}\label{16}$$

$$\ p_{b}=\frac{|\underline{V}|^{2}}{2|\underline{Z}|}\left\{\cos \psi\left[1+\cos \left(2 \omega t-\frac{2 \pi}{3}\right)\right]+\sin \psi \sin \left(2 \omega t-\frac{2 \pi}{3}\right)\right\}\label{17}$$

$$\ p_{c}=\frac{|\underline{V}|^{2}}{2|\underline{Z}|}\left\{\cos \psi\left[1+\cos \left(2 \omega t+\frac{2 \pi}{3}\right)\right]+\sin \psi \sin \left(2 \omega t+\frac{2 \pi}{3}\right)\right\}\label{18}$$

Сума цих трьох виразів - сумарна миттєва потужність, яка є постійною:

$$\ p=p_{a}+p_{b}+p_{c}=\frac{3}{2} \frac{|\underline{V}|^{2}}{|\underline{Z}|} \cos \psi\label{19}$$

Корисно при роботі з трифазними системами пам'ятати, що

$\ \cos x+\cos \left(x-\frac{2 \pi}{3}\right)+\cos \left(x+\frac{2 \pi}{3}\right)=0$

незалежно від величини$\ x$.

Тепер розглянемо струм в нульовому проводі,$\ i_{n}$ на малюнку 6. Цей струм задається:

$$\ i_{n}=i_{a}+i_{b}+i_{c}=R e\left[\frac{V}{\underline{Z}}\left(e^{j \omega t}+e^{j\left(\omega t-\frac{2 \pi}{3}\right)}+e^{j\left(\omega t+\frac{2 \pi}{3}\right)}\right)\right]=0\label{20}$$

Це показує найважливішу перевагу трифазних систем перед двофазними системами: провід без струму в ньому не обов'язково повинен бути дуже великим. Насправді нейтральне з'єднання може бути повністю усунуто у багатьох випадках. Мережа, показана на малюнку 7, буде працювати так само, як і мережа на малюнку 6 в більшості випадків, в яких напруги і опори навантаження збалансовані.

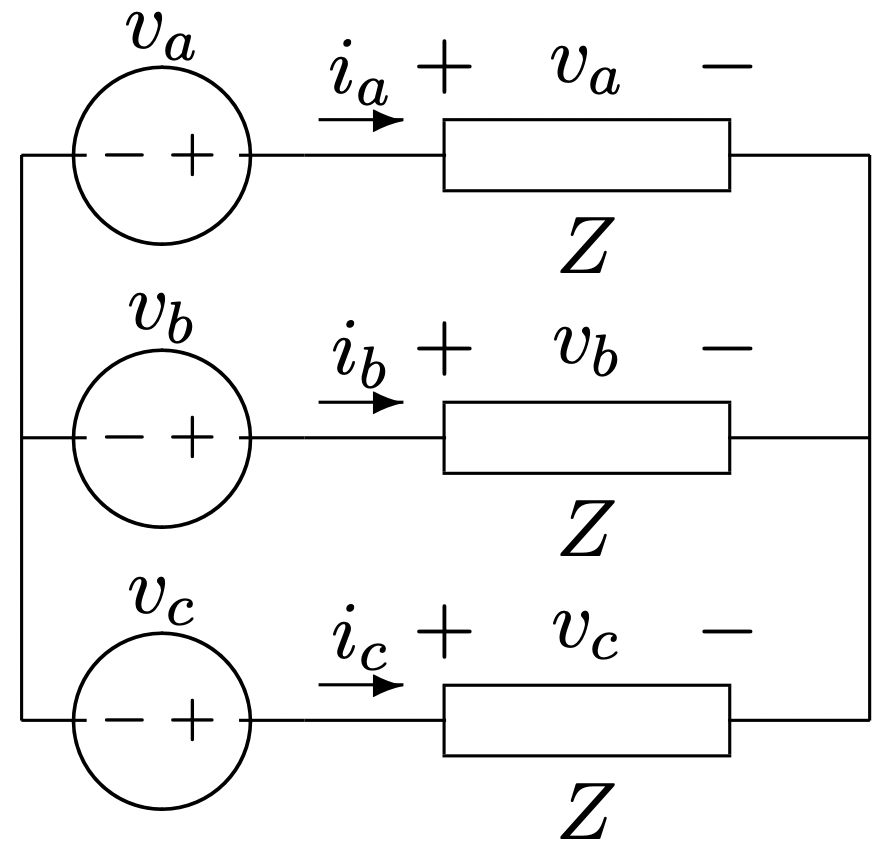Малюнок 7: Незаземлене трифазне джерело та навантаження

Існує принципова різниця між заземленими і незаземленими системами, якщо не підтримуються ідеально збалансовані умови. По суті, провід заземлення забезпечує ізоляцію між фазами шляхом фіксації нейтральної напруги в точці зірки рівним нулю. Якщо імпеданси навантаження не рівні, навантаження вважається незбалансованим. Якщо система заземлена, в нейтралі буде струм. Якщо незбалансована навантаження не заземлена, напруга зоряної точки не буде нульовим, а напруги будуть різними в трьох фазах при навантаженні, навіть якщо всі джерела напруги мають однакову величину.