Skip to main content
LibreTexts - Ukrayinska

3.1: Дві фази

  1. Last updated
  2. Save as PDF
  • Page ID
    32740

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Двофазна система є найпростішою з усіх поліфазних систем для опису. Розглянемо пару джерел напруги, що сидять поруч з:

    \[\ v_{1}=V \cos \omega t\label{1} \]

    \(\ v_{2}=V \sin \omega t\label{2}\)

    Припустимо, ця система джерел пов'язана з аль «збалансованим навантаженням», як показано на малюнку 1. Для обчислення потоків потужності в системі зручно перезаписувати напруги в складному вигляді:

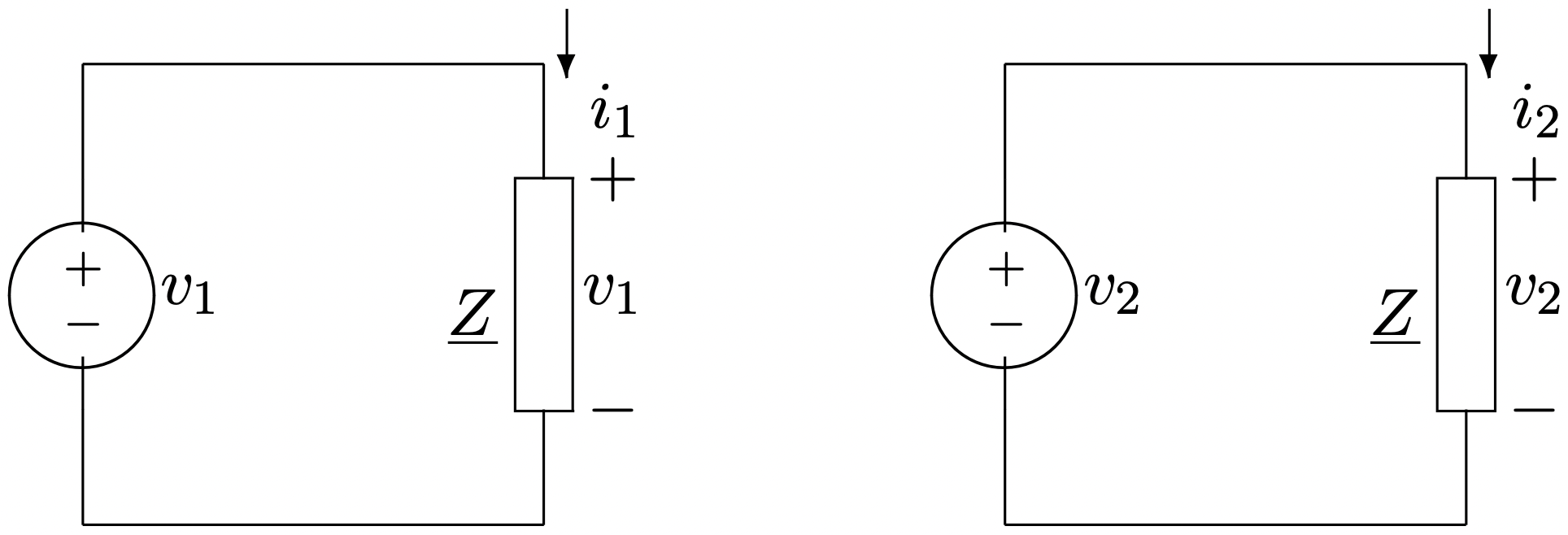    Знімок екрана 2021-07-20 о 12.40.55 PM.pngМалюнок 1: Двофазна система

    \(\ v_{1}=R e\left[\underline{V} e^{j \omega t}\right]\label{3}\)

    \(\ v_{2}=R e\left[-j \underline{V} e^{j \omega t}\right]\label{4}\)

    \(\ ={Re}\left[\underline{V} e^{j\left(\omega t-\frac{\pi}{2}\right)}\right]\label{5}\)

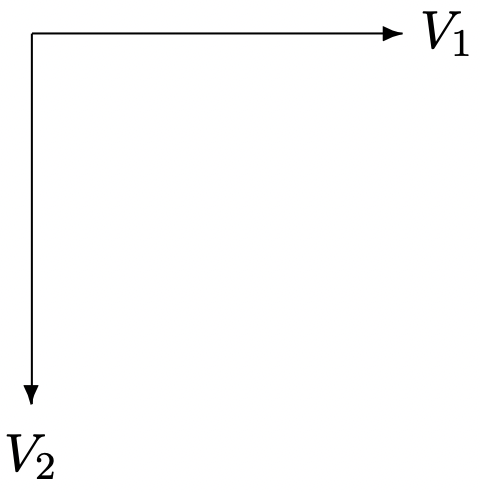    Знімок екрана 2021-07-20 о 12.43.32 PM.pngМалюнок 2: Фазорова діаграма для двофазного джерела

    Якщо кожне джерело підключено до навантаження з імпедансом:

    \(\ \underline{Z}=|\underline{Z}| e^{j \psi}\)

    тоді комплексні амплітуди струмів складають:

    \ (\\ begin {масив} {l}
    \ підкреслення {I} _ {1} =\ frac {\ підкреслення {V}} {|\ підкреслення {Z} |} e^ {-j\ psi}
    \ підкреслення {I} _ {2} =\ frac {\ підкреслення {V}} {|\ підкреслення {Z} |} e^ {-j\ psi} e^ {-j\ розрив {\ pi} {2}}
    \ end {масив}\)

    Кожна з двох фазних мереж має однакове значення для реальної і реактивної потужності:

    \(\ P+j Q=\frac{|\underline{V}|^{2}}{2|\underline{Z}|} e^{j \psi}\label{6}\)

    або:

    \(\ P=\frac{|\underline{V}|^{2}}{2|\underline{Z}|} \cos \psi\label{7}\)

    \(\ Q=\frac{|\underline{V}|^{2}}{2|\underline{Z}|} \sin \psi\label{8}\)

    Взаємозв'язок між «складною силою» і миттєвим потоком потужності була розроблена в главі 2 цих заміток. Для системи з напругою виду:

    \(\ v=R e\left[V e^{j \phi} e^{j \omega t}\right]\)

    миттєва потужність задається:

    \(\ p=P[1+\cos 2(\omega t+\phi)]+Q \sin 2(\omega t+\phi)\)

    Для розглянутої справи тут,\(\ \phi=0\) для фази 1 та\(\ \phi=-\frac{\pi}{2}\) для фази 2. Таким чином:

    \ (\\ begin {масив} {l}
    p_ {1} =\ frac {|\ підкреслення {V} |^ {2}} {2|\ підкреслення {Z} |}\ cos\ psi [1+\ cos 2\ омега т] +\ frac {|\ підкреслення {V} |^ {2}} {2|\ підкреслення {Z} |}\ sin\ psi\ sin 2\ омега т\\
    p_ {2} =\ frac {|\ підкреслення {V} |^ {2}} {2|\ підкреслення {Z} |}\ cos\ psi [1+\ cos (2\ омега т-\ пі)] +\ frac {|\ підкреслення {V} |^ { 2}} {2|\ підкреслення {Z} |}\ sin\ psi\ sin (2\ омега т-\ пі)
    \ кінець {масив}\)

    Зверніть увагу, що змінюються в часі частини цих двох виразів мають протилежні ознаки. У сукупності вони дають миттєву потужність:

    \(\ p=p_{1}+p_{2}=\frac{|\underline{V}|^{2}}{|\underline{Z}|} \cos \psi\)

    Принаймні одна з переваг поліфазних електромереж зараз очевидна. Використання збалансованої поліфазної системи дозволяє уникнути пульсацій потоку потужності через змінну напругу і струм, і навіть пульсацій через потік реактивної енергії. Це має очевидні переваги при роботі з двигунами та генераторами або, насправді, будь-яким типом джерела або навантаження, які хотіли б бачити постійну потужність.