5.9: Транспровідність

Last updated

Oct 25, 2022
Save as PDF
- 5.8: Температурна залежність струму в вимкненому стані
- 5.10: Балістичний квантовий провід FET

Marc Baldo
Massachusetts Institute of Technology via MIT OpenCourseWare

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Польовий транзистор - це джерело струму, кероване напругою. Його вхід - потенціал затвора, а на виході - струм джерела-стоку. У додатках ми зазвичай хочемо, щоб FET посилював невеликі зміни в $V_{GS}$ . Таким чином, важливою фігурою заслуг для транзистора є транспровідність, визначена як

$g_{m} = \frac{dI_{ds}}{dV_{gs}} \nonumber$

У вимкненому стані квантова ємність мала, і лише вплив воріт на транзисторний транзистор - це його електростатичний контроль потенціалу каналу. З Рівняння (5.3.1) ми бачимо, що цей контроль максимізується, коли

$C_{G} \gg C_{S},C_{D} \nonumber$

Це важлива мета проектування для транзисторів. Під цією межею транспровідність зазвичай виражається у вигляді:

$\frac{g_{m}}{I_{ds}} = \frac{1}{I_{ds}}\frac{dI_{ds}}{dV_{gs}} = \frac{q}{kT} \nonumber$

Хороший електростатичний контроль каналу може бути досягнутий або збільшенням діелектричної проникності ізолятора затвора, або зменшенням товщини ізолятора затвора.

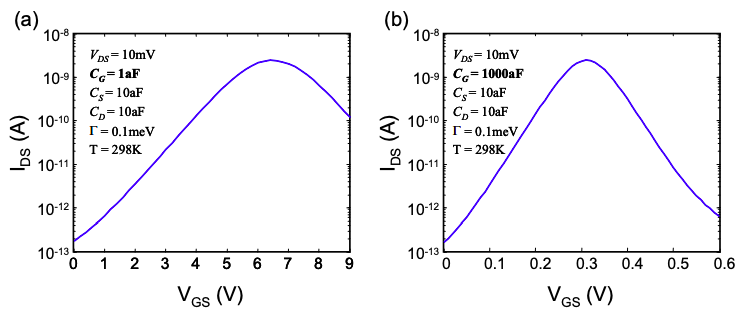
Хорошим емпіричним правилом є те, що затвор повинен знаходитися набагато ближче до каналу, ніж або контакти джерела, або зливу. Малюнок 5.9.1 показує вплив зміни $C_{G}$ на наш молекулярний транзистор C60. $C_{G}$ Збільшення зміщує напругу комутаційного затвора набагато нижче.

Цікаво, що для отримання цієї ідеальної характеристики ми $C_{G}$ збільшили на три порядки щодо більш практичного значення, використовуваного спочатку. Це відповідає збільшенню діелектричної проникності або зменшенню поділу затвор-канал на три порядки.

Знімок екрана 2021-05-18 о 18.50.png — Малюнок $\PageIndex{1}$ : Порівняння двох FET C60. В (а) затвор має поганий електростатичний контроль над каналом, про що свідчить малий $C_{G}$ . У (б) управління краще, а напруга комутації значно нижче.

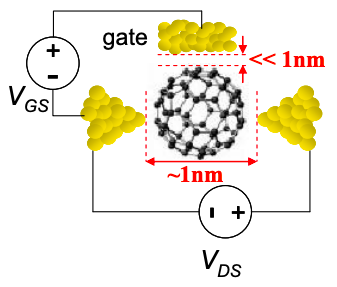
Для молекулярного транзистора з розділенням джерела-стоку на кілька нанометрів, ізолятор затвора повинен бути лише кілька Ångstroms — занадто тонкий, щоб достатньо ізолювати затвор. Це є можливо непереборною перешкодою для 0-d канальних пристроїв, таких як одиночні молекули FET.

Знімок екрана 2021-05-18 о 18,51,45, — Малюнок $\PageIndex{2}$ : Для високої транспровідності ємність затвора повинна бути набагато вище, ніж ємність вихідного або зливного каналу. Це змушує непрактично малі розділення затвор-каналу в молекулярних транзисторах.

1d і 2d транзистори

Центральне рівняння провідності

$I=\frac{q(N_{S}-N_{D})}{\tau} \nonumber$

У 0-d постійна часу $\tau$ , була визначена як сума часу міжфазного перенесення електронів $\tau_{S}$ і $\tau_{D}$ , яка, в свою чергу, може розглядатися як уявлення про енергію взаємодії між 0-d провідником і контактами джерела і стоку: $\tau_{S}=\Gamma_{S}/\hbar$ і $\tau_{D}=\Gamma_{D}/\hbar$ , відповідно.

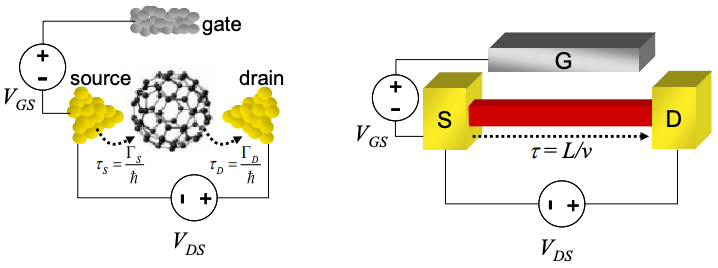
Знімок екрана 2021-05-18 о 18,57.02.png — Малюнок $\PageIndex{3}$ : (а) Час перенесення електронів в 0-d провіднику пов'язані з енергією взаємодії $\Gamma$ між контактом і провідником. (б) У вищих вимірах ми повинні визначити час проходження від швидкості електронів.

Однак у більш високих розмірах час перенесення електронів на контактах менш важливий. Швидше, $\tau$ це час транзиту електрона в провіднику. Це дається

$\tau=\frac{L_{x}}{v_{x}} \nonumber$

де $L_{x}$ - довжина каналу, і $v_{x}$ - швидкісна складова електрона паралельно струму джерело-стік. Важливо відзначити, що в 1-d, 2-d і 3-d провідниках час проходження залежить від енергії електрона, оскільки швидкість електронів $v_{x}$ , залежить від енергії.

Інша важлива зміна від 0-d моделі стосується щільності станів. У 0-d всі стани доступні електронам як з контактів джерела, так і стоку. Але в балістичних пристроях вищих розмірів електрони, що вводяться з джерела, здатні отримувати доступ лише до станів з моментами, спрямованими подалі від джерела. Ми називаємо ці стани +k. Аналогічно, стік лише впорскує електрони в —k стани. Таким чином, ми розбиваємо співвідношення дисперсії та щільність станів на дві частини, задана щільність станів +k $g^{+}(E)dE$ і задана щільність станів —k $g^{-}(E)dE$ .

Підводячи підсумок, в 1-d, 2-d і 3-d фундаментальні рівняння для транзистора такі:

$U_{ES} = -qV_{GS}\frac{C_{G}}{C_{ES}}-qV_{DS}\frac{C_{D}}{C_{ES}}+\frac{q^{2}}{C_{ES}}(N-N_{0}) \nonumber$

$N=N_{S}+N_{D} \nonumber$

$I=\frac{q}{\tau}(N_{S}-N_{D}) \nonumber$

де

$N_{S} = \int^{\infty}_{-\infty} g^{+}(E-U)f(E, \mu_{S})dE \nonumber$

$N_{D} = \int^{+\infty}_{-\infty} g^{-}(E-U)f(E, \mu_{D})dE \nonumber$