5.15: Проблеми

1. Фет з баскетболу

Парк та ін. повідомили про вимірювання Buckyball (C60) FET. Орієнтовна модель їх пристрою показана на малюнку 5.15.1. Виміряна провідність в залежності від$V_{DS}$ і$V_{GS}$ показана на рис.5.15.2.

Малюнок$\PageIndex{1}$: Геометрія C60 FET. Крім того, візьміть температуру T = 1K, а рівень молекулярної енергії розширення,$\Gamma = 0.1 eV$. LUMO знаходиться на рівні -4,7 еВ, а енергія Фермі в рівновазі$E_{F} = -5.0\ eV$

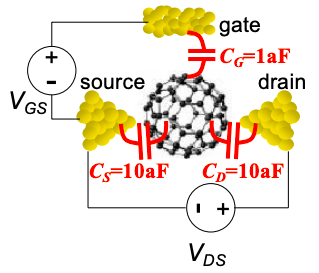
(а) Обчисліть провідність,$(dI_{DS}/dV_{DS})$ використовуючи параметри, наведені на малюнку 5.15.1. Розглянемо$5V<V_{GS}<8V$ розраховані з інтервалами 0,2 В і$-0.2V<V_{DS}<0.2V$ розраховані з інтервалами 10мВ.

(б) Поясніть Х-форму графіка провідності.

(c) Зауважте, що Парк та ін. виміряти ненульову провідність у верхньому і нижньому квадрантах. Намалюйте їх$I_{DS}-V_{DS}$ характеристику на$V_{GS} ~ 5.9V$. Порівняйте з Вашою розрахунковою$I_{DS}-V_{DS}$ характеристикою на$V_{GS} ~ 5.9V$. Запропонуйте пояснення ненульової провідності, виміряної в експерименті у верхньому і нижньому квадрантах.

Малюнок$\PageIndex{2}$:$(dI_{DS}/dV_{DS})$ Провідність C60 FET, виміряна Park et al. Ігноруйте три стрілки на сюжеті. З парку та ін. «Наномеханічні коливання в одному транзисторі С60» Nature 407 57 (2000). Надано видавничою групою «Природа». Використовується з дозволу.

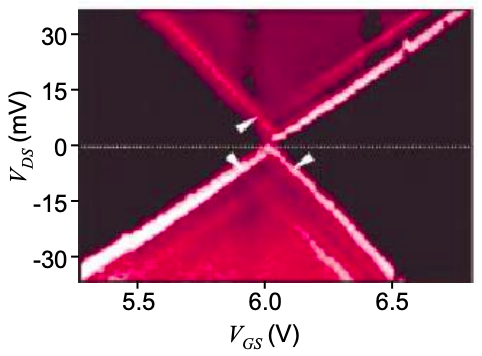
(d) У парку та ін. ' S вимірювання провідності зазор зникає при$V_{GS} = 6.0V$. Припускаючи, що$C_{G}$ це невірно на малюнку 5.15.1, обчисліть правильне значення.

Довідка

Парк та ін. «Наномеханічні коливання в одному транзисторі С60» Nature 407 57 (2000)

2. Дворежимний квантовий провід FET

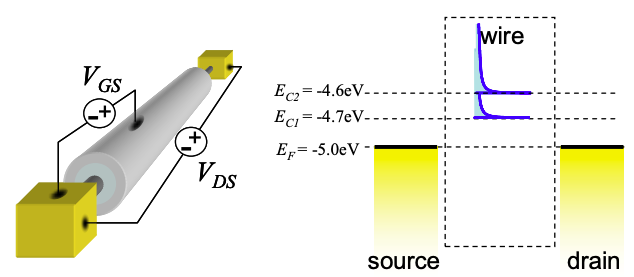
Розглянемо квантовий провід FET рис.5.17 в тексті.

Припустимо, що квантовий провід має два режими в$E_{C1} = -4.7eV$, і$E_{C2} = -4.6eV$. Аналітично визначити$I_{DS}-V_{DS}$ характеристики для варіювання$V_{GS}$ при Т = 0К. Намалюйте своє рішення для$0<V_{DS}<0.5$, при$V_{GS}$ = 0,3 В, 0,35 В, 0,4 В, 0,45 В і 0,5 В.

Виділіть різницю в IV характеристиках за рахунок додаткового режиму.

Малюнок$\PageIndex{3}$: Квантовий провід FET з двома режимами. Довжина дроту L = 100nm, ємність затвора -$C_{G} = 50\ aF$ на нанометр довжини дроту, а маса електронів, м, в дроті дорівнює$m=m_{0}=9.1\times 10^{-31} kg$. Припустимо$C_{S}$ і$C_{D} = 0$.

3. 2-d балістичний FET

(а) Чисельно обчислити вольт-амперні характеристики одномодового 2-d балістичного транзистора за допомогою рівняння (5.13.5) та самоузгодженого рішення для потенціалу, U. Побудуйте своє рішення для Т = 1К і Т = 298К. У кожному сюжеті розглянемо діапазон напруги$0<V_{DS}<0.5$, при$V_{GS}$ = 0,3 В, 0,35 В, 0,4 В, 0,45В і 0,5 В. У вашому розрахунку візьміть дно смуги провідності рівним -4,7 еВ, енергія Фермі при рівновазі$E_{F} = -5.0 eV$, L = 40nm, W = 3 × L, і$C_{G} = 0.1 fF$. Припустимо$C_{D} = C_{S} = 0$. Візьміть ефективну масу, м, як$m = 0.5 \times m_{0}$, де$m_{0} = 9.1\times10^{-31} kg$.

Слід отримати IV характеристики, наведені на малюнку 5.13.1.

(b) Далі порівняйте свої числові рішення з аналітичним розв'язком для лінійних областей та областей насичення (Рівняння (5.13.12) та (5.13.13)). Поясніть розбіжності.

(c) Чисельно визначити$I_{DS}$ vs$V_{GS}$ at$V_{DS}= 0.5V$ і T = 298K. Побудуйте струм за логарифмічною шкалою, щоб продемонструвати, що транспровідність становить 60 мВ/десятиліття в підпороговій області.

(d) Використовуючи свій графік у (c), виберіть новий$V_{T}$ такий, щоб аналітичне рішення для області насичення (Рівняння (5.13.13)) забезпечує кращу посадку при кімнатній температурі. Поясніть свій вибір.

4. Проводиться експеримент на канальному провіднику в трьох клемних пристроях. І джерело, і стік заземлені, при цьому потенціал затвора змінюється. Припустимо, що$C_{G} \gg C_{S},\ C_{D}$.

Малюнок$\PageIndex{4}$: Вимірювання поверхневого потенціалу транзисторного каналу.

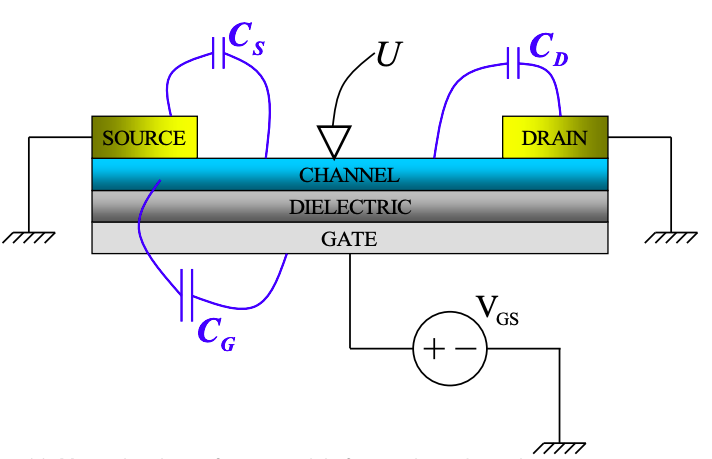
Транзистор зміщений вище порогу$(V_{GS} > V_{T})$. Вимірювання потенціалу каналу, U, показує лінійну варіацію зі збільшенням$V_{GS} > V_{T}$.

За яких умов може бути провідник:

(i) квантова точка (0 розміри)?

(ii) квантовий дріт (1 вимір)?

(iii) квантова яма (2 виміри)?

Поясніть свої відповіді.

5. Розглянемо три клеми молекулярного транзистора.

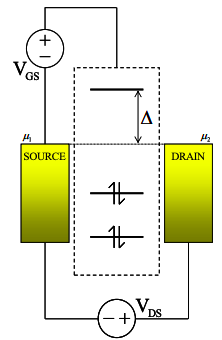
(а) Припустимо, що молекула містить лише одну незаповнену молекулярну орбіталь з енергією D вище рівноважного рівня Фермі. Припустимо і те, що$C_{G} \gg C_{S},\ C_{D}$ і$\Delta \gg kT$. Обчисліть транспровідність для малих$V_{DS}$ як функція T і$V_{GS}$ for$V_{GS} \ll \Delta$.

Висловіть свою відповідь з точки зору$I_{DS}$.

Малюнок$\PageIndex{5}$: Молекулярний транзистор з дискретними енергетичними рівнями в каналі.

(б) Тепер припустимо, що щільність молекулярних станів дорівнює

$$g(E) = \frac{1}{E_{T}} \text{exp}\left[ \frac{E-\Delta}{E_{T}} \right] u(\Delta - E) \nonumber$$

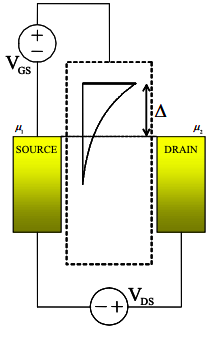
де$E_{T} \gg kT$. Обчисліть транспровідність для малих$V_{DS}$ як функція T і$V_{GS}$ for$V_{GS} \ll \Delta$. Припустимо$C_{G} \rightarrow \infty$.

Висловіть свою відповідь з точки зору$I_{DS}$.

Малюнок$\PageIndex{6}$: Молекулярний транзистор з експоненціальним DOS в каналі.

(c) Обговоріть наслідки вашого результату для молекулярних транзисторів.

6. Розглянемо звичайні n-канальні MOSFET, проілюстровані нижче:

Малюнок$\PageIndex{7}$: Структура звичайного МОП-транзистора.

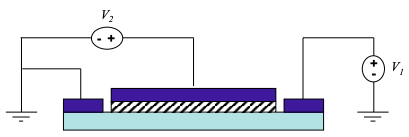
Припустимо$V_{T} = 1V$ і$V_{2} = 0V$. Намалюйте очікувані IV характеристики (I проти$V_{1}$) і поясніть, посилаючись на смугові діаграми, чому IV характеристики не симетричні.

7. Розглянемо балістичну квантову яму FET при T = 0K.

Малюнок$\PageIndex{8}$: Квантова свердловина FET нижче порогу.

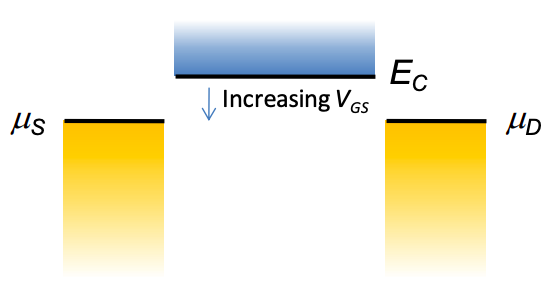
Нагадаємо, що загальним рішенням для квантової ями FET в насиченні є:

$$I_{DS} = \frac{qW}{\pi^{2}\hbar^{2}}\sqrt{\frac{8m}{9}} (\eta q (V_{GS-V_{T}}))^{3/2} \nonumber$$

(а) У межі$C_{Q} \gg C_{ES}$, що, нижня частина смуги провідності$E_{C}$, «приколота» до$\mu_{S}$ порогу. Покажіть, що за цих умов$\eta \rightarrow 0$.

(b) Чому провідність нульового каналу на порозі в цій межі?

(c) Враховуючи$C_{OX} = C_{G}/(WL)$, що, де W і L - ширина і довжина каналу, відповідно, показують, що струм насичення в цій балістичній квантовій ямі FET задається

$$I_{DS} = \frac{8 \hbar W}{3m\sqrt{\pi q}}\left( C_{OX} \left( V_{GS}-V_{T} \right) \right)^{3/2} \nonumber$$

Підказка: Висловіть квантову ємність в загальному розв'язку з точки зору параметрів пристрою m, W і L.

8. Квантова свердловина підключається до контактів джерела і зливу. Припустимо ідентичні контакти джерела і зливу.

Малюнок$\PageIndex{9}$: Квантова свердловина з вихідним і зливним контактами.

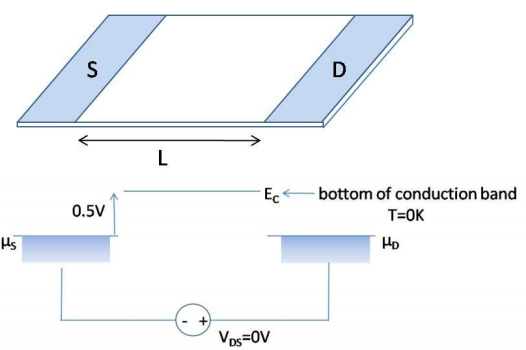
(а) Побудуйте потенційний профіль вздовж свердловини, коли$V_{DS} = +0.3V$.

Тепер над колодязем розташовують електрод затвора. Припустимо, що,$C_{G}\ggC_{S},\ C_{D}$ крім дуже близьких до джерела і зливних електродів. На$\epsilon = 4 \times 8.84 \times 10^{-12}\ F/m$ затворі електрода d = 10 нм. Припустимо, що контакти джерела і зливу ідентичні.

Малюнок$\PageIndex{10}$: Квантова яма з електродом затвора також.

(b) Що таке потенційний профіль, коли$V_{DS} = 0.3V$ і$V_{GS} = 0V$.

(c) Повторити (б) для$V_{DS} = 0V$ і$V_{GS} = 0.7V$. Підказка: Перевірте$C_{Q}$.

(d) Повторити (b) для$V_{DS} = 0.3V$ і$V_{GS} = 0.7V$ припустити балістичний транспорт.

(e) Повторити (b) для$V_{DS} = 0.3V$ і$V_{GS} = 0.7V$ припускаючи небалістичний транспорт.

9. Цю задачу розглядає 2-d квантова яма FET. Припустимо наступне:

Т = 0К, Л = 40 нм, Ш = 120 нм,$C_{G}$ = 0,1фф,$C_{S} = C_{D} = 0$

Малюнок$\PageIndex{11}$: 2-d квантова яма FET.

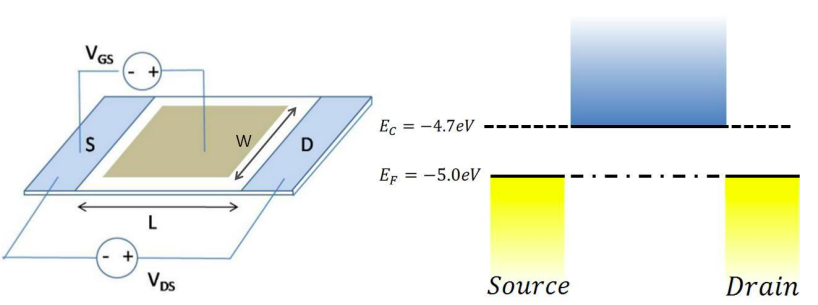
(а) Порівняти роботу 2-D свердловини в балістичному та напівкласичному режимах.

Припустимо$C_{Q} \rightarrow \infty \gg C_{ES}$ в обох режимах.

Приймати$\mu = 300\text{ cm}^{2}/Vs$ в напівкласичному режимі.

Сюжет$I_{DS}$ vs$V_{DS}$ для$V_{GS} = 0.5V$ і$V_{DS} = 0 \text{ to } 0.5V$.

(б) Поясніть різницю в кривих IV. Чи є проблема з теорією? Якщо так, то що?