Skip to main content
LibreTexts - Ukrayinska

1.25: Квадратний колодязь

  1. Last updated
  2. Save as PDF
  • Page ID
    31996

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Далі ми розглянемо одиночний електрон в межах квадратної потенційної ямки, як показано на малюнку 1.25.1. Як згадувалося в обговоренні фотоелектричного ефекту, електрони всередині твердих тіл пов'язані привабливими ядерними силами.

    Моделюючи енергію зв'язування всередині твердого тіла як квадратної свердловини, ми повністю ігноруємо тонкомасштабну структуру всередині твердого тіла. Звідси квадратний колодязь, або частка в коробці, як це часто відомо, є одним з найгрубіших наближень для електрона всередині твердого тіла. Простота наближення квадратної свердловини, однак, робить її однією з найкорисніших проблем у всій квантовій механіці.

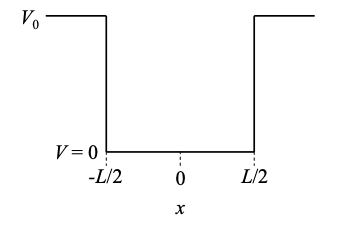
    Знімок екрана 2021-04-15 о 10.04.18
    Малюнок\(\PageIndex{1}\): Квадратний колодязь. Усередині твердого тіла потенціал визначається рівним нулю. У вільному просторі, поза твердим, відштовхуючий потенціал знаходиться\(V_{0}\).

    Оскільки потенціал різко змінюється, ми розглядаємо кожну область постійного потенціалу окремо. Згодом ми повинні підключити рішення в різних регіонах. Вирішення проблеми таким чином відоме як кускове рішення.

    Тепер рівняння Шредінгера - це твердження про збереження енергії

    \[ \text{total energy (E)} = \text{kinetic energy (KE)}+\text{Potential energy (V)} \nonumber \]

    У класичній механіці ніколи не можна мати негативну кінетичну енергію. Таким чином, класична механіка вимагає, щоб E > V. Це відоме як класично дозволений регіон.

    Але в нашому квантовому аналізі ми знайдемо рішення для E < V. Це відомо як класично заборонений режим.

    Класично дозволений регіон

    Перестановка рівняння (1.23.5) дає диференціальне рівняння другого порядку:

    \[ \frac{d^{2}\psi}{dx^{2}} = -\frac{2m(E-V)}{\hbar^{2}}\psi \nonumber \]

    У цій області, E > V, розчини мають вигляд

    \[ \psi(x)=Ae^{ikx}+Be^{-ikx} \nonumber \]

    або

    \[ \psi(x)=A\ sin(kx)+B\ cos(kx) \nonumber \]

    де

    \[ k =\sqrt{\frac{2m(E-V)}{\hbar^{2}}} \nonumber \]

    У класично дозволеній області ми маємо коливальні розв'язки.

    Класично заборонений регіон

    У цій області E < V, а розв'язки мають вигляд

    \[ \psi(x)=Ae^{\alpha x} +Be^{-\alpha x} \nonumber \]

    тобто вони або ростуть, або розпадаються експоненціальні, де

    \[ \alpha = \sqrt{\frac{2m(V-E)}{\hbar^{2}}} \nonumber \]