1.9: Лінійні комбінації хвиль

Далі розглянемо комбінації різних складних експоненціальних функцій. Наприклад, на малюнку 1.9.1 ми будуємо хвильову функцію, яка могла б описати електрон, рівноймовірний у положенні$x_{1}$ та положенні$x_{2}$. Представлення k -простору - це просто накладання двох складних експоненціальних функцій, відповідних$x_{1}$ і$x_{2}$. $^{†}$

$$\psi(x)=c_{1}\delta(x-x_{1})+c_{2}(x-x_{2}) \Leftrightarrow A(\omega) = c_{1}e^{-ikx_{1}}+c_{2}e^{-ikx_{2}} \nonumber$$

Малюнок$\PageIndex{1}$: k -космічна хвильова функція, що відповідає двом позиціям$x_{1}$ і$x_{2}$ є просто суперпозицією k -простору уявлень$\delta(x-x_{1})$ і$\delta(x-x_{2})$.

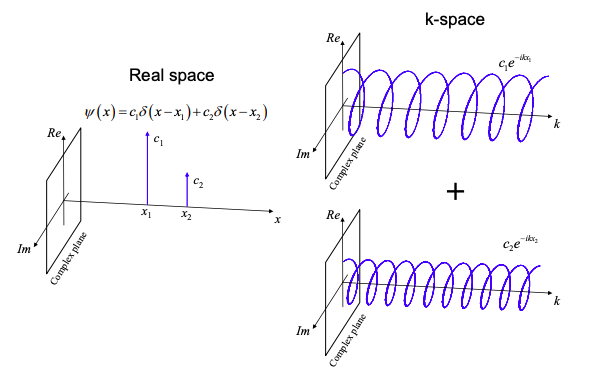
Ми також можемо узагальнити до довільного розподілу позицій,$\psi(x)$. Якщо$\psi(x)$ описує електрон, наприклад, ймовірність того, що електрон знаходиться в позиції х дорівнює$|\psi(x)|^{2}$. Таким чином, в k -просторі електрон описується сумою складних експоненціальних,$e^{-ikx}$ кожен коливається в k -просторі і зважений за амплітудою$\psi(x)$.

$$A(k)=\int^{+\infty}_{-\infty}\psi(x)e^{-ikx}dx \nonumber$$

Ви можете розпізнати це з 6.003 як перетворення Фур'є. Аналогічно, зворотне перетворення є

$$\psi(x)=\frac{1}{2\pi}\int^{+\infty}_{-\infty}A(k)e^{ikx}dk \nonumber$$

Для перетворення між часом і кутовою частотою використовуйте

$$A(\omega) =\int^{+\infty}_{-\infty} \psi(t)e^{i\omega t}dt \nonumber$$

і

$$\psi(t)=\frac{1}{2\pi}\int^{+\infty}_{-\infty} A(\omega)e^{-i\omega t}d\omega \nonumber$$

Зверніть увагу, що фактори$\frac{1}{2\pi}$ присутні кожного разу, коли ви інтегруєте стосовно k або$\omega$. Зауважте також, що при перетворенні між складними експоненціальними і дельта-функціями корисна наступна ідентичність:

$$2\pi\delta(u)=\int^{+\infty}_{-\infty} \text{exp}[iux]dx \nonumber$$

$^{†}$Зверніть увагу, що ця хвильова функція насправді не нормалізується.