5.5: Лінійний імпульс переглянуто

У цьому розділі розглядаються додаткові аспекти розрахунку лінійного імпульсу. Перший підрозділ розглядає використання відносних швидкостей, а другий підрозділ стосується використання циліндричних координат для опису криволінійного руху площини.

Використання відносних швидкостей

Наступний приклад ілюструє, як збереження лінійного імпульсу може бути використано для вирішення руху ракети, яка прискорюється. У цьому прикладі використовуються відносні швидкості.

Приклад - ракета, що прискорює

Невелика ракета, повністю завантажена паливом і окислювачем, має масу\(500 \ \mathrm{Mg}\), а\(80 \%\) із загальної маси складає паливо і окислювач. Ракета спрямована вертикально вгору і розміщена на стартовому майданчику на поверхні Землі. Після запалювання масова витрата вихлопної рідини з ракетного двигуна йде\(2300 \mathrm{~kg} / \mathrm{s}\) зі швидкістю виходу\(2100 \mathrm{~m} / \mathrm{s}\) відносно ракети. Нехтуючи силами тиску і опору рідини, визначити (а) скільки часу після займання відбувається перегорання (тобто ракета закінчується паливо і окислювач)? (б) як довго після займання відбувається зліт? і (в) яка швидкість руху ракети при прогоранні?

Рішення

Відомо: Маленька ракета злітає з поверхні землі.

Знайти: (а) час після запалювання до перегорання; (б) час після запалювання до вильоту; (c) швидкість ракети при прогоранні.

Дано:

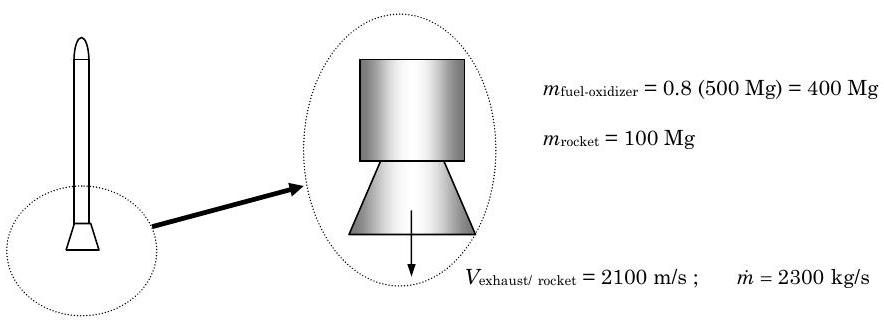
Малюнок\(\PageIndex{1}\): Дана інформація.

Аналіз:

Стратегія\(\rightarrow\) Оскільки ми стурбовані швидкістю прискорювального об'єкта і часом, необхідним для вичерпання маси палива і окислювача, давайте спробуємо використовувати масу і лінійний імпульс.
Система\(\rightarrow\) Візьміть відкриту, недеформуючу систему, яка включає в себе ракету з масою, що перетинає межу на вихлопі.
Властивість рахувати\(\rightarrow\) Як зазначено вище, спробуйте масу та лінійний імпульс.
Часовий інтервал\(\rightarrow\) Почніть з форми швидкості, а потім подивіться, що потрібно.

Малюнок\(\PageIndex{2}\): Вибір системи та напрямку масового потоку через межу.

Для системи вище маса витікає з дна ракети, як зазначено стрілкою. Щоб вирішити частину (а), напишіть збереження маси для системи; потім, інтегруючи з часом, ми маємо:\[\begin{align*} \frac{d m_{\text{sys}}}{dt} = -\dot{m}_{e} \quad & \rightarrow \quad \int\limits_{t_{1}}^{t_{2}} \left(\frac{d m_{\text{sys}}}{dt}\right) dt = \int\limits_{t_{1}}^{t_{2}} \left(-\dot{m}_{e}\right) dt \quad \rightarrow \quad m - m_{o} = -\dot{m}_{e} t \\ m = m_{o} - \dot{m}_{e} t \quad & \rightarrow \quad m=(500,000 \mathrm{~kg}) - \left( 2300 \ \frac{\mathrm{kg}}{\mathrm{s}}\right) t \end{align*} \nonumber \]

Зверніть увагу, що масова витрата розраховується щодо вихлопних газів ракети. При вигорянні маса системи дорівнює якраз масі порожньої ракети:\[t_{\text {burnout}} = \frac{(500,000 \mathrm{~kg} - 100,000 \mathrm{~kg})}{\left(2300 \ \dfrac{\mathrm{kg}}{\mathrm{s}}\right)} = 173.9 \text { seconds } \nonumber \]

Тепер, щоб вирішити час підйому, нам потрібно застосувати збереження лінійного імпульсу:\[ \begin{align*} \boxed{ \uparrow + } \quad\quad\quad\quad\quad\quad\quad\quad \frac{d P_{y, \ \text{sys}}}{dt} &= -mg - \dot{m}_e V_{y, \ e} \\[4pt] \frac{d \left( m V_G \right)}{dt} &= -mg - \dot{m}_e \underbrace{ \left( V_G - V_{\text{exhaust / rocket}} \right) }_{\begin{array}{c} \text{Absolute velocity of the exhaust} \\ \text{with respect to the ground} \end{array}} \\ m \frac{d V_G}{dt} + V_G \underbrace{ \cancel{ \frac{dm}{dt} }^{= - \dot{m}_e} }_{\begin{array}{c} \text{Using conservation} \\ \text{of mass results} \end{array}} &= -mg - \dot{m}_e \left( V_G - V_{\text{exhaust / rocket}} \right) \\ m \frac{d V_G}{dt} + V_G \left( - \dot{m}_e \right) &= -mg - \dot{m}_e \left( V_G - V_{\text{exhaust / rocket}} \right) \\ m \frac{d V_G}{dt} &= -mg - \dot{m}_e \left( V_G - V_{\text{exhaust / rocket}} \right) + \dot{m}_e V_G \\[4pt] m \frac{d V_G}{dt} &= -mg - \cancel{ \dot{m}_e V_G } + \dot{m}_e V_{\text{exhaust / rocket}} + \cancel{ \dot{m}_e V_G } \\[8pt] m \frac{d V_G}{dt} &= -mg + \dot{m}_e V_{\text{exhaust / rocket}} \end{align*} \nonumber \]

Уважно вивчіть кроки вище. Зверніть увагу, що ви повинні бути обережними, щоб використовувати абсолютну швидкість вихлопу, що виходить з вихлопу. Також зауважте, що ми використовуємо збереження рівняння маси для спрощення збереження лінійного імпульсу.

Щоб вирішити для частини (b) час відриву, ми можемо використовувати рівняння вище. При підйомі прискорення системи дорівнює нулю, так як тяга якраз врівноважує вагу сили тяжіння:\[m \cancel{ \frac{d V_G}{d t} }^{=0} = -mg + \dot{m}_{e} V_{\text {exhaust / rocket }} \quad \rightarrow \quad \begin{gathered} mg = \dot{m}_{e} V_{\text {exhaust / rocket}} \\ \left(m_{o}-\dot{m}_{e} t \right) g = \dot{m}_{e} V_{\text {exhaust / rocket}} \\ m_{o} g = \dot{m}_{e} \left(gt + V_{\text {exhaust / rocket}}\right) \end{gathered} \quad \rightarrow \quad t_{\text {liftoff}} = \frac{m_{o}}{\dot{m}_{e}} - \frac{V_{\text {exhaust / rocket}}}{g} \nonumber \]

Потім рішення за час зльоту:\[t_{\text {liftoff}} = \frac{m_{o}}{\dot{m}_{e}} - \frac{V_{\text {exhaust / rocket}}}{g} = \left(\frac{500,000 \mathrm{~kg}}{2300 \mathrm{~kg} / \mathrm{s}}\right) - \left(\frac{2100 \mathrm{~m} / \mathrm{s}}{9.81 \mathrm{~m} / \mathrm{s}^{2}} \right) = 3.32 \mathrm{~seconds} \nonumber \]

Нарешті, щоб вирішити швидкість при вигоранні, ми повинні обчислити швидкість ракети як функцію часу. Ми робимо це шляхом інтеграції рівняння прискорення для ракети. Спочатку переставляючи збереження лінійного імпульсу результату, маємо вираз для прискорення ракети:\[\frac{d V_{G}}{d t} = -g + \frac{\dot{m}_{e}}{m} V_{\text {exhaust / rocket }} \nonumber \]

Інтеграція цього з часом з точки зльоту дає наступне:\[ \begin{align*} \int\limits_{t_{\text{liftoff}}}^{t} \left( \frac{d V_G}{dt} \right) dt &= \int\limits_{t_{\text{liftoff}}}^{t} \left[ -g + \frac{\dot{m}_e V_{\text{exhaust / rocket}}}{\left( m_o - \dot{m}_e t \right)} \right] dt \\[4pt] \left. V_G - V_G \right|_{t_{\text{liftoff}}} &= \int\limits_{t_{\text{liftoff}}}^{t} \left[ -g \right] dt + \int\limits_{t_{\text{liftoff}}}^{t} \left[ \frac{\dot{m}_e V_{\text{exhaust / rocket}}}{\left( m_o - \dot{m}_e t \right)} \right] dt \\[4pt] V_G - \cancel{ \left. V_G \right|_{t_{\text{liftoff}}} }^{=0} &= -g \left( t - t_{\text{liftoff}} \right) + \dot{m}_e V_{\text{exhaust / rocket}} \left[ \frac{1}{\dot{m}_e} \int\limits_{t_{\text{liftoff}}}^{t} \frac{\dot{m}_e \ dt}{\left( m_o - \dot{m}_e t \right) } \right] \\[4pt] V_G &= -g \left( t - t_{\text{liftoff}} \right) + \dot{m}_e V_{\text{exhaust / rocket}} \left[ - \frac{1}{\dot{m}_e} \ \ln \left( \frac{m_o - \dot{m}_e t}{m_o - \dot{m}_e t_{\text{liftoff}}} \right) \right] \\[10pt] V_G &= -g \left( t - t_{\text{liftoff}} \right) - V_{\text{exhaust / rocket}} \left[ \ln \left( \frac{m_o - \dot{m}_e t}{m_o - \dot{m}_e t_{\text{liftoff}}} \right) \right] \end{align*} \nonumber \]

Зауважте, що це рівняння дійсне лише для\(t_{\text {liftoff}} \leq t \leq t_{\text {burnout}}\). Рішення для швидкості при вигоранні дає\[\begin{aligned} V_{G} &= -g \left(t_{\text {burnout}} - t_{\text {liftoff}}\right) - V_{\text {exhaust / rocket}} \left[\ln \left(\frac{m_{o}-\dot{m}_{e} t_{\text {burnout}}}{m_{o}-\dot{m}_{e} t_{\text {liftoff}}}\right)\right] \\[4pt] &= -\left(9.81 \ \frac{\mathrm{kg}}{\mathrm{s}}\right)(173.9-3.32) \mathrm{s}-\left(2100 \ \frac{\mathrm{m}}{\mathrm{s}}\right) \left[\ln \frac{(100 \ \mathrm{Mg})}{\left(500 \ \mathrm{Mg}-2.3 \ \dfrac{\mathrm{Mg}}{\mathrm{s}}(3.32 \mathrm{~s})\right)}\right] \\[4pt] &=\left(-1673 \ \frac{\mathrm{m}}{\mathrm{s}}\right) - \left(-3348 \ \frac{\mathrm{m}}{\mathrm{s}}\right) \\[4pt] &= 1675 \mathrm{~m} / \mathrm{s} \end{aligned} \nonumber \]

Коментарі

Наскільки над землею ракета опинилася б при вигоранні? Як ви могли це обчислити? Як ви вважаєте, наша модель точна аж до вигорання? Які можливі проблеми ви б побачили?

Якщо діаметр вихлопу сопла ракети є\(5 \mathrm{~m}\) і тиск вихлопних газів є\(10 \ \mathrm{kPa}\), визначте чисту силу тиску на систему. Припустимо, атмосферний тиск є\(100 \ \mathrm{kPa}\). Чи було нехтування силою тиску розумним?

Рух з циліндричними координатами

Наступна програма показує, як циліндричні координати можуть бути використані для опису плоского криволінійного руху.

Застосування - Плоский криволінійний рух в циліндричних координатах

Іноді вигідно описувати рух точки в площині через відстань\(r\) від початку і кута,\(\theta\) виміряного від позитивної\(x\) -осі, тобто циліндричних координат. Використовуючи визначення швидкості та прискорення як першої та другої похідних положення щодо часу та тригонометричних відносин між ними\(x, y, r,\), можуть бути розроблені наступні співвідношення:\(\theta\)

Рисунок\(\PageIndex{3}\): Таблиця одиничного вектора та положення, швидкості та рівняння прискорення між прямокутними та циліндричними координатами.

(a) Починаючи з вектора позиції\(\mathbf{r}\), покажіть, що\(\mathbf{e}_{\mathrm{r}}=(\cos \theta) \mathbf{i}+(\sin \theta) \mathbf{j}\).

(б) Тепер\(\mathbf{e}_{\mathbf{r}}\) диференціюйте по відношенню до часу і доведіть собі це\(\dfrac{d}{d t} \mathbf{e}_{\mathbf{r}}=\omega \mathbf{e}_{\theta}\).

(c) Як відносини для\(\mathbf{r}, \mathbf{V}\) і\(\mathbf{a}\) в циліндричних координатах спрощують\(r=R\), якщо, константу?

(d) Як відносини для і\(\mathbf{a}\) в циліндричних координатах спрощують\(\mathbf{r}, \mathbf{V}\), якщо\(\omega=\) постійні?

Приклад — Лінійний імпульс кругового диска

Круглий диск радіусу\(R\) і товщини\(t\) виготовляється з матеріалу з щільністю\(\rho\). Визначають лінійний імпульс для диска при наступних умовах:

(а) Диск обертається зі швидкістю обертання\(\omega\) навколо своєї центроїдальної осі,\(G\). Незважаючи на те, що цей диск, здається, торкається землі, він ковзає і не котиться.

(б) Диск ковзає вправо, не обертаючись, т\(\omega=0\). Диск перекладається зі швидкістю\(\mathbf{V}\).

Малюнок\(\PageIndex{4}\): Дана інформація про диск.

Рішення:

Відомо: круговий диск рухається із заданим рухом.

Знайти: (а) Лінійний імпульс, коли диск обертається навколо своєї центроїдальної осі.
(b) Лінійний імпульс, коли диск перекладається зі швидкістю\(\mathbf{V}\).

Дано: Див. Малюнок вище.

Аналіз: Стратегія\(\rightarrow\) Використовуйте визначення лінійного імпульсу.

(а) Швидкість обертового диска, виміряна щодо центру маси,\(G\) становить\(\mathbf{V} = r \omega \mathbf{e}_{\theta} = r \omega \left( -(\sin \theta) \mathbf{i}+(\cos \theta) \mathbf{j} \right)\). Використовуючи визначення лінійного імпульсу системи, ми маємо\[\begin{aligned} \mathbf{P}_{\mathrm{sys}} &= \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} (\mathbf{V} \rho) d V\kern-1.0em\raise0.3ex- = \int\limits_{0}^{2 \pi} \int\limits_{0}^{R} \underbrace{ \left(r \omega \mathbf{e}_{\theta} \right) }_{\mathbf{V}} \rho \underbrace{ (r \ d \theta \ dr) }_{d V\kern-0.5em\raise0.3ex-} \\ &= (\rho \omega) \int\limits_{0}^{2 \pi} \underbrace{ ((\sin \theta) \mathbf{i} - (\cos \theta) \mathbf{j}) }_{\mathbf{e}_{\theta}} \left( \int\limits_{0}^{R} r^{2} \ dr \right) d \theta = (\rho \omega) \int\limits_{0}^{2 \pi} \underbrace{ ((\sin \theta) \mathbf{i} - (\cos \theta) \mathbf{j}) }_{\mathbf{e}_{\theta}} \left( \frac{R^{3}}{3}\right) d \theta \\ &= \left( \frac{\rho \omega R^{3}}{3} \right) \int\limits_{0}^{2 \pi} \left( (\sin \theta) \mathbf{i} - (\cos \theta) \mathbf{j} \right) \ d \theta \\ &=\left( \frac{\rho \omega R^{3}}{3} \right) \left[ \mathbf{i} \int\limits_{0}^{2 \pi}(\sin \theta) \ d \theta - \mathbf{j} \int_{0}^{2 \pi}(\cos \theta) \ d \theta \right] = \left( \frac{\rho \omega R^{3}}{3} \right)(0)=0 \end{aligned} \nonumber \]

Таким чином, як ви вже здогадалися, лінійний імпульс диска, що обертається навколо своєї центроїдальної осі, однаково дорівнює нулю. Загалом, лінійний імпульс системи, що обертається навколо нерухомої осі, завжди дорівнює нулю, якщо (1) вісь обертання проходить через центр маси, тобто її центроїдальну вісь, і (2) система має площину симетрії, яка перпендикулярна осі обертання. Якщо будь-яке з цих двох умов порушено, лінійний імпульс не буде дорівнює нулю.

Зауважте, що цю інтеграцію можна було б значно спростити, якби ми використовували інтеграл для швидкості центру маси, Eq. \((5.1.16)\). Центр маси\(G\) диска знаходиться на осі обертання, а вісь обертання не перекладається; таким чином,\[\mathbf{P}_{\mathrm{sys}} = \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}}(\mathbf{V} \rho) d V\kern-1.0em\raise0.3ex- = m_{s y s} \cancel{ V_{G} }^{=0} =0 \nonumber \] і лінійний імпульс системи дорівнює нулю. Це набагато простіше, ніж робити повну інтеграцію!

(б) Починаючи з визначення лінійного імпульсу і того, що диск перекладається зі швидкістю\(\mathbf{V}\), ми маємо\[\begin{aligned} \mathbf{P}_{\mathrm{sys}} &= \int\limits_{V\kern-0.5em\raise0.3ex-_{\text {sys}}}(\mathbf{V} \rho) d V\kern-1.0em\raise0.3ex- = \int\limits_{0}^{2 \pi} \int\limits_{0}^{R}(\mathbf{V} \rho) \underbrace{ (rt \ d \theta \ d r)}_{d V\kern-0.5em\raise0.3ex-} = (\mathbf{V} \rho t) \int\limits_{0}^{2 \pi} \int\limits_{0}^{R} r \ dr \ d \theta \\ &=(\mathbf{V} \rho t) \int\limits_{0}^{2 \pi} \left(\int\limits_{0}^{R} r \ dr \right) d \theta = (\mathbf{V} \rho t) \int\limits_{0}^{2 \pi} \left(\frac{R^{2}}{2}\right) d \theta \\ &= (\mathbf{V} \rho t) \left( \frac{R^{2}}{2}\right) \int\limits_{0}^{2 \pi} d \theta =(\mathbf{V} \rho t) \left(\frac{R^{2}}{2}\right)(2 \pi) \\ &= \underbrace{ \left( \rho \left(\pi R^{2} t\right)\right) }_{\rho V\kern-0.5em\raise0.3ex- _{\text{sys}}} \mathbf{V} = m_{sys} \mathbf{V} \end{aligned} \nonumber \]

Таким чином, лінійний імпульс - це всього лише твір швидкості поступального руху та маси системи. Знову ж таки, цей розрахунок можна значно спростити, використовуючи рівняння швидкості центру мас:\[\mathbf{P}_{\mathrm{sys}}=\int_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} (\mathbf{V} \rho) d V\kern-1.0em\raise0.3ex- = m_{s y s} \cancel{ \mathbf{V}_{G} }^{=\mathrm{V}} = m_{sys} \mathbf{V} \nonumber \]