5.1: Чотири питання
Другий закон Ньютона, який зазвичай пишеться якF=ma, є одним з найвідоміших відносин у фізиці. Це співвідношення, поряд з першим і третім законами Ньютона, як правило, є відправною точкою для навчання механіки в середній школі та фізиці бакалавра. Інструкція механіки часто розбивається на три різні області: сили в стаціонарних системах, рух частинки, що піддається силі, і проблеми удару. Орієнтуючись на кожну область окремо, можна почати розвивати фізичне розуміння важливих фізичних явищ.
Коли інженери застосовують ці принципи до реалістичних проблем, вони вважають корисним мати більш загальну структуру, таку, яка забезпечує загальну основу для розробки корисних математичних моделей. Щоб забезпечити цю основу, ми розробляємо фізичний закон під назвою Збереження лінійного імпульсу, який, з невеликими обмеженнями, є універсально застосовним. Потім, як ми робили з масою та зарядом, ми вивчимо модельні припущення, які інженери зазвичай використовують при побудові математичних моделей фізичних систем.
При розробці концепції бухгалтерського обліку нового майна виникає чотири питання, на які необхідно відповісти. При застосуванні до лінійного імпульсу питання стають
- Що таке лінійний імпульс?
- Як лінійний імпульс може зберігатися в системі?
- Як можна транспортувати лінійний імпульс?
- Як можна створити або знищити лінійний імпульс?
Після того, як ми відповімо на ці питання, ми отримаємо відповідне бухгалтерське рівняння для лінійного імпульсу системи.
Що таке лінійний імпульс?
В якості відправної точки розглянемо рух дуже спеціалізованої системи, частинки. Частинка - це замкнута система, яка поводиться так, ніби її обсяг був незначним, а маса зосереджена в одній точці. Рух частинки повністю описується її швидкістю, і всі взаємодії між частинкою і її оточенням відбуваються в одній точці. Пізніше ми розглянемо більш реалістичні та більші розширені системи, для яких припущення про частинки недостатньо; однак ми виявимо, що припущення про частинки часто є дуже хорошою моделлю.
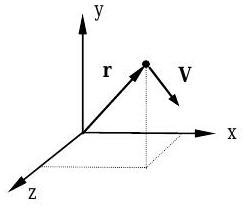
Малюнок5.1.1: Частинка з масоюm в положенніr зі швидкістюV.
Для частинки з масоюm і швидкістю5.1.1,V як показано на малюнку, лінійний імпульс частинкиP, визначається як добуток маси частинок і швидкості частинок:P=mV Розміри лінійного імпульсу з точки зору первинних розмірів є добуток розмірів маси і швидкості,[M][L]/[T]. Типові одиниці лінійного імпульсу знаходятьсяkg⋅m/s в СІ іslug⋅ft/s (абоlbm⋅ft/s) в УСК.
Важливо відзначити, що лінійний імпульсP, як і швидкістьV, є вектором. Як показано на малюнку5.1.2, вектори зазвичай представлені стрілками. Вектор - це математичний вираз, який має величину, напрямок і додає відповідно до закону паралелограма. Величина вектора описує «довжину» стрілки, і якщо вона представляє фізичну величину, то величина включає як число, так і пов'язані з ним одиниці. Напрямок вектора задається з точки зору його лінії дії та його сенсу. Як показано на малюнку5.1.2 векториPA іPB мають однакову величину і таку ж лінію дії, але протилежний сенс. Величина вектора є додатним числом і зображується математично якPA=|PA|. Повний вектор описується, задаючи величину і напрямок кожного вектора:PA=PA ∠θ=(5 kg⋅m/s) ∠θ іPB=PB ∠(θ+π)=(5 kg⋅m/s) ∠(θ+π), де всі кути вимірюються від опорної лінії.
.jpg)
Малюнок5.1.2: Величина і напрямок вектора.
Окрім величини та напрямку, вектори, що представляють лінійний імпульс та його транспорт, також мають точку застосування. Вектор з точкою застосування називається зв'язаним вектором. Підсумовуючи, лінійний вектор імпульсу повністю вказаний на] ce ми знаємо його величину, напрямок та точку застосування.
Оскільки лінійний імпульс частинки залежить від її маси, лінійний імпульс є великою властивістю. Як і при інших великих властивостях лінійний імпульс має інтенсивну форму. Лінійний імпульс на одиницю маси, або питомий лінійний імпульсp, визначається якp≡limV−sys→0Psysmsys=V Таким чином, швидкість частинки насправді є лише питомим лінійним імпульсом частинки.
Важливо зазначити, що швидкість, як і положення, завжди вимірюється відносно контрольної точки. При використанні для визначення лінійного імпульсу швидкість повинна бути виміряна відносно інерційної системи відліку. Для наших цілей це означає систему координат, яка не обертається і не прискорюється по відношенню до Землі, тобто закріплену Землею систему координат. Крім того, будь-яка система координат, яка рухається з постійною швидкістю по відношенню до Землі, також є інерційною системою відліку.
Як ми покажемо пізніше, часто корисно приєднати систему координат до рухомої системи, якщо система рухається з постійною швидкістю. За цих умов обчислюються всі швидкості щодо рухомої системи координат. Для руху космічного корабля вам потрібно буде використовувати сонцецентричну, не обертається опорну рамку. Дивіться будь-який підручник з фізики для студентів, щоб дізнатися більше про умови інерційної системи відліку.
5.1.1 Кінематика частинки
Через зв'язок швидкості до лінійного імпульсу розуміння кінематики відіграватиме вирішальну роль у нашому вивченні лінійного імпульсу. Кінематика - це вивчення геометрії руху без урахування причини руху і забезпечує взаємозв'язок між положеннямrV, швидкістю таa прискоренням точки. Вектор швидкостіV пов'язаний з вектором положенняr через основну кінематичну залежність, яку ви вивчили у фізиці - швидкість є першою похідною від положення:
V=drdtРозміри швидкості - довжина в одиницю часу,[L]/[T]. Типові одиниці для швидкості знаходятьсяm/s в СІ абоft/s в УСК.
Перша похідна швидкості (або друга похідна від положення) - вектор прискоренняa: Розміриa=dVdt=ddt(drdt) прискорення - довжина за одиницю часу в квадраті,[L]/[T]2. Типові одиниці для прискорення знаходятьсяm/s2 в СІ абоft/s2 в USCS.
Прямолінійний рух
При прямолінійному русі частинка може рухатися тільки по прямій лінії. За цих умов для опису положення частинок потрібна лише одна просторова координатаx, скажімо, а швидкість та прискорення записуються якV=dxdt and a=dVdt=d2xdt2 Ці відносини є найбільш кориснимиx, коли положенняV, швидкість та прискоренняa є функціями час. В умовах прямолінійного руху позитивне числове значення швидкості передбачає, що частинка рухається в тому ж напрямку, що і позитивнаx -вісь. Аналогічно, додатне числове значення для прискорення передбачає, що швидкість частинки збільшується в міру її руху в напрямку позитивноїx -осі.
Альтернативний вираз для прискорення іноді корисний, якщо прискорення і швидкість відомі як функції положення, наприкладV=V(x) іa=a(x). У цих умовах прискорення можна записати як=fx(t)V=fV(x)→a≡dVdt=Chain Rule of Differentiation⏞(dVdx)(dxdt)⏟=V=VdVdxa=fa(x) використання ланцюгового правила диференціації від числення. Зауважте, що позначенняf(t) "" читається як «функціяt.»
Однією із загальних завдань кінематики є інтеграція прискорення (часової швидкості зміни або першої похідної швидкості) точки щодо часу або щодо положення. Не запам'ятовуйте формули, описані нижче. Кожен з результатів відрізняється, але підхід однаковий. Вивчіть процес, а не результат!
Випадок I: Прискорення відоме як функція часу, наприкладa=f(t). Щоб знайти швидкість, інтегруйте по відношенню до часу наступним чином:a=f(t)=dVdt→dV=f(t)dt→V−Vo=t∫tof(t) dt
Практика: (а) Враховуючи, щоa=bt іV=Vo вt=0 s, розробити рівняння швидкостіV. (б) Визначити швидкість приt=5 s, якщоb=15 m/s3 іVo=20 m/s.
Випадок II: Прискорення відоме як функція положення, наприкладa=f(x). Швидкість може бути визначена шляхом інтеграції щодо положення, як показано нижче:a=f(x)=VdVdx→V dV=f(x)dx→V22−V2o2=x∫xof(x) dx
Практика: (а) Враховуючи, щоa=cx іV=Vo вx=0, розробити рівняння швидкостіV. (б) Визначити швидкість приx=5 m, якщоc=10 s−2 іVo=10 m/s.
Випадок III: Прискорення відоме як функція швидкості, наприкладa=f(V). Швидкість може бути визначена шляхом інтеграції щодо часу або положення, як показано нижче:a=f(V)=dVdt→dt=dVf(V)→t−to=V∫VodVf(V)a=f(V)=VdVdx→dx=[Vf(V)]dV→x−xo=∫VVo[Vf(V)] dV
Практика: (а) Враховуючи, щоa=bV2 іV=Vo вx=xo, розробити рівняння швидкостіV. (б) Враховуючи, щоa=bV2 іV=V0 вt=to, розробити рівняння швидкостіV.
Випадок IV: Прискорення є константою, наприкладa=constant. Швидкість може бути визначена шляхом інтеграції щодо часу або положення, як показано нижче:a= constant →a=dVdt→dV=a dt→V−Vo=a(t−to)a=VdVdx→V dV=a dx→V22−V2o2=a(x−xo)
Практика: Починаючи з визначення швидкостіV=dx/dt, доведіть, що положення можна описати рівнянням видуx−xo=Vot+(1/2)at2.
Площина криволінійного руху
При плоскому (або двовимірному) криволінійному русі рух обмежується площиною. Запис вектора положенняr (рисунок5.1.3) для точки на площині через її прямокутні складові дає,r=xi+yj деi іj є два ортогональних одиничних вектора іx іy є відповідними відстанями, виміряними у напрямку кожного одиниця вектора.
.png)
Малюнок5.1.3: Прямокутні координа
Диференціювання Eq. 5.1.7як того вимагає Eq. 5.1.3дає вектор швидкості в терміні його складових
V=ddt(xi+yj)=d(xi)dt+d(yj)dt=(dxdti+xdidt=0)+(dydtj+ydjdt=0)=(dxdt)i+(dydt)j=Vxi+Vyj
деVx іVy є складовими швидкості вx іy напрямках відповідно. Згадайте з вашого дослідження числення, що похідна константи, наприклад, одиничний векторi, однаково дорівнює нулю. Аналогічно можна показати, що вектор прискорення має складові:a=dVdt=ddt(Vxi+Vyj)=dVxdti+dVydtj=axi+ayj деax іay є складові швидкості вx іy напрямках відповідно.
Відносний рух
Нагадаємо, що при обчисленні лінійного імпульсу системи всі швидкості повинні бути виміряні щодо інерційного, тобто неприскорювального, еталонного кадру. Таким чином, якщо швидкість вимірюється в прискорювальному опорному кадрі, потрібно буде визначити абсолютну швидкість, перш ніж ми зможемо обчислити лінійний імпульс системи. Крім того, якщо система перекладається з постійною швидкістю, вона іноді спрощує задачу обчислення лінійного імпульсу щодо цього рухомого, інерційного опорного кадру.
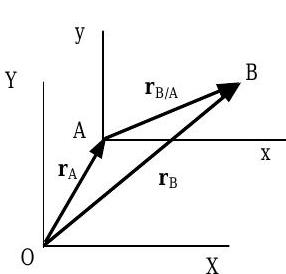
Малюнок5.1.4: Відносне положення.
ВекторrB/A відносного положення точки по відношенню до точкиA (див.B Рис.5.1.4) визначається співвідношенням:rB/A=rB−rA
де вектор положенняrA точкиA і вектор положенняrB точки обидваB вимірюються відносно точкиO, початок системи координат XYZ. Задано відносне положення точкиB по відношенню до точкиA і абсолютне положення точкиA, Eq. 5.1.10можна переписати, як показано нижче, щоб знайти абсолютну швидкість точкиB:rB=rA+rB/A
Подібні відносини можна записати для відносної і абсолютної швидкостей точокA іB:VB/A=VB−VA→VB=VA+VB/AaB/A=aB−aA→aB=aA+aB/A
Уявіть собі, що залізничний вагон прискорюється і рухається вправо з5 m/s миттєвою швидкістю, виміряною спостерігачем на землі. Вилочний навантажувач, розташований на ліжку плоскоївагона, рухається зі швидкістю3 m/s, виміряною спостерігачем, що сидить на рухомому літаку. Обидва спостерігачі бачать лівий і правий напрямки аналогічно.
Визначити абсолютну швидкість навантажувача, тобто швидкість навантажувача, виміряну спостерігачем на землі,
(а) якщо спостерігач, що сидить на плоскій машині, бачить навантажувач рухається ліворуч від неї і
(б) якщо спостерігач, що сидить на плоскій машині, бачить навантажувач рухається праворуч від неї.
Рішення
Наступне рівняння визначає відносну швидкість навантажувача щодо плоского вагона:Vforklift / flat car=Vforklift−Vflatcar→Vforklift=Vflatcar+Vforklift / flatcar
Тепер припустимо, що позитивна вісь для нашої системи координат вказує праворуч.
(а)
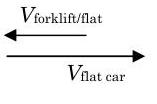
Малюнок5.1.5: Вилочний навантажувач рухається вліво, як спостерігає спостерігач на плоскому автомобілі.
→+Vforklift=Vflatcar−Vforklift / flatcar=(5 m/s)−(3 m/s)=2 m/sVforklift=2 m/s to the right.
(б)
.png)
Малюнок5.1.6: Вилочний навантажувач рухається вправо, як спостерігає спостерігач на плоскому автомобілі.
→+Vforklift=Vflatcar+Vforklift / flatcar=(5 m/s)+(3 m/s)=8 m/sVforklift=8 m/s to the right.
5.1.2 Як лінійний імпульс може зберігатися в системі?
Лінійний імпульс зберігається в русі маси системи; Таким чином, будь-яка система, яка має масу, має здатність зберігати лінійний імпульс. Оскільки це велика властивість, лінійний імпульс системи можна знайти, склавши лінійний імпульс кожної маси всередині системи. Для системи, що складається зN частинок, лінійний імпульс системиPsys знаходить шляхом підсумовування лінійного імпульсуN частинок в системі,Psys=N∑j=1Pj=N∑j=1mjVj
Для безперервної системи це підсумовування виконується за допомогою інтеграла над об'ємом системи:Psys=∫V−sys(Vρ) dV− де в цілому швидкість і щільність можуть змінюватися як в залежності від часу, так і положення.
Центр маси
Для обчислення лінійного імпульсу для розширеної системи, тобто чогось іншого, ніж частинки, необхідно оцінити інтеграл в еквалайзері. 5.1.15. На щастя, цей процес можна значно спростити, ввівши поняття центру мас. Центр маси - це точка, де вся маса для системи може бути зосереджена для цілей обчислення лінійного імпульсу. Як ми покажемо пізніше, це робить оцінку лінійного імпульсу простішим завданням.
Швидкість центру масVG, визначається наступним рівнянням:Psys=msysVG≡∫V−sys(Vρ) dV−→VG=1msys∫V−sys(Vρ) dV− Таким чином, швидкість центру мас дорівнює лінійному імпульсу системи, поділеному на масу системи.
Положення центру маси - це середньозважений по масі положення всієї маси всередині системи:rG=1msys∫V−sysrρ dV− На поверхні землі розташування центру мас по суті таке ж, як розташування центру ваги.rG З досвіду ми знаємо, що об'єкт, підвішений до свого центру ваги, не має схильності до обертання, тобто він ідеально збалансований. Коли щільність системи рівномірна, розташування центру мас ідентично центроїду об'єму системи. Розташування центроїда для найбільш поширених фігур було зведено в таблицю і можна знайти в математичних та фізичних підручниках.
Система складається з трьох частинок з масою, швидкістю і положеннями, як зазначено в таблиці.
| Частинка | m (kg) | r (m) | V (m/s) |
|---|---|---|---|
| 1 | \ (m\\ text {(кг)}\) ">15 | \ (\ mathbf {r}\\ текст {(м)}\) ">3i+3j | \ (\ mathbf {V}\\ текст {(м}/\ текст {s)}\) ">5i+5j |
| 2 | \ (m\\ text {(кг)}\) ">10 | \ (\ mathbf {r}\\ текст {(м)}\) ">−4i+2j | \ (\ mathbf {V}\\ текст {(м}/\ текст {s)}\) ">3i−5j |
| 3 | \ (m\\ text {(кг)}\) ">5 | \ (\ mathbf {r}\\ текст {(м)}\) ">1i+2j | \ (\ mathbf {V}\\ текст {(м}/\ текст {s)}\) ">2i−2j |
Визначте для системи наступне:
(а) Лінійний імпульс, вkg⋅m/s.
(b) Швидкість центру мас, вm/s.
(c) Розташування центру мас, вm.
Рішення
Відомий: Опис системи з відповідною інформацією
Знайти: Обчисліть лінійний імпульс для кожної системи.
Дано: Див. Нижче в кожному прикладі.
Аналіз
(а) Використовуйте визначення лінійного імпульсу.
Psys=P1+P2+P3=m1V1+m2V2+m3V3=(15 kg)[(5 ms)i+(5 ms)j]+(10 kg)[(3 ms)i−(5 ms)j]+(5 kg)[(2 ms)i−(2 ms)j]=[(75+30+10)i+(75−50−10)j](kg⋅ms)=(115i+15j)(kg⋅ms) or (115 kg⋅ms)i+(15 kg⋅ms)j
(b) Використовуйте визначальне рівняння для швидкості центру мас
(c) Використовуйте визначальне рівняння для розташування центру мас
Площинний рух твердого тіла
Багато фізичних систем, що представляють інтерес, можуть бути змодельовані як жорстке тіло. R igid тіло - це тіло, яке не деформується, тобто відносна відстань між будь-якими двома точками на тілі залишається постійною.
У цьому курсі ми обмежимо більшість наших дискусій тим, що називається рухом площини. Рух площини відбувається, коли будь-яка точка тіла рухається в площині, а площини, утворені локусом кожної точки в тілі, паралельні загальній опорній площині. Плоский рух твердого тіла можна класифікувати як трансляцію, обертання навколо нерухомої осі або загальний рух площини, що представляє собою комбінацію перекладу і обертання; див. Рис.5.1.7:
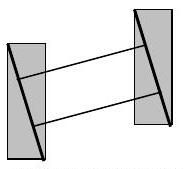 а) Прямолінійний переклад
а) Прямолінійний переклад.jpg) б) Криволінійний переклад
б) Криволінійний переклад
.jpg) в) Обертання навколо осі
в) Обертання навколо осі.jpg) г) Загальний рух площини
г) Загальний рух площини- Переклад. Якщо будь-яка пряма лінія всередині тіла залишається паралельною собі під час руху тіла, ми говоримо, що рух тіла є трансляцією. Якщо точка в тілі також слідує за прямою лінією, ми говоримо, що рух є прямолінійним перекладом. Якщо з іншого боку, точка в тілі слідує вигнутим шляхом, ми говоримо, що рух є криволінійним перекладом. Швидкість для кожної точки тіла, що перекладається, записується в прямокутних координатах якV=Vxi+Vyj.
- Обертання навколо нерухомої осі. Якщо всі точки в жорсткому тілі рухаються в паралельних площині і слідують за концентричними колами близько тієї ж нерухомої осі, ми говоримо, що тіло обертається навколо нерухомої осі. Фіксовану вісь називаємо віссю обертання. У цих умовах швидкість кожної точки в тілі може бути описана співвідношеннямV=rωeθ=rω(−(sinθ)i+(cosθ)j)
- Загальний рух площини. Досвід показав, що плоский рух будь-якого твердого тіла можна описати як комбінацію обертання твердого тіла навколо транслюючої осі обертання.
Кінематика загального руху площини ускладнена і її вивчення буде відкладено до подальшого курсу. Більшу частину часу ми будемо витрачати на вирішення прямолінійного перекладу та обертання навколо нерухомої осі. Через це вам важливо вміти ідентифікувати три типи плоского руху.
5.1.3 Як лінійний імпульс можна транспортувати через межу системи?
Лінійний імпульс може транспортуватися через межу системи двома різними механізмами: силами та масовим потоком. Як і у випадку з лінійним імпульсом, як сили, так і масові транспорти лінійного імпульсу є векторами, і для визначення кожного потрібно вказати величину, напрямок (сенс і лінію дії) та точку застосування.
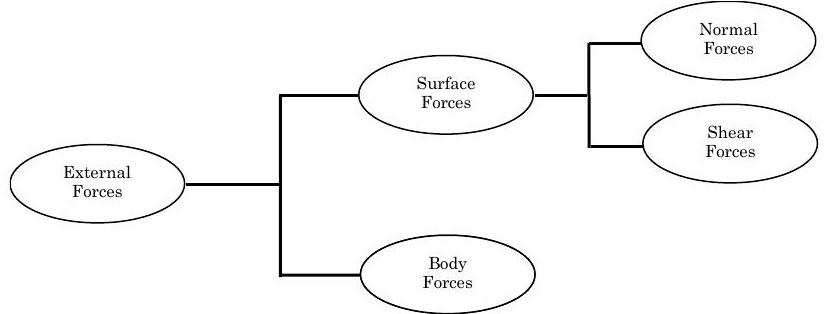
Малюнок5.1.8: Класифікація зовнішніх сил
Транспорт лінійного імпульсу з силою
Досвід показав, що лінійний імпульс замкнутої системи може бути змінений тільки за допомогою застосування зовнішньої сили (саме так Ньютон спочатку заявив свій другий закон). Таким чином, зовнішня сила, прикладена до замкнутої системи, повинна передавати лінійний імпульс між системою та її оточенням. Більш конкретно,Fexternal≡˙PForce={ transport rate of linear momentum across a boundary due to a force } де напрямок імпульсного потоку знаходиться в тому ж напрямку, що і сила.
Зовнішня сила - це механізм передачі лінійного імпульсу і є транспортною швидкістю для лінійного імпульсу через межу між системою та її оточенням. Сила - це вектор з усіма властивостями, розглянутими раніше. Первинними розмірами для сили є[M][L]/[T]2, які є розмірами [Лінійний імпульс]/[Час]. Типовою одиницею сили є ньютон(N) в СІ і фунт-сила(lbf) в USCS.
Коли кілька сил діють на систему, чиста швидкість перенесення лінійного імпульсу в систему із зовнішніми силами записується математично, як показано нижче:∑jFext j≡{net transport rate of linear momentuminto the system with force} Зовнішні сили, як показано на малюнку5.1.8, можна класифікувати як поверхневі сили, так і сили тіла. Поверхневі сили можна додатково класифікувати як нормальні, так і зсувні сили.
Сили тіла
Сила тіла завжди діє розподілено в об'ємі системи і є результатом розміщення системи в силовому полі, наприклад, гравітаційному полі, електричному полі або магнітному полі. Через це тіло силу іноді називають «силою на відстані». Оскільки він діє над обсягом системи, сила тіла може бути розрахована лише після визначення системи.
Найпоширенішою силою тіла є вага - сила, що чиниться Землею на масу, розміщену в гравітаційному полі Землі. Хоча сила тіла діє по всій системі, її ефект часто представлений як зосереджена сила, яка діє в певній точці всередині системи. Коли напруженість поля просторово рівномірна, як і в гравітаційному полі Землі, вважається, що вага об'єкта діє в центрі ваги системи. Біля поверхні Землі, коли об'єкт підвішений до свого центру ваги, об'єкт буде ідеально збалансований.
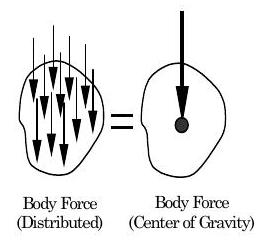
Малюнок5.1.9: Сила тіла внаслідок сили тяжіння
Визначте величину, напрямок і точку застосування вектора ваги для систем A, B і C. Кожна система виготовлена з матеріалу з щільністю900 kg/m3. У кожному конкретному випадку накидайте свою систему і знайдіть центр ваги. [Підказка: Ви можете спробувати свою книгу фізики, обчислення або хорошу таблицю математики, щоб знайти розташування центроїда цих томів.]
| Система А | Система B | Система C |
|---|---|---|
| Правий круглий циліндр діаметромD=20 cm і висотоюH=40 cm. |
Правильний круглий конус діаметромD=20 cm і висотоюH=40 cm. |
Півсфера діаметраD=20 cm. |
Поверхневі сили
Поверхнева сила характеризується наявністю точки або точок фізичного контакту на граничній поверхні, і з цієї причини її іноді називають контактною силою. Фізично поверхневі сили завжди діють над кінцевою площею, тобто вони є розподіленими силами.
Зазвичай ми зазвичай представляємо поверхневі сили єдиною зосередженою силою (див. Рис.5.1.10). Коли поверхнева сила діє на плоску поверхню і або площа невелика, або сила рівномірно розподілена по площі, розумно моделювати розподілену силу як єдину зосереджену силу з точкою прикладання в центроїді області.
.png)
Малюнок5.1.10: Поверхневі сили
Коли поверхня вигнута або розподілена сила неоднорідна, єдина зосереджена сила все ще може бути використана для моделювання розподіленої сили; однак точна точка застосування повинна бути ретельно обчислена і не обов'язково є центроїдом області, над якою діє розподілена сила.
Кожна поверхнева сила при необхідності може бути додатково розкладена на дві складові: нормальну і зсувну складову, як показано на малюнку5.1.11. Лінія дії нормальної сили перпендикулярна поверхні в точці прикладання, а лінія дії сили зсуву дотична до поверхні в точці прикладання. Деякі зовнішні сили за своєю природою є чисто нормальними або чисто зсувними силами. Наприклад, сила, що створюється тиском атмосфери на будь-якій поверхні, завжди є нормальною силою, тоді як сила, обумовлена тертям, завжди є силою зсуву.
.png)
Малюнок5.1.11: Нормальні та зсувні сили.
Поверхневі сили через тиск
Однією з найбільш повсюдних сил в нашому житті є сила атмосфери. Через це ми повинні розглянути, як визначити поверхневі сили, обумовлені тиском. За визначенням тиск визначається як сила на одиницю площі. Розміри для тиску є[F]/[L]2={[M][L]/[T]2}/[L]2=[M][L]−1[T]−2. Типовими одиницями тиску є ньютон на квадратний метр або паскалі(Pa) в СІ с1 Pa=1 N/m2. У USCS одиниці є фунтів-сила на квадратний дюйм (psiабоlbf/in2) або фунтів-сила на квадратний фут (psfабоlbf/ft2) с144 psi=144 lbf/in2=1 lbf/ft2.
Стандартне значення атмосферного тиску на поверхню землі становитьPatm=101325 Pa=101.325 kPa=14.696 lbf/in2. Ці значення часто округляються до101.3 kPa і14.7lbf/in2.
Щоб оцінити силу через тиск, що діє на поверхню, ми повинні спочатку визначити поверхню (див. Рис.5.1.12). Математично сила розраховується за допомогою інтеграла тиску над площею поверхні, як показано нижче:
Fpressure=−∫AsurfacenP dAдеP - тиск, що діє на межі,n - одиничний нормальний вектор, який вказує з системи в оточення, іdA являє собою диференціальну область, над якою діє тиск. Таким чином, напрямок сили тиску завжди знаходиться в систему.
.jpg)
Малюнок5.1.12: Геометрія для розрахунку сили тиску.
Найпростішим, а також найпоширенішим застосуванням є те, де тиск рівномірний, а поверхня рівна. За цих умов Eq. 5.1.20можна значно спростити, оскільки і одиничний нормальний вектор, і тиск виходять за межі інтеграла:
Fpressure=−∫AsurfacenP dA=−(nP)∫AsurfacedA⏟=Asurface=−PAsurfacen
На словах це говорить про те, що сила тиску на рівну поверхню за рахунок рівномірного тиску є вектором, який перпендикулярний поверхні, вказує в систему, і має величинуPAsurface, , рівну, добутку тиску і площі поверхні. Крім того, можна показати (після вивчення кутового моменту), що точка прикладання сили знаходиться в центрі площі поверхні.
Як приклад розглянемо трикутне тверде тіло з постійною шириною в папір, як показано на малюнку5.1.13. Рівномірний тиск діє на кожну з трьох сторін, як показано на малюнку. Оскільки кожен тиск рівномірний, а поверхні плоскі, еквівалентний вектор сили тиску можна обчислити за допомогою Eq. 5.1.21. Для кожної сторони вектор сили вказує на поверхню, є нормальним до поверхні і має величину, рівну добутку тиску і площі поверхні, на яку діє рівномірний тиск.
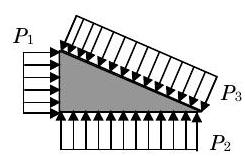 а) Розподіл тиску
а) Розподіл тиску.jpg) б) Вектори сили тиску
б) Вектори сили тискуНерідко у нас будуть системи, які піддаються атмосферному тиску по всій межі системи. Уявіть на хвилину який-небудь конкретний предмет, який вам хотілося б, скажімо, ваш автомобіль або яблуко, що висить на нитці, тобто піддається рівномірному атмосферному тиску з усіх боків. Яка чиста сила атмосфери на об'єкт? Виходячи з вашого досвіду, я припускаю, ви б сказали, що чиста сила через тиск атмосфери дорівнює нулю. Ви можете повторити цей експеримент, і ви виявите, що чиста сила на будь-якому об'єкті, оточеному рівномірним тиском, буде дорівнює нулю незалежно від форми предмета або значення тиску.
Це призводить нас до ще одного цікавого результату. Розглянемо суцільне тіло неправильної форми, показане на малюнку5.1.14. Уявіть, що об'єкт піддається рівномірному тиску з усіх боків і що отримані вектори сили тиску показані на малюнку. Тепер ми знаємо з досвіду, що якщо єдині сили обумовлені рівномірним тиском, то чиста сила на об'єкт через тиск відсутня. Якби це не було правдою, то об'єкт мав би тенденцію до переміщення (а ми б запатентували цей пристрій і пішли на Кариби). Це повинно означати, що сила тиску, що діє на ліву сторону твердого тіла, повинна дорівнювати сумі сил тиску, що діють над правою стороною твердого тіла. Як ми показали, сила тиску пропорційна площі поверхні. Так чому ж ліва сторона не має більше сили тиску, ніж права сторона? Ключ полягає в векторному характері сили.
.jpg)
Малюнок5.1.14: Сили тиску з використанням проектованих ділянок.
Щоб допомогти нам зрозуміти цей результат, давайте тільки розглянемо силу вx -напрямку. Тепер ми бачимо, що сила тиску, що діє над лівою стороною твердого тіла, повинна дорівнюватиx -складових сил тиску, що діють на праву сторону твердого тіла. Не вдаючись до складної математики, ми можемо підсумувати цей результат наступним чином:
Величина сили тиску в будь-якому напрямку дорівнює добутку тиску і проектованої площі в потрібному напрямку.
Проектована площа - це двовимірна площа, що спостерігається при розгляді поверхні в цікавому напрямку. Розглянемо сферу з діаметромD і циліндр з діаметромD і висотоюH. При спостереженні з будь-якого напрямку сфера виглядає як коло з проектованою площеюπD2/4. Тепер розглянемо циліндр. При погляді з будь-якого кінця циліндр також має проектовану площуπD2/4; однак, якщо дивитися збоку (перпендикулярно до його осі симетрії), проектована площа циліндра є прямокутником площіDH.
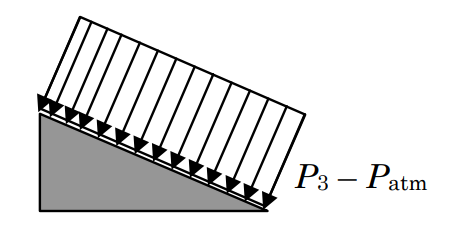
У нас також часто виникнуть проблеми, коли лише невелика частина межі системи піддається неатмосферному тиску. У цих умовах ми можемо значно спростити розрахунки сили тиску, «віднімаючи» атмосферний тиск. Розглянемо знайоме трикутне тверде тіло, як показано на малюнку5.1.15.
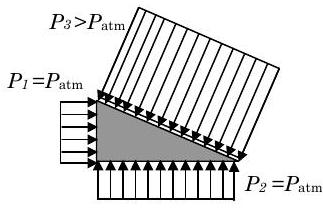
.jpg)
.png)
в) Отриманий розподіл тиску з
P3,new=P3−Patm
Fnet=−(P3−Patm)A3n
Для цього прикладу будемо вважати, що всі поверхні, крім однієї, піддаються атмосферному тиску і ця поверхня має рівномірний тискP3>Patm. Як показано на малюнку, ми можемо використовувати стандартний інтеграл для оцінки чистої сили, обумовленої тиском, що діють на систему. Оскільки чиста сила, обумовлена рівномірним атмосферним тиском на всіх поверхнях, дорівнює нулю, як показано в частині (b) малюнка,5.1.15 ми можемо відняти цю нульову силу від інтеграла. Як тільки це буде зроблено, інтеграл для чистої сили може бути перебудований, як показано, і ми виявляємо, що чиста сила є результатом тиску, виміряного щодо атмосферного тиску (це іноді називають манометричним тиском). Нарешті, як показано в частині (c) величина чистої сили справедлива(P3−Patm)A3. Так якP3>Patm, сила стрілка вказує на поверхню 3. Коли якась частина кордону системи піддається неатмосферному тиску, віднімання атмосферного тиску значно спростить розрахунок сили чистого тиску.
Щоб дати нам деяку швидку практику з цими ідеями, розглянемо помічника сантехніка, який використовується для відчищення туалетів. Помічник класичного сантехніка складається з порожнистої гумової півсфери, прикріпленої до дерев'яної палиці. Гумовий матеріал гнучкий і деформується при натисканні на поверхню. Якщо наносити його на гладку поверхню, як показано на малюнку, повітря буде видавлюватися з півсфери. Це знижує тиск всередині деформованої півсфери і змушує помічника сантехніка «прилипати» до поверхні. Яка саме сила сітки у вертикальному напрямку через тиск на помічника сантехніка?
.png)
Малюнок5.1.16: Помічник сантехніка.
Рішення
Розглянемо систему, показану вище пунктирними лініями. Чашка, що контактує з поверхнею, має діаметрD. Тиск на кожну поверхню системи, крім відкритого кінця гумової чашки (верхньої поверхні), піддається атмосферному тиску,Patm. Поверхня, яка покриває відкритий кінець чашки, бачить тискPcup - тиск повітря, захопленого всередині деформованої півсфери.
Проектована площа помічника сантехніка, якщо дивитися зверху або знизу по вертикалі, - це всього лише коло з площею(π/4)D2. Крім того, оскільки ми хочемо знайти чисту силу, ми можемо просто відняти атмосферний тиск.
Таким чином
Fnet pressure=−(Pcup−Patm)Aprojectedn↑+Fnet pressure=−(Pcup−Patm)(π4D2)(1)=(Patm−Pcup)(π4D2)Fnet pressure=(Patm−Pcup)(π4D2)∠90∘ or (Patm−Pcup)(π4D2)↑
Як і слід було очікувати\boldsymbol{P_{\text {cup}}<P_{\text {atm}}, якщо чиста сила буде вгору (уy позитивному напрямку). Є принаймні дві інші сили, що діють на цю систему, які будуть регулювати, чи «прилипає» чи падає - вага системи та сила гладкої поверхні на системі, де вона контактує з гумовою півсферою.
Лінійний транспорт імпульсу з масовим потоком
Як було показано раніше, кожна грудка маси зі швидкістю має лінійний імпульс. Коли масі дозволяється протікати через межу відкритої системи, кожна грудка маси несе з собою лінійний імпульс. Таким чином, лінійний імпульс відкритої системи також може бути змінений масовим потоком, що несе лінійний імпульс через межу системи. Швидкість, з якою лінійний імпульс транспортується через межу, може бути представлена добутком масової витрати та місцевої швидкості на кордоні, припускаючи, що швидкість рівномірна:\dot{\mathbf{P}}_{\text {mass}} = \dot{m} \mathbf{V} = \left\{\begin{array}{c} \text { transport rate of linear momentum } \\ \text { with mass flow } \end{array}\right\} \nonumber де\dot{m} масова витрата на межі потоку, де швидкість\mathbf{V} рівномірний. Розмірність для цієї величини є[\mathrm{M}][\mathrm{L}] /[\mathrm{T}]^{2}.
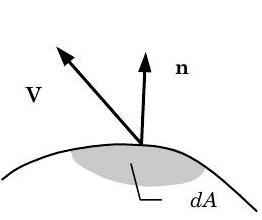
Рисунок\PageIndex{17}: Масовий транспорт лінійного імпульсу на межі.
Для умов, коли швидкість не є просторово рівномірною на межі потоку, швидкість перенесення лінійного імпульсу повинна бути розрахована з використанням інтеграла. На будь-якій межі потоку, як показано на малюнку\PageIndex{17}, перенесення лінійного імпульсу з системи можна охарактеризувати інтегралом:\begin{array} \dot{\mathbf{P}}_{\text {mass, out}} &= \displaystyle \int\limits_{A_{\text {sys}}}(\mathbf{V}) \left( \rho \mathbf{V}_{\text {rel}} \cdot \mathbf{n} \right) \ dA \\ &= \displaystyle \int\limits_{A_{\text {sys}}}(\mathbf{V}) \left(\rho V_{\text {n, rel}}\right) \ dA \end{array} \nonumber де\mathbf{V} локальний вектор швидкості, виміряний відносно інерційної системи відліку,\mathbf{V}_{\text{rel}} - локальний вектор швидкості, виміряний за допомогою по відношенню до поверхні,\mathbf{n} є одиничним вектором нормаль до диференціальної площі поверхніd A і вказує з системиV_{\text{n, rel}} = \mathbf{V}_{\text {rel}} \cdot \mathbf{n}, причому, величину нормальної складової швидкості\mathbf{V}_{\text {rel}}.
Якщо швидкість просторово рівномірна на перерізі потоку, масовий транспорт лінійного імпульсу можна записати через масову швидкість потоку на кордоні та швидкість наступним чином:
\begin{align} \dot{\mathbf{P}}_{\text{mass, out}} &= \int\limits_{A_{\text{sys}}} (\mathbf{V}) \left( \rho V_{\text{n, rel}} \right) \ dA = (\mathbf{V}) \left( \rho V_{\text{n, rel}} \right) \int\limits_{A_{\text{sys}}} dA \nonumber \\[4pt] &= (\mathbf{V}) \left( \rho V_{\text{n, rel}} \right) A_{\text{sys}} = \left( \rho V_{\text{n, rel}} A_{\text{sys}} \right) \mathbf{V} \\ &= \dot{m}_{\text{out}} \mathbf{V} \nonumber \end{align} \nonumber
Це часто називають одновимірним потоком. Якщо швидкість не є рівномірною по всій площі потоку, площа потоку повинна бути розбита на відповідну кількість областей, де швидкість можна вважати рівномірною і Eq. \PageIndex{24}стане підсумовуванням. Крім того, нерівномірний розподіл швидкості може бути оброблений, виконуючи інтеграл в Eq. \PageIndex{23}.
Чистий транспорт лінійного імпульсу з масовою швидкістю потоку можна отримати шляхом підсумовування транспортів на всіх границях потоку:\sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} \equiv \left\{ \begin{array}{c} net \text { transport rate of linear momentum } \\ into \text { the system with mass flow } \end{array}\right\} \nonumber Зверніть увагу, що чистий транспорт може бути позитивним або негативним залежно від відносних перевезень.
5.1.4 Як лінійний імпульс може генеруватися або знищуватися в системі?
Досвід показав, що лінійний імпульс системи не може бути створений або знищений. Визнаючи, що лінійний імпульс є великою властивістю, ми можемо констатувати цей закон наступним чином:
Лінійний імпульс - це збережена властивість.
Ще раз вам нагадують, що вживання слова «збереження» в цьому курсі (ES201) відрізняється, ніж ви знайомі з фізикою. (Давай, погляньте на свою книгу з фізики і подивіться, які проблеми вони вирішують в розділі з назвою «збереження лінійного імпульсу». Чи відрізняються проблеми збереження енергії від проблем збереження лінійного імпульсу?) У цьому курсі, коли ми говоримо, що щось збережено, ми робимо загальне твердження про те, як поводиться світ, а не проблема конкретного моделювання припущення. Насправді, можна сказати, що некоректно (якщо не надмірно) писати у вирішенні проблеми «припустимо, що лінійний імпульс (або маса або заряд) зберігається». Ви не можете посилатися на основні фізичні закони, припускаючи їх існування. Було б правильно сказати «використовуючи (або застосовуючи) збереження лінійного імпульсу (або маси або заряду), ми виявляємо, що...» Основні фізичні закони застосовуються, хочемо ми їх чи ні.
5.1.5 Збираємо все разом!
Використовуючи систему бухгалтерського обліку, тепер ми можемо розробити наступне твердження для збереження лінійного імпульсу:\left[ \begin{array}{c} \text { Rate of accumulation } \\ \text { of } \\ \text { linear momentum } \\ \text { inside a system } \\ \text { at time } t \ \end{array} \right] = \left[ \begin{array}{c} \text { Net transport rate of } \\ \text { linear momentum } \\ \text { into the system } \\ \text { by external forces } \\ \text { at time } t \ \end{array}\right] + \left[\begin{array}{c} \text { Net transport rate of } \\ \text { linear momentum } \\ \text { into the system } \\ \text { by mass flow } \\ \text { at time } t \ \end{array}\right] \nonumber або в символах збереження лінійного імпульсу (форма швидкості) стає\frac{d \mathbf{P}_{\text {sys}}}{d t} = \sum \dot{\mathbf{P}}_{\text {force}} + \sum_{\text {in}} \dot{\mathbf{P}}_{\text {mass, in}} - \sum_{\text{out}} \dot{\mathbf{P}}_{\text {mass, out}} \nonumber
Використовуючи більш звичні символи сил, масових витрат та питомого лінійного імпульсу, форма швидкості збереження лінійного імпульсу стає\frac{d \mathbf{P}_{\mathrm{sys}}}{d t} = \sum \mathbf{F}_{\text {ext}} + \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} \label{RateFormLN} Словами, ми можемо сказати наступне:
Часова швидкість зміни лінійного імпульсу системи дорівнює чистої швидкості транспортування лінійного імпульсу в систему зовнішніми силами плюс чиста швидкість транспортування лінійного імпульсу в систему масовим потоком.
За деяких умов корисна інтегрована або скінченно-часова форма. На словах скінченно-часова форма збереження лінійного імпульсу дорівнює \left[ \begin{array}{c} \text { Linear } \\ \text { momentum } \\ \text { inside the } \\ \text { system at } \\ \text { time } t_{2} \end{array}\right] - \left[\begin{array}{c} \text { Linear } \\ \text { momentum } \\ \text { inside the } \\ \text { system at } \\ \text { time } t_{1} \end{array}\right] = \left[\begin{array}{c} \text { Net transport of } \\ \text { linear momentum } \\ \text { into the system } \\ \text { by external forces } \\ \text { during the period } \Delta t \end{array}\right]+\left[\begin{array}{c} \text { Net transport of } \\ \text { linear momentum } \\ \text { into the system } \\ \text { by mass flow } \\ \text { during the period } \Delta t \end{array}\right] \nonumber
або у формі рівняння,\Delta \mathbf{P}_{\mathrm{sys}} = \sum_{\text {external}} \left( \int\limits_{t_{1}}^{t_{2}} \mathbf{F} \ dt \right) + \sum_{\text {in}} \left( \int\limits_{t_{1}}^{t_{2}} \left(\dot{m}_{i} \mathbf{V}_{i}\right) \ d t \right) - \sum_{\text {out}} \left(\int\limits_{t_{1}}^{t_{2}} \left(\dot{m}_{e} \mathbf{V}_{e}\right) \ dt \right) \nonumber Хоча ця остання форма збереження лінійного рівняння імпульсу виглядає досить складною, насправді набагато простіше зосередитися на формі швидкості, а потім, якщо необхідно, виконати необхідну інтеграцію для відновлення Рівняння\PageIndex{30}.
Закони Ньютона зазвичай пишуться наступним чином:
Закон I: Якщо результуюча сила, що діє на частинку, дорівнює нулю, частка залишиться в стані спокою (якщо спочатку знаходиться в стані спокою) або буде рухатися з постійною швидкістю по прямій лінії (якщо спочатку в русі)
Закон II: Якщо результуюча сила, що діє на частинку, не дорівнює нулю, частка матиме прискорення, пропорційне величині результуючої сили і в напрямку цієї результуючої сили
Закон III: Сили дії та реакції між тілами, що контактують, мають однакову величину, однакову лінію дії та протилежний сенс.
Продемонструйте, що ці три закони задовольняються застосуванням форми швидкості збереження лінійного імпульсу.
Рішення
Відомий: три закони механіки Ньютона
Знайти: Показати, що ці закони підтримуються збереженням лінійного імпульсу
Дано: Надається в міру необхідності.
Аналіз:
Перший закон Ньютона: Подивіться на одну частинку, як показано на малюнку. Щоб застосувати збереження лінійного імпульсу, ми вибираємо частинку як систему і намалюємо діаграму лінійної взаємодії імпульсу (вільного тіла) для тіла.
.png)
Малюнок\PageIndex{18}: Система, що складається з частинки. Діаграма вільного тіла цієї системи, яка не має взаємодій з її оточенням.
Записуючи швидкість форми збереження лінійного імпульсу для цієї системи ми маємо:
\begin{align*} &\frac{d \mathbf{P}_{\text{sys}}}{dt} = \underbrace{ \cancel{ \sum \mathbf{F}_{\text{ext}} } }_{ \begin{array}{c} =0 \text{ because there} \\ \text{are no external} \\ \text{forces} \end{array} } + \underbrace{ \cancel{ \sum_{\text{in}} \dot{m}_i \mathbf{V}_i - \sum_{\text{out}} \dot{m}_e \mathbf{V}_e } }_{\begin{array}{c} =0 \text{ because} \\ \text{it is a closed system} \end{array} } \\ &\frac{d \mathbf{P}_{\text{sys}}}{dt} = 0 \quad \rightarrow \quad 0 = \frac{d \mathbf{P}_{\text{sys}}}{dt} = \frac{ d (m \mathbf{V})}{dt} = m \frac{d \mathbf{V}}{dt} \end{align*} \nonumber
Таким чином,\dfrac{d \mathbf{V}}{dt} = 0 і\mathbf{V} є постійною!
Це демонструє, що при відсутності транспортів лінійного імпульсу силою, тобто при відсутності зовнішніх сил, що діють на частинку, швидкість частинки залишається постійною.
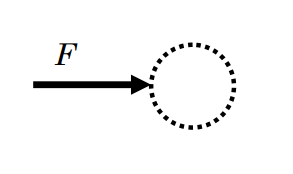
Другий закон Ньютона: Система така ж, як і раніше, тільки на цей раз на систему діє сила.
.png)
Малюнок\PageIndex{19}: Діаграма вільного тіла системи, що складається з частинки з діючою на неї силою.
\begin{align*} &\frac{d \text{P}_{\mathrm{sys}}}{dt} = \mathbf{F} + \underbrace{ \cancel{ \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} } }_{\begin{array}{c} =0 \text { because } \\ \text { it is a closed system } \end{array} } \\ &\frac{d \mathbf{P}_{\text {sys}}}{d t} = \mathbf{F} \quad \rightarrow \quad \mathbf{F} = \frac{d \mathbf{P}_{\text {sys}}}{d t} = \frac{d(m \mathbf{V})}{d t} = m \underbrace{\frac{d \mathbf{V}}{d t}}_{= \mathbf{a}} = m \mathbf{a} \end{align*} \nonumber
Таким чином\mathbf{F}=m \mathbf{a} і\mathbf{a}=\mathbf{F} / m.
Це демонструє, що вектор прискорення пропорційний вектору зовнішньої сили, тому величина прискорення пропорційна прикладеної сили і напрямок таке ж, як напрямок прикладеної сили.
Третій закон Ньютона: Цього разу наша система є інтерфейсом або поверхнею контакту між двома частинками, які контактують. Цей інтерфейс, як показано на малюнку нижче, не має маси всередині нього і діє на нього дві сили -\mathbf{F}_{\mathrm{A-B}}, сила частинки\mathrm{A} на частинку\mathrm{B}, і\mathbf{F}_{\mathrm{B-A}}, сила частинки\mathrm{B} на частку\mathrm{A}.
.png)
Малюнок\PageIndex{20}: Система, що складається з контактного інтерфейсу між двома частинками.
Запис збереження лінійного рівняння імпульсу для цієї системи дає наступне:
\begin{align*} \underbrace{ \cancel{ \frac{d \mathbf{P}_{\text{sys}}}{dt} } }_{\begin{array}{c} =0 \text{ because the system} \\ \text{has no mass, so } \mathbf{P} = 0 \\ \text{for all time.} \end{array} } = \mathbf{F}_{\text{A-B}} + \mathbf{F}_{\text{B-A}} + \underbrace{ \cancel{ \sum_{\text{in}} \dot{m}_i \mathbf{V}_i - \sum_{\text{out}} \dot{m}_e \mathbf{V}_e } }_{\begin{array}{c} =0 \text{ because} \\ \text{it is a closed system} \end{array}} \\ 0 = \mathbf{F}_{\text{A-B}} + \mathbf{F}_{\text{B-A}} \quad \rightarrow \quad \mathbf{F}_{\text{B-A}} = -\mathbf{F}_{\text{A-B}} \end{align*} \nonumber
Таким чином, сили дії і реакції в точці зіткнення двох систем - вектори рівної величини, протилежного знака і однієї лінії дії.
Коментар: Важливим моментом тут є те, що всі три закони механіки Ньютона включені в принцип збереження лінійного імпульсу, як сформульовано тут.
