5.2: Збереження лінійного рівняння імпульсу
Рекомендованою відправною точкою для будь-якого застосування збереження лінійного імпульсу є форма швидкості лінійного рівняння імпульсу (раніше наведено як Рівняння (5.1.28):dPsysdt=∑Fext+∑in˙miVi−∑out˙meVe деPsys система лінійний імпульс,Fext - швидкість перенесення лінійного імпульсу зовнішньою силою, і˙mV це швидкість транспортування лінійного імпульсу масовим потоком.
Застосовуючи форму швидкості збереження лінійного імпульсу до системи, існує багато моделюючих припущень, які часто використовуються для побудови математичної моделі фізичної системи. Вони детально описані в наступних параграфах. Як завжди, ви повинні зосередитися на розумінні того, що означають припущення фізично і як вони можуть бути використані для спрощення рівнянь для даної системи. Не варто просто запам'ятовувати результати.
Сталий стан системи:
Якщо система працює в стаціонарних умовах, всі інтенсивні властивості не залежать від часу, тобто значення інтенсивних властивостей можуть змінюватися тільки в залежності від положення. Таким чином, лінійний імпульс системи є постійним,Psys=constant. Коли це припущення застосовується до збереження лінійного рівняння імпульсу, ми маємо
dPsysdt⏟Psys=constant=0=∑Fext+∑in˙miVi−∑out˙meVe0=∑Fext+∑in˙miVi−∑out˙meVeНа словах це говорить про те, що чиста швидкість транспортування лінійного імпульсу в систему силою повинна дорівнювати чистої швидкості транспортування лінійного імпульсу з системи масовим потоком.
Закрита система:
Система з кордонами, вибраними таким чином, щоб масова витрата на будь-якій межі була однаково нульовою, є замкнутою системою; таким чином маса системи постійна. При застосуванні до збереження лінійного імпульсу це припущення має наступний ефект:
dPsys=msysVGdt=∑Fext+∑in˙mi=0Vi−∑out˙me=0VemsysdVGdt+dmsysdt=0⏟ClosedsystemVG=∑FextmsysdVGdt=∑Fext
VGде - швидкість центру мас системи. Згадуючи, що прискорення - це всього лише похідна за часом швидкості, ми відразу визнаємо, що це наш старий друг з фізики:F=ma.
Закрита, стійка система:
Використовуючи те, що ви дізналися до цього моменту, як би ви очікували, що лінійне рівняння імпульсу спростить для замкнутої системи, яка працює в умовах сталого стану?
Застосовуючи збереження лінійного імпульсу для моделювання системи, нам потрібно, як завжди, вибрати систему та визначити транспорти лінійного імпульсу через межу системи. Рекомендації щодо малювання діаграми лінійного імпульсу (або вільного тіла) наведені нижче:
- Виберіть систему. Кожна система може бути розбита на менші підсистеми. Для даної проблеми може бути кілька можливих систем, і різні питання можуть вимагати іншої системи.
- Намалюйте фізичний об'єкт, чітко визначаючи межі вашої системи. Зазвичай це робиться пунктирною лінією для позначення межі системи.
- Від'єднайте систему від її оточення і намалюйте ізольований контур системи, тобто межі системи.
- Визначте транспорти імпульсу між системою та оточенням. При виявленні зовнішніх сил враховуйте тільки сили, що чинилися оточенням на систему. Пам'ятайте, що існує два типи зовнішніх сил: контактні (або поверхневі) сили, які діють на межі системи, і сили тіла, що виробляються такими полями, як гравітаційна сила, яку зазвичай називають вагою.
- Для кожного імпульсного транспорту намалюйте стрілку на системній схемі, що показує напрямок і місце розташування транспорту. Слід подбати про те, щоб намалювати кожну стрілку з правильним напрямком (лінією дії і сенсом) і положенням. Позначте всі сили та масові транспорти імпульсу назвою, номером або символом. Намалюйте вектор на схемі, розташувавши або хвіст, або голову стрілки в точці нанесення:
- Контактні сили слід прикладати у відповідній точці на кордоні системи, де система була «відрізана» від оточення.
- Вектор ваги слід наносити в центрі ваги тіла.
- Масовий транспорт лінійного вектора імпульсу слід застосовувати в точці, де маса перетинає межу і в напрямку швидкості.
- Якщо ви не знаєте правильного напрямку передачі імпульсу, припускайте напрямок. Якщо ваш аналіз призводить до негативного числового значення для передачі, то фактичний напрямок протилежний передбачуваному напрямку.
- Намалюйте систему координат і вкажіть всі відповідні розміри та кути на діаграмі вільного тіла.
Тенісист подає м'яч на відстаніL=40 ft назад від сітки і висотіH=9 ft над кортом. Тенісний м'яч залишає ракетку з кутомθ=0∘ нижче горизонталі, як показано на малюнку. Сітка3ft висока, а центр тенісного м'яча очищає сітку на 3 дюйми. Визначте (а) початкову швидкістьVo м'яча, коли він залишає ракетку і (б) відстаньs за сіткою, де м'яч потрапляє на майданчик. Припустимо, що опір повітря незначний. Маса тенісного м'яча становить0.25 lbm.
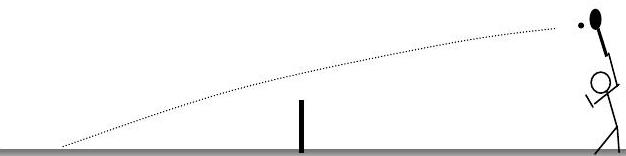
Малюнок5.2.1: Тенісист подає м'яч.
Рішення
Відомо: Тенісний м'яч подається з заданим кутом із зазначеного місця.
Знайти: (а) Швидкість м'яча, коли він перетинає сітку і (б) відстань від сітки, де він потрапляє на корт.
Дано:
.jpg)
Малюнок5.2.2: Діаграма, що вказує шлях, пройдений кулькою, присвоюється система координат і позначена всіма відповідними вимірами.
Аналіз:
Система→ Виберіть тенісний м'яч в якості системи. Це закрита система.
Властивість для підрахунку→ Оскільки траєкторія регулюється дією сили тяжіння, розраховуйте лінійний імпульс.
Період часу→ Зрештою потрібно інтегрувати протягом скінченного часу, щоб отримати траєкторію та швидкість.
Спочатку ми повинні намалювати діаграму вільного тіла (лінійного імпульсу) для системи. Єдині транспорти лінійного імпульсу відбуваються за рахунок сили тяжіння тіла - ваги. Інерційна система координат та інші розміри показані на малюнку5.2.2 вище.
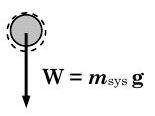.jpg)
Малюнок5.2.3: Діаграма вільного тіла системи.
Написання швидкості форми збереження лінійного імпульсу для системи дає
dPsysdt=W+[∑in˙miVi+∑out˙meVe]=0⏟Closed system, ˙m=0→ddt(msys VG)=msysdVGdt=msys g→msys dVGdt=msys g
Тепер пишемо рівняння в скалярній формі за допомогою системи координат, визначеної вищеVG=Vxi+Vyj, і ми маємо наступні рівняння:
msys dVGdt=msys g→ddt(Vxi+Vyj)=−gj→{x- axis: dVxdt=0y-axis: dVydt=−g
Інтеграція один раз, щоб отримати швидкість даєx-axis: dVxdt=0→Vx=constant=Vx,o=Vo(cosθ)→Vx=Vo(cosθ)y-axis: dVydt=−g→Vy∫Vy,odVy=−t∫0g dt→Vy−Vo(sinθ)=−gt→Vy=−gt+Vo(sinθ)
Тепер знову інтегруємо, щоб отримати позицію:x-axis: Vx=dxdt=Vocosθ→x∫0dx=t∫0(Vocosθ)⏟Constant dt→x=(Vocosθ)ty- axis: Vy=dydt=−gt−Vosinθ→y∫Hdx=−t∫0(gt+Vosinθ) dt→y−H=−(gt22+(Vosinθ)t)
Тепер, коли ми знаємо положення та швидкість як функцію часу, давайте спочатку вирішимо початкову швидкість, необхідну для очищення мережі приx=L іy=h+d.
Дляθ=0 withx іy як зазначено вище, у нас є два рівняння для двох невідомихt іVo:x-axis: L=Vot→ t=L/Voy-axis: (h+d)−H=−[12gt2]→t2=2g[H−(h+d)]
Поєднання цих рівнянь і усунення часуt дає наступний результат:
t2=(LVo)2=2g[H−(h+d)]V2o=gL22[H−(h+d)]→Vo=√gL22[H−(h+d)]=√(32.2 fts2)(40 ft)22[9−(3+312)]ft=66.9 fts
Тепер, щоб вирішити дляs, ми визнаємо, щоs=x−40 колиy=0 і використовувати два рівняння зміщення:s=x−(40 ft)=Vot−(40 ft)0−H=−12gt2→H=12gt2→s=Vo√2Hg−(40 ft)
Рішення для дистанціїs:s=(66.9 fts)√2(9 ft)(32.3 ft/s)−(40 ft)=10.0 ft
Коментарі:
- Припускаючи, що діаметр тенісного м'яча становить 3 дюйми, а теніс все ще б'є з початковою швидкістю, розрахованої вище, визначте максимальне значенняθ перед тим, як м'яч потрапить в сітку.
- Тепер визначте мінімальну початкову швидкість, яку повинен мати м'яч, щоб очистити сітку, якщо вона потрапила горизонтально, наприкладθ=0.
Вода стабільно тече через горизонтальну насадку, прикріплену до труби. Сопло фланцеве і кріпиться до труби за допомогою 6 болтів, як показано на малюнку. Труба і впускний патрубок має внутрішній діаметр25 cm і вихідний діаметр сопла12 cm. Абсолютний тиск на вході в сопло є500 kPa і швидкість води дорівнює5 m/s. Тиск на виході з сопла - атмосферний тиск(Patm=100kPa). Припустимо, що щільність рідкої води є1000 kg/m3.
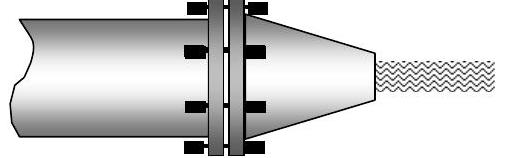
Малюнок5.2.4: Вода рухається по циліндричній трубі, прикріпленої до фланцевому патрубку.
Визначте загальну силу, в ньютонах, прикладену болтами, щоб утримувати сопло на місці. Припустимо, що болти підтримують тільки натяг.
Рішення
Відомо: Вода стабільно тече через сопло.
Знайти: Знайдіть загальну силу, що чиниться болтами на сопло, щоб утримувати її на місці.
Дано:
.jpg)
Малюнок5.2.5: Труба і сопло, присвоєні з системою координат і марковані всіма заданими величинами.
Аналіз:
Стратегія: Спробуйте лінійний імпульс уx -напрямку, оскільки проблема просить сили (механізм передачі лінійного імпульсу), а сили знаходяться вx -напрямку.
Система→ Виберіть відкриту, що не деформується систему, яка розрізає трубу на з'єднанні сопла труби і включає в себе сопло.
Властивість для підрахунку→ Спробуйте лінійний імпульс і, можливо, масу (якщо нам потрібно пов'язати вхід зі швидкістю вихідного потоку.
Період часу→ Схоже, що це може бути швидкість (нескінченно малий проміжок часу) або сталий стан завдання.
.jpg)
Малюнок5.2.6: Вибір системи для цієї проблеми.
Починаючи з системи, показаної пунктирною лінією, визначте всі передачі імпульсу для системи. Пройшовши пальцями навколо кордону системи, ви б ідентифікували шість болтових сил, сили тиску та два масові транспорти імпульсу. Тепер записуючи їх у векторному рівнянні для лінійного імпульсу вx -напрямку, ми маємо:dPx, sysdt=[6Fbolt, x+Fnet pressure, x]+[˙mV1, x−˙mV2, x]
Для отримання правильних напрямків сил тепер потрібна більш повна діаграма імпульсу. Повна схема показана нижче.
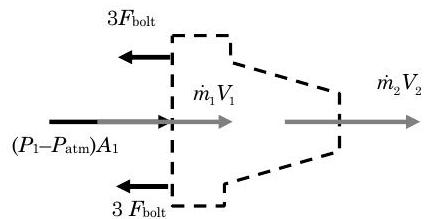.jpg)
Малюнок5.2.7: Схема вільного корпусу для системи форсунок.
Перш ніж продовжувати, ми повинні пояснити, як ми отримали різні терміни.
- Терміни масового транспорту - це добуток масової витрати та швидкості на будь-якій межі потоку. Напрямок стрілки знаходиться в напрямку швидкості.
- Дві стрілки показують зусилля затвора. Кожна стрілка являє собою три (3) болта. Крім того, можна визначити тільки середнє зусилля болта. Зверніть увагу, що так як болти знаходяться в натягу, стрілки вказують на те, що болти тягнуть по системі.
- Чисті сили тиску вx -напрямку повинні бути розраховані, враховуючи розподіл тиску по всій межі системи. Як показано на малюнку, атмосферний тискP атм діє на всі поверхні, крім площі вхідного потоку, де знаходиться тискP1. Зверніть увагу, що всі стрілки тиску вказують на поверхню. Чисту силу можна визначити, віднімаючи від атмосферного тиску, як показано на малюнку. В результаті виходить рівномірний тиск, щоPnet =P1−Patm діє над площею входу. Величина результуючої сили дорівнюєFnet pressure, x=(P1−Patm)A1. Ця стрілка вказує на поверхню і показана на діаграмі імпульсу вище.
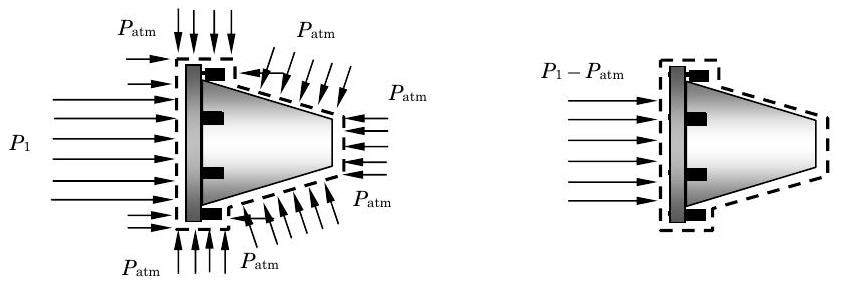
Малюнок5.2.8: Еквівалентні методи вираження чистого тиску, що відчувається системою форсунок.
Тепер все, що залишилося - вирішити за болтові сили. Запис рівняння імпульсу у вигляді скаляра дляx− напрямку, який ми маємо:
dPx, sysdt=0⏟Steady-state=[−6Fbolt, x+Fnet pressure, x⏟=(P1−Patm)A1]+[˙m1(+V1, x)−˙m2(+V2, x)]⏟+ sign for each V since a positive valuefor V1, x and V2, x represents a positivespecific linear momentum0=−6Fbolt, x+(P1−Patm)A1+[˙m1V1−˙m2V2]→6Fbolt, x=(P1−Patm)A1+[˙m1V1−˙m2V2]
Подальше спрощення може бути досягнуто шляхом застосування консервації маси до тієї ж системи з подальшим застосуванням сталого припущення:
dmsysdt=0=˙m1−˙m2→˙m2=˙m1→ρ1A1V1=ρ2A2V2⏟Incompressible liquid
Використовуючи цей результат, рівняння для зусиль болта стає6Fbolt=(P1−Patm)A1+˙m1(V1−V2)
Рішення для ділянки на вході:A1=π4D21=π4(0.25 m)2=4.909×10−2 m2
Рішення для масової витрати:˙m1=ρA1V1=(1000 kgm3)(4.909×10−2 m2)(5 ms)=245.5 kgs
Швидкість на виході стає:V2=A1A2V1=[(π/4)D 21(π/4)D 22]V1=(D1D2)2V1=(25 cm12 cm)2(5ms)=21.70 ms
Підстановка цих чисел назад в загальний результат дає6Fbolt=(P1−Patm)A1+˙m1(V1−V2)=[(500−100) kPa](4.904×10−2 m2)+(245.5 kgs)(5.00−21.70)ms=(19.64 kPa⋅m2)(1000 N/m2kPa)+(−4100kg⋅ms2)(N(kg⋅ms2))=19.64×103 N+(−4.10×103 N)=15.5 kN
Таким чином, шість болтів повинні чинити загальну силу15.5 kN дії вліво (або до труби), щоб утримувати сопло на місці.
Коментарі:
- Відзначимо, що збільшення питомого лінійного імпульсуV, тобто маси, що йде з системи, фактично служить для зниження навантаження на болти. Щоб переконатися в цьому, розглянемо, яке було б зусилля болта, якби форсунка була закрита.
- Як би змінилося рішення, якби ми вибрали базовуx координату ліворуч, а не праворуч, як показано? Векторне відношення залишилося б колишнім, але скалярне рівняння стало б таким
0=6Fbolt, x−(P1−Patm)A1+[˙m1(−V1)−˙m2(−V2)]→6Fbolt, x=(P1−Patm)A1+[˙m1(V1)−˙m2(V2)]
Канатна дорога натягується по закріпленому накладному кабелю тросом, прикріпленим в точціA. Автомобіль має масу200 kg, а натяг в тросі є2400 N. Автомобіль підтримується колесами, які спираються на трос. Кабель нахилений під кутомθ=22.6∘ з горизонталлю, як показано на малюнку.
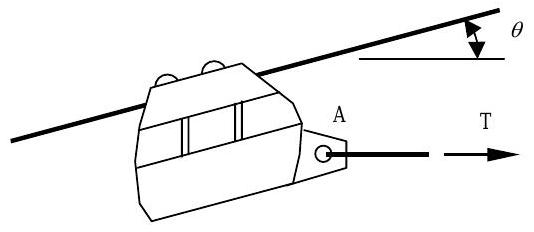
Малюнок5.2.9: Підвішена до кутового троса канатна дорога тягнеться вправо горизонтальним тросом.
Визначити:
(а) Величина і напрямок сили, щоR чиниться накладним кабелем на колеса автомобіля, в ньютонах.
(б) Величина і напрямок розгону автомобіля вm/s2.
Рішення
Відомо: Невеликий оглядовий автомобіль тягнеться уздовж нерухомого верхнього кабелю тросом, прикріпленим в точціA
Знайти: (а) Величина і напрямок сили, щоR чиниться накладним тросом на колеса автомобіля, в ньютонах. (б) Величина і напрямок прискорення автомобіля, вm/s2.
Дано:
T=2400 Nmcar=200 kgθ=22.6∘
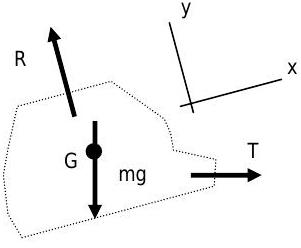.jpg)
Малюнок5.2.10: Схема вільного кузова ізольованої канатної дороги.
Аналіз:
Стратегія→ Оскільки проблема передбачає сили, спробуйте зберегти лінійний імпульс.
Система→ Закрита система включає лише автомобіль, як показано на схемі системи імпульсу праворуч.
Властивість→ Лінійний Імпульс
Час Період→ Миттєвий
Без вибору системи координат збереження лінійного рівняння імпульсу стає там,ddtPsys=∑externalFj+∑in˙miVi=0−∑out˙meVe=0, closed system→ddtPsys=msysg+T+R де є тільки три зовнішні сили - сила на колесахRmsysg, вага автомобіля і сила тросаT. Чиста сила тиску дорівнює нулю, оскільки атмосферний тиск оточує автомобіль.
Крім того, оскільки це замкнута система лінійного імпульсу системи,Psys=msysVG деVG є швидкість центру маси системи. Таким чином, збереження лінійного імпульсу тепер можна записати якddt(msys VG)=msys g+T+R→msys dVGdt=msys g+T+R Тепер вибираючи систему координат, яка вирівнюється з кабелем, збереження лінійного імпульсу можна записати в двох компонентах. Уy напрямку лінійне рівняння імпульсу стає
msys dVG, ydt=0; no motionin y-direction=−(T⋅sinθ)+R−(msys g⋅cosθ)→R=(T⋅sinθ)+(msys g⋅cosθ)
після рішення для силиR.
Підстановка в числовій інформації даєR=(2400 N)⋅sin(22.6∘)+(200 kg)(9.81 ms2)⋅cos(22.6∘)=922.3 N +1811 N=2733 N
Уx напрямку лінійне рівняння імпульсу стаєmsysdVG, xdt=(T⋅cosθ)−(msys g⋅sinθ)dVG, xdt=(T⋅cosθ)−(msys g⋅sinθ)msys=(Tmsyscosθ)−(g⋅sinθ)
Згадуючи визначення прискорення, рівнянняx -імпульсу може бути вирішено для прискорення, оскількиaG, x≡dVG, xdt=(Tmsyscosθ)−(g⋅sinθ) підстановка в числовій інформації даєaG, x=(2400 N200 kg)cos(22.6∘)−(9.81 ms2)sin(22.6∘)=(12.0 ms2)(0.9232)−(9.81 ms2)(0.3843)=7.31 ms2
Коментарі:
- В рамках дослідження безпеки визначте, як зміниться силаR і прискорення автомобіля, якщо тягне трос раптово зламався.
- Після виходу з ладу тягне троса максимальна швидкість канатної дороги обмежується механізмом екстреного гальмування в колісній каретці.15 m/s Гальмівне зусилля активується при досягненні швидкості «падаючого» автомобіля5 m/s. Яке гальмівне зусилля необхідно надати на канатну дорогу, щоб обмежити швидкість автомобіля? Якщо автомобіль нерухомий при розриві троса, що тягне, скільки часу знадобиться для активації аварійного гальма і коли буде досягнута максимальна швидкість?
Для зважування води в баку використовується шкала. Вода стабільно тече через бак, як показано на малюнку. Він надходить у верхній частині бака з об'ємною швидкістю потоку30 m3/s через трубу діаметром6 cm. Вона виходить збоку ємності через круглий отвір6−cm діаметром. Обсяг води в баку дорівнює0.6 m3, а суха вага бака -500 N. Визначте показання шкали, в ньютонах.
.png)
Малюнок5.2.11: Вода надходить в резервуар за шкалою через отвір 1 і виходить з резервуара через отвір 2.
Рішення
Відомо: Вода стабільно тече через резервуар, який спирається на шкалу.
Знайти: Зчитування шкали.
Дано:
Впускна труба @ 1
Об'ємний˙V−1=30 m3/h
діаметр витратиD1=6 cm
Відкриття на виході @ 2
ДіаметрD2=6 cm
Обсяг води в баку в сталому стані:V−water=0.6 m3
Вага бака:Wtank=500 N
Аналіз:
Стратегія→ Оскільки проблема передбачає сили, спробуйте зберегти лінійний імпульс.
Система→ Відкрита система, яка включає всю воду в резервуарі та резервуарі, як показано на схемі системи імпульсу.
Властивість для підрахунку→ Лінійний імпульс і маса Період
часу→ Миттєвий
.jpg)
Малюнок5.2.12: Вільна схема корпусу системи, що складається з бака і води в ньому.
Написання курсової форми збереження лінійного рівняння імпульсу для цієї задачі дає
dPsysdt=∑externalFj+∑in˙miVi−∑out˙meVedPsyss=0steady state=(Wtank+Wwater)+Fscale+˙m1V1−˙m2V2 A0=(Wtank+Wwater)+Fscale+˙m1V1−˙m2V2
Тепер записуючи складову цього рівняння у напрямку y, як визначено на малюнку вище,0=[Wtank+Wwater]−Fscale+˙m1V1,y−˙m2V2,y=0No y-component @ 2
Рішення дляFscale насFscale=Wtank+Wwater+˙m1V1,y
Тепер рішення для ваги танка уWtank нас єWwater=mwater g=(ρwaterVwater)g=(1000 kgm3)(0.600 m3)(9.81 ms2)=5886 N
y-складова швидкості при 1 і масової витрати при 1 є
V1,y=V1=˙V−1A1=˙V−1(π4D 21)=(30 m3h×1 h3600 s)π4(0.06 m)2=2.95 ms˙m1=ρ1˙V−1=(1000 kgm3)(30 m3h×1 h3600 s)=8.33 kgs
Поєднуючи це, щоб вирішити силу шкали на танку,Fscale:Fscale=Wtank +Wwater +˙m1V1,y=(500 N)+(5886 N)+(8.33 kgs)(2.95 ms)=(6386 N)+(24.6 N)=6411 N
Якби оператор знехтував впливом води, що стікає в бак, на показання, він би завищив кількість води в баку приблизно0.4%.
Коментар:
Яка величина і напрямок горизонтальної сили, яку шкала повинна чинити на бак, щоб він не ковзав з платформи? [Відповідь:24.6 N←] Як ви можете використовувати вимірювання бічної сили для позначення швидкості потоку?
