5.4: Лінійний імпульс, лінійний імпульс та імпульсні сили

Як ми вже продемонстрували, іноді необхідно інтегрувати форму швидкості збереження лінійного рівняння імпульсу протягом заданого часового інтервалу. Це дає залежність між зміною лінійного імпульсу всередині системи та величиною лінійного імпульсу, що транспортується в систему. Історично такі типи розрахунків були зроблені шляхом введення величини, відомої як лінійний імпульс. За певних умов система буде піддаватися відносно великій силі протягом дуже короткого часового інтервалу, наприклад, контакту між двома більярдними кулями або удару між двома автомобілями, коли вони стикаються. Ці великі, короткочасні сили відомі як імпульсивні сили, а взаємодія називається впливом. У цьому розділі ми продемонструємо, що обчислення ударів для імпульсних та імпульсних сил природно випливають з нашого розуміння основного збереження лінійного рівняння імпульсу.

5.4.1 Лінійний імпульс

Коли сила діє на межу системи, лінійний імпульс протікає через межу із заданою швидкістю - чим більша величина сили, тим більша швидкість транспортування лінійного імпульсу. Якщо розглядати просту частинку з\(\mathbf{F}\) діючою на неї єдиною силою, то відомо, що швидкість зміни лінійного імпульсу системи дорівнює\[\frac{d \mathbf{P}_{\mathrm{sys}}}{d t}=\mathbf{F} \nonumber \]

За визначенням лінійний імпульс сили\(\mathbf{F}\) є інтегралом сили по відношенню до часу:\[\mathbf{Impulse }_{t_{1} \rightarrow t_{2}} = \int\limits_{t_{1}}^{t_{2}} \mathbf{F} \ dt \nonumber \]

Як видно на малюнку\(\PageIndex{1}\), це являє собою площу під\(t\) кривою.\(\mathbf{F}\)

Малюнок\(\PageIndex{1}\):\(\mathbf{F}\) -\(t\) крива.

Для частинки ми бачимо, що імпульс сили\(\mathbf{F}\) якраз дорівнює зміні лінійного імпульсу частинки:\[\mathbf{Impulse} \left. \right|_{\mathbf{F}, \ t_{1} \rightarrow t_{2}} = \int\limits_{t_{1}}^{t_{2}} \mathbf{F} \ dt = \int\limits_{t_{1}}^{t_{2}} \left( \frac{d \mathbf{P}_{\mathrm{sys}}}{d t} \right) dt = \mathbf{P}_{\mathrm{sys}, 2}-\mathbf{P}_{\mathrm{sys}, 1} \nonumber \]

Для будь-якої системи імпульс заданої сили дорівнює величині лінійного імпульсу, перенесеного через межу системи за вказаний проміжок часу. Вона не завжди дорівнює зміні лінійного імпульсу системи. Нерідко неможливо безпосередньо виміряти величину сили в залежності від часу. В цьому випадку прийнято говорити про імпульс сили і по можливості визначати імпульс шляхом вимірювання зміни лінійного імпульсу системи.

5.4.2 Імпульсивні сили

Неможливість вимірювання деталей заданої сили як функції часу особливо актуальна під час ударів. Імпульсивна сила - це відносно велика сила, яка діє протягом дуже короткого періоду часу - наприклад, коли м'яч для боулінгу потрапляє в боулінг. Коли це відбувається, куля для боулінгу передає лінійний імпульс на штифт короткочасною контактною силою. Те ж саме було б вірно лінійного імпульсу, наданого homerun крок, як бейсбол впливає на біту slugger 's протягом дуже короткого періоду часу. За дуже малий проміжок часу можна оцінити величину середньої імпульсної сили, припустивши, що сила постійна протягом малого часового інтервалу:\[\mathbf{F}_{\text {avg }} \Delta t = \int\limits_{t}^{t+\Delta t} \mathbf{F} \ dt = \left. \mathbf{Impulse} \right|_{\mathbf{F}, \ t_{1} \rightarrow t_{2}} \quad \rightarrow \quad \mathbf{F}_{\text {avg}} = \frac{1}{\Delta t} \int\limits_{t}^{t+\Delta t} \mathbf{F} \ dt \nonumber \] Як показано на малюнку\(\PageIndex{2}\), середня імпульсна сила дорівнює постійній силі, яка діє протягом того ж часового інтервалу і передає таку ж кількість лінійного імпульсу, що і вихідна змінна в часі сила.

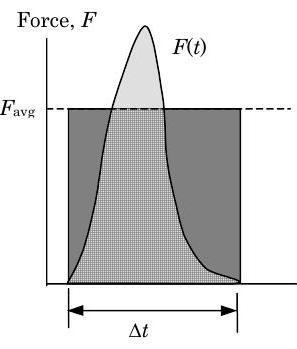
Малюнок\(\PageIndex{2}\): Імпульсивна сила.

Перевірте своє розуміння - оцінка пікової сили під час імпульсного навантаження

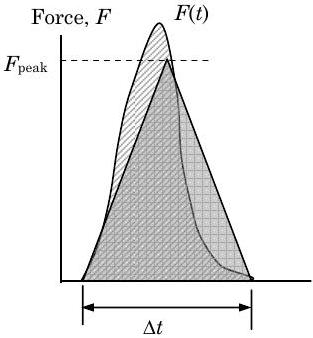
При розрахунку середньої імпульсної сили вище ми припустили, що форму і площу\(\mathbf{F}\) -\(t\) кривої найкраще можна наблизити прямокутною коробкою висоти\(F_{\text {avg}}\) і ширини\(\Delta t\). Є й інші можливі форми, які ми могли б використовувати для наближення\(\mathbf{F}\) -\(t\) кривої. Припустимо, ми наблизили площу під\(\mathbf{F}\) -\(t\) кривою за допомогою рівнобедреного трикутника висоти\(F_{\text {peak}}\) і підстави\(\Delta t\).

Який зв'язок між\(F_{\text {avg}}\) і\(F_{\text {peak}}\) для імпульсивної ситуації навантаження тривалості\(\Delta t\)? Яке значення дає кращу оцінку максимального зусилля, яке відчуває система під час удару і чому вона краще?

Малюнок\(\PageIndex{3}\): Імпульсне наближення сили за допомогою рівнобедреного трикутника.

Приклад — Зіткнення вагонів

Два коробкових вагонів повинні бути з'єднані разом у залізничному розподільному дворі. Boxcar A рухається вправо зі швидкістю\(3 \mathrm{~km} / \mathrm{h}\) і повинен бути з'єднаний з вагончиком B, який спочатку нерухомий. Вагон-вагон А має масу\(45,000 \mathrm{~kg}\) і вагон В має масу\(25,000 \mathrm{~kg}\).

Визначте (а) кінцеву швидкість з'єднаних автомобілів і (б) середню імпульсну силу, що діє на кожен автомобіль під час зчеплення, якщо процес зчеплення приймає\(0.3 \ \text{s}\).

Рішення

Відомо: Два вагони стикаються і з'єднуються між собою.

Знайти: (а) кінцева швидкість спарених автомобілів

(б) середня імпульсна сила на автомобілі, якщо процес зчеплення займає\(0.3 \ \text{s}\).

Дано:

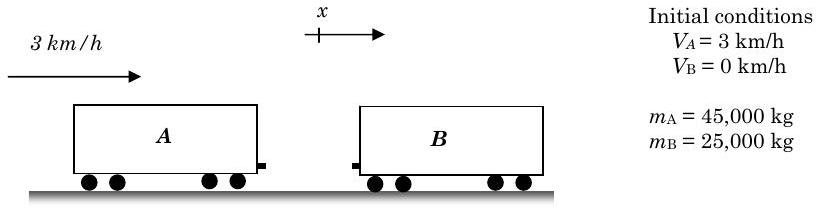
Малюнок\(\PageIndex{4}\): Початкові умови і відносні положення двох коробкихвагонів.

Аналіз:

Стратегія\(\rightarrow\) Оскільки ця проблема включає два об'єкти, що стикаються з ударом, спробуйте подивитися на збереження лінійного імпульсу.

Система\(\rightarrow\) я поки не впевнений, вирішу це через хвилину.

Властивість підрахунку\(\rightarrow\) Лінійний імпульс у\(x\) напрямку -direction.

Часовий інтервал\(\rightarrow\) Кінцевий час, так як зацікавлені в поведінці до і після.

Тепер розглянемо, яку систему підібрати. Спробуємо використовувати рухому закриту систему, яка включає в себе тільки коробкові вагони.

Малюнок\(\PageIndex{5}\): Вибір системи, до і після зіткнення.

Зверніть увагу, що якщо ми розглядаємо лише\(x\) -імпульс, немає сил, що діють на систему з компонентом у\(x\) напрямку -direction. Таким чином, збереження лінійного рівняння імпульсу стає\[\frac{d P_{x, \ \text{sys}}}{dt} = \sum \underbrace{F_{x \ \text {external}}}_{\text {No } x \text{-forces}} + \underbrace{ \sum_{i} \cancel{ \dot{m} V_{x, i} }^{=0} - \sum_{e} \cancel{ \dot{m} V_{x, e} }^{=0} }_{\text {Closed System}} \rightarrow P_{x, \ \text{sys}} = \text {constant} \nonumber \]

Використання цього результату для зв'язку лінійного імпульсу системи до і після удару дає наступне:\[\begin{gathered} &P_{x, \ 1} = m_{A} V_{A, \ 1} + m_{B} \cancel{V_{B, \ 1}}^{=0} \\ &P_{x, 2} = m_{A} \cancel{ V_{A, \ 2} }^{=V_{2}} +m_{B} \cancel{ V_{B, 2} }^{=V_{2}} \end{gathered} \rightarrow \quad \rightarrow \quad \begin{gathered} P_{x, \ 1} = P_{x, \ 2} \\ m_A V_{A, \ 1} = \left( m_{A}+m_{B} \right) V_{2} \end{gathered} \quad \rightarrow \quad V_{2} = \frac{m_{A}}{\left(m_{A} + m_{B}\right)} V_{A, \ 1} \nonumber \]

Вирішення для кінцевої швидкості у нас є\(V_{2} = \dfrac{m_{A}}{\left(m_{A}+m_{B}\right)} V_{A, \ 1} = \dfrac{45}{(45+25)}\left(3 \ \dfrac{\mathrm{km}}{\mathrm{h}}\right) = 1.93 \mathrm{~km} / \mathrm{h}\).

А оскільки це позитивне число, то спарені поїзди продовжать рух вправо (позитивне\(x\) -напрямок). Це відповідь на Частина (а).

Тепер, щоб визначити середню імпульсну силу, ми повинні помістити межу, де виникає сила. Розглянемо замкнуту систему, яка включає в себе тільки вагон Б. Починаючи зі збереження лінійного імпульсу для цієї замкнутої системи дає\( \dfrac{d P_{x, \ \text{sys}}}{d t} = F_{\text {coupling}} \).

Малюнок\(\PageIndex{6}\): Закрита система, що складається з Boxcar B

Але щоб знайти середню силу зчеплення на автомобілі B, ми повинні інтегрувати цей вираз протягом часового інтервалу:\[\int\limits_{t_{1}}^{t_{2}} \left( \frac{d P_{x, \ \text{sys}}}{d t} \right) dt = \int\limits_{t_{1}}^{t_{2}} F_{\text {coupling }} dt \quad \rightarrow \quad P_{x, \ 2} - P_{x, \ 1} = F_{\text {coupling, avg }} \Delta t \nonumber \] Вирішення для сили, яку ми маємо\[\begin{aligned} F_{\text {coupling, avg}} &= \frac{P_{x, \ 2}-P_{x, \ 1}}{\Delta t} = m_{B} \frac{V_{B, \ 2}-V_{B, \ 1}}{\Delta t} \\[4pt] &=(25,000 \mathrm{~kg}) \left[ \frac{(1.93-0) \ \dfrac{\mathrm{m}}{\mathrm{h}}}{(0.3 \mathrm{~s})} \right] \left( \frac{\mathrm{h}}{3600 \mathrm{~s}} \right) \left( \frac{\mathrm{N} \cdot \mathrm{s}^{2}}{\mathrm{kg} \cdot \mathrm{m}} \right) = 44.7 \times 10^{3} \mathrm{~N} = 44.7 \ \mathrm{kN} \end{aligned} \nonumber \]

Оскільки значення позитивне, то напрямок сили зчеплення на автомобілі В такий, як показано на малюнку. Зчеплення зусилля, що діє на автомобіль А, має однакову величину і протилежний напрямок.

Коментар

(1) Розглянемо альтернативну систему для вирішення частини (а). Цього разу припускають відкриту систему, яка спочатку включає автомобіль B і, нарешті, включає обидва автомобілі.

Починаючи з лінійного рівняння імпульсу:\[ \frac{d P_{x, \ \text{sys}}}{dt} = \underbrace{ \sum \cancel{ F_x }^{=0} }_{\text{No forces in } x \text{-direction} } + \,\,\,\, \dot{m}_i V_{x, \ i} \,\,\,\, - \underbrace{ \cancel{ \dot{m}_e V_e }^{=0} }_{\text{No flow out of system}} \quad\quad \rightarrow \quad\quad \frac{ d P_{x, \ \text{sys}} }{dt} = \underbrace{ \dot{m}_i V_{x, \ i} }_{\begin{array}{c} x \text{-momentum carried} \\ \text{in with boxcar A} \end{array} } \nonumber \]

Щоб знайти швидкість (або лінійний імпульс) системи після зчеплення, ми повинні інтегрувати це рівняння протягом часового інтервалу:\[ \int\limits_{t_1}^{t_2} \left( \frac{d P_{x, \ \text{sys}}}{dt} \right) dt = \underbrace{ \int\limits_{t_1}^{t_2} \left( \dot{m}_i V_i \right) dt }_{\begin{array}{c} = \text{ all of the momentum} \\ \text{carried into the system} \\ \text{by boxcar A} \end{array}} \quad \rightarrow \quad \underbrace{ P_{x, \ 2} }_{\begin{array}{c} \text{Includes} \\ \text{both cars} \end{array}} - \underbrace{ P_{x, \ 1} }_{\begin{array}{c} \text{Only} \\ \text{car B} \end{array}} = m_A V_A \quad\quad \rightarrow \quad\quad \left( m_A + m_B \right) V_2 = m_A V_A \nonumber \]

Рішення продовжується з цього моменту, як зазначено вище. Зверніть увагу, як починаючи з іншої системи, навіть відкритої системи, ми можемо відновити одне і те ж рівняння, використовуючи послідовні припущення. Це ілюструє, що часто можна вирішити одну і ту ж проблему за допомогою декількох різних систем.

(2) Виберіть відкриту систему, яка має масу, що надходить і виходить під час удару, і вирішити кінцеву швидкість з'єднаних автомобілів. [Підказка: Ця система не матиме лінійного імпульсу ні в початковому, ні в кінцевому станах.]

(3) Скільки часу знадобилося б спареним автомобілям, щоб прийти до повної зупинки, якщо гальма на автомобілі B були заблоковані в момент удару і коефіцієнт кінетичного тертя між колесами і рейкою\(0.10\)? Якою буде швидкість спарених автомобілів відразу після удару? Чи було б розумно знехтувати силою тертя під час удару? [Відповідь:\(1.53\) секунди].