7: Прискорена продуктивність - Зліт і посадка
Глава 7. Прискорена продуктивність: зліт і посадка
Вступ
До цього моменту вся наша дискусія стосувалася статичного або неприскореного польоту, де F = ma = 0. Навіть при підйомі і спуску ми припускали «квазірівневі» умови, коли сили на літаку підводилися до нуля. Якщо ми хочемо подивитися на продуктивність літака під час зльоту і посадки, ми повинні, в перший раз, розглянути прискорення (під час зльоту) і уповільнення (під час посадки). Ми також матимемо пару нових сил, які слід враховувати в грунті сили реакції та тертя землі.
У зльоті літак розганяється з нульової наземноїшвидкості (але не обов'язково нульової швидкості польоту!) до швидкості, з якою він може підніматися з землі. Тяга повинна перевищувати опору, щоб відбувся прискорення, і підйомник не дорівнюватиме вазі до моменту підйому. Літак може розганятися вздовж землі під заданим кутом атаки (або коефіцієнтом підйому) до тих пір, поки швидкість не досягне точки, де динамічний тиск поєднується з коефіцієнтом підйому, щоб дати підйом рівний вазі, або він може прискорюватися під деяким кутом атаки, визначеним висотою його шасі до моменту його досягає швидкості, яка дасть підйом дорівнює вазі, коли літак потім повертається (хвостом вниз, носом вгору) до більш високого кута атаки і коефіцієнта підйому.
Будь-який пілот скаже вам, що зліт і посадка - це те, що таке політ. Трепет повного дроселя і максимального прискорення, коли літак реве вниз по злітно-посадковій смузі, а потім звільнення душі, яка виходить від обману тяжкості і розриву зв'язку з землею незрівнянна. Звичайно, пілот сподівається, що це станеться до того, як буде досягнуто кінець злітно-посадкової смуги і таким чином, щоб дозволити очищення водонапірної вежі в кінці смуги!
При посадці слід забезпечити уповільнення за допомогою гальмування, аеродинамічного опору, тертя землі та, можливо, зворотної тяги, щоб уповільнити площину до нульової швидкості; сподіваємось, до того, як він досягне кінця злітно-посадкової смуги!
Посадка є кінцевим викликом людини проти природи, оскільки пілот знову намагається залишатися під контролем запланованої зустрічі з землею в транспортному засобі, що рухається зі швидкістю, що може призвести до миттєвого каліцтва і смерті, якщо є найменший прорахунок поперечного вітру або вниз тяги. Звичайно, все це повинно бути зроблено таким чином, щоб запевнити пасажира, що кожен крок є безпечним і природним і контролюється, як неділю вдень їзди на поле для гольфу.
Вітер буде фактором зльоту та посадки, і можна подумати, що було б очевидно, що пілот повинен розташувати літак в кінці злітно-посадкової смуги, що призведе до роботи на вітер. Це призведе до зменшення довжини ґрунтового рулону під час зльоту або посадки. Для деяких, однак, це може бути не очевидним.
Автор одного разу сидів у аспірантурі студента транспортного машинобудування, який пройшов кілька курсів з проектування аеропортів. На питання, яку роль відігравали переважаючі вітри в оформленні аеропортів, студент виявився спантеличеним. З огляду на натяк, що це має щось спільне з тим, як вирівнювалися злітно-посадкові смуги, він все одно намалював порожній. Нарешті, коли його попросили намалювати злітно-посадкову смугу і показати літак, який готується до зльоту на одному кінці і пояснити, яким чином вітер дме, очі учня засвітилися в явному одкровенні істини. Він намалював злітно-посадкову смугу горизонтально по центру дошки з літаком на правому кінці, готовий розпочати злітно-посадкову смугу ліворуч. Потім він тріумфально намалював стрілку, щоб позначити вітер, що рухається справа наліво, в тому ж напрямку, що і рух літака!
Коли відчай і похмурість оселилися над факультетом у кімнаті, я, досить неохоче, запитав його, чому літак злетить в тому ж напрямку, як дув вітер. Він відповів, що відповідь очевидна: «Тож вітер перенесе забруднення з літаком!» Слідкуйте за екологами, які проектують аеропорти!
Для вивчення продуктивності літаків при зльоті і посадці ми повинні переконатися, що ми маємо належні визначення того, що ці фази польоту тягнуть за собою. Потім треба розглянути сили, що діють на літак. Ми почнемо це дослідження з розгляду зльоту.
7.1 Продуктивність зльоту
Визначення, яке використовує Федеральне управління авіації для зльоту, включає наземний хід від нульової швидкості на землі до точки, де колеса залишають землю, плюс відстань, необхідну для очищення 50-футової перешкоди. Відстань над землею для всього перерахованого вище обчислюється при максимальній вазі брутто в стандартних умовах рівня моря. Стан «найгіршого випадку» часто також розраховується на спекотний день на великій висоті (100ºF у Денвері).
Ми будемо стосуватися лише наземної частини зльоту, знаючи, що ми можемо знайти відстань, щоб очистити 50-футову перешкоду від наших рівнянь підйому. Цей підйом буде розрахований на максимальний кут підйому умов.
Першим кроком розрахунку наземного пробігу, необхідного для зльоту, є експертиза сил на літаку. На додаток до підйому, опору, тяги та ваги, тепер ми повинні враховувати тертя землі та «результуючу» силу землі в підтримці всієї або частини ваги літака. Вони показані на малюнку нижче. Коефіцієнт тертя буде залежати від поверхні грунту і гальмівного тертя.
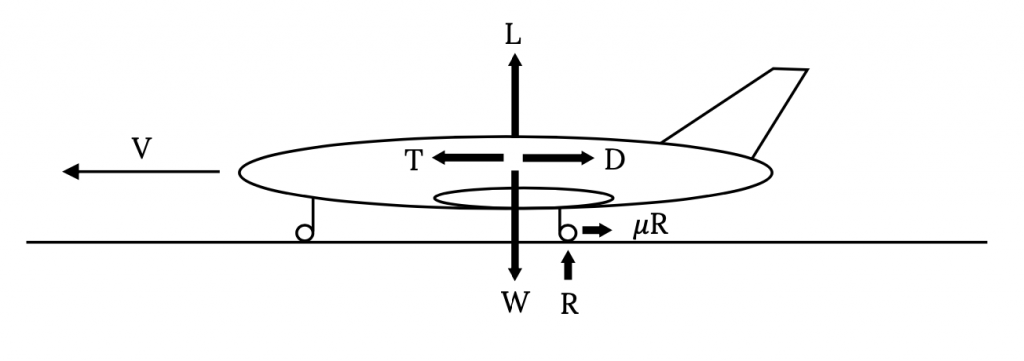
Підсумовування вертикальних сил на малюнку 7.1 дає
Л + Р ‑ Ш = 0
або
R = Ш ‑ Л
Підсумовування горизонтальних сил дає
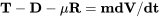
Зверніть увагу, що у вищезгаданому співвідношенні ми вперше маємо прискорення. Ці сили змінюються, коли літак розганяється від спокою до швидкості зльоту.
Поєднуючи два рівняння вище, ми маємо одне відношення.
![T−d−μ (Ш−Л) = [Вт/г] [дВ/дТ]](https://eng.libretexts.org/@api/deki/files/49365/a973d5829affa91cc49ca82fb67560e0.png)
які можна переставити, щоб дати
![g [(T/W) −μ] − (г/Вт) [Д−мкл] = дВ/дт](https://eng.libretexts.org/@api/deki/files/49366/4d588b0c5c6777c0c5765301bd6f6a08.png)
Наше бажання полягає в тому, щоб інтегрувати це або пов'язане з ним рівняння, щоб отримати час і відстань, необхідні для зльоту. Для цього ми повинні спочатку врахувати залежність як підйому, так і опору від швидкості. Це дає
де C Lg позначає коефіцієнт підйому під час зльоту або посадки наземного пробігу, а не те, що в польоті або в точці зльоту або приземлення самого.
Вищевказане рівняння все ще містить тягу і вагу, обидва з яких цілком можуть змінюватися під час зльоту грунту. Тяга, як відомо, є функцією швидкості, однак вага буде залежати від швидкості використання палива (питомої витрати палива) і буде залежати від часу, а не швидкості. Для того, щоб наш аналіз був відносно простим, ми вважатимемо зміну ваги під час зльоту незначною і розглядати вагу як константу в рівнянні. Ми будемо використовувати модель тяги, яку ми вивели з рівняння імпульсу в главі 2,
Т = Т 0 -АВ 2
У цьому рівнянні T 0 - тяга з нульовою швидкістю або «статична тяга», а - постійна (яка могла бути нульовою) і T - тяга з будь-якою швидкістю. Заміна цієї моделі на тягу в наше рівняння прискорення дає:
Слід зазначити, що швидкість в цьому рівнянні - це повітряна швидкість, а не швидкість щодо землі. Коли ми дивимось на відстань зльоту, нам доведеться турбуватися як про наземну швидкість, так і швидкість польоту. Найпростішим буде випадок, коли немає наземного вітру; тобто коли швидкість польоту і швидкість землі рівні.
У наведеному вище співвідношенні всі терміни в дужках і дужках є по суті постійними для даного літака на заданій висоті злітно-посадкової смуги та для заданої поверхні злітно-посадкової смуги. Коефіцієнту підйому дається спеціальне позначення ClG, щоб позначити, що це значення тільки для наземного прогону. У звичайному злітному крені літак прискорюється до заздалегідь визначеної швидкості, а потім «обертається» до більш високого кута атаки, що дасть достатній підйом, щоб призвести до зльоту на такій швидкості. Отже, коефіцієнт підйому наземного ходу, ймовірно, не буде таким же, як коефіцієнт підйому зльоту. Коефіцієнт опору може бути аналогічно індексований; однак, оскільки CD є функцією CL і згодом буде записаний таким чином, цього не буде зроблено на цьому етапі.
Оскільки більшість членів у рівнянні можна розглядати як константи, рівняння можна спростити наступним чином:
дВ /дТ = А — БВ 2,
де
і
Ця залежність прискорення може бути інтегрована для отримання часу для наземного ходу зльоту.
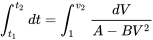
Припускаючи, що літак починає злітну бігу з відпочинку і що немає наземного вітру і що верхня межа - швидкість зльоту V ДО, ми маємо
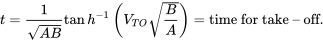
ПРИМІТКА: Це може бути перший раз, коли читач коли-небудь бачив зворотний гіперболічний тангенс. Що повинно слідувати це шалений пошук вашого калькулятора, щоб побачити, чи є така клавіша або комбінація клавіш поряд з однаково поспішною перевіркою індексів середньої школи та коледжу триг і обчислення текстів, щоб побачити, що, чорт візьми, ця річ. Очікування, щоб зрозуміти це під час тесту, може призвести до значного збентеження.
Питання, яке слід враховувати тут: «Яке хороше значення для швидкості зльоту?»
Найнижча швидкість, з якою літак може піднятися з землі, - це швидкість стійла для прямого та рівного польоту на висоті злітно-посадкової смуги. Однак не безпечно намагатися зльоту на цій мінімальній швидкості літаком прямо на межі стійла. Трохи вище, ніж стійла швидкість дасть запас міцності, який дозволить злітати на досить низькій швидкості без ризику затримки через несподівані пориви або подібні проблеми. Загальновикористовувані значення для зльоту швидкості діапазону від 10 до 20 відсотків вище, ніж пряма і рівень швидкості затримки.
1.1 В стійло < V ДО < 1.2 В стійло.
Будемо вважати більш високе значення,
V ДО = 1,2 В стійло,
якщо не сказано інше.
Набагато важливішим, ніж час, необхідний для зльоту наземного пробігу, є відстань, необхідну. Завжди приємно знати, що пілот може отримати літак в повітря, перш ніж він досягне кінця злітно-посадкової смуги! Щоб знайти відстань зльоту, ми повинні інтегрувати відстань, а не час.
дВ/дС = (дВ /дТ) /дС/дт) = (А — БВ 2) /В
Перевпорядкування цього дає
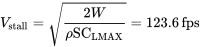
який інтегрований, щоб отримати
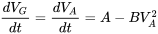
Нарешті
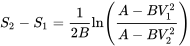
Тепер, припускаючи, що літак починається з відпочинку, ніякого вітру і підняття на ВТО у нас є
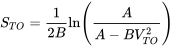
Пізніше ми розслідуємо випадок зльоту на вітрі.
Перш ніж йти далі з аналітичним аналізом розбігу злітної землі, варто зробити паузу і вивчити фізичні аспекти проблеми. Вони занадто часто втрачаються в рівняннях, особливо коли ми приховали багато термінів за зручними термінами, такими як A і B. Давайте спочатку напишемо останнє рівняння для відстані зльоту в повній красі.
З наведеного вище рівняння видно, що багато факторів впливають на відстань зльоту.
Наприклад, інтуїтивно зрозуміло, що тертя ґрунту затримує зліт. Уповільнююча сила через тертя зменшуватиметься, коли підйомник збільшується під час зльоту. Отже, здається, що нам може бути перевага рухатися вниз по злітно-посадковій смузі під високим кутом атаки таким чином, що генерується високий підйом, що призведе до зменшення сили тертя та посилить прискорення літака до швидкості зльоту. З іншого боку, високий кут атаки також дасть високий коефіцієнт опору, що затримує прискорення. У певний момент зльоту сила опору перевищить силу тертя. Чи означає це, що пілот повинен почати зліт під високим кутом атаки, а потім опустити його, щоб зменшити опір, щоб утримувати деяке співвідношення тертя та перетягування на оптимальному значенні?
А як щодо значення коефіцієнта тертя? Чи використовуємо ми один тип наземного прогону на бетонній злітно-посадковій смузі, а інший - на трав'яній смузі? А як щодо м'якої бруду? Типовими значеннями коефіцієнта тертя є:
Таблиця 7.1: Типові значення коефіцієнтів тертя
| Бетон, асфальт | 0,02 - 0,05 |
| Жорсткий газон | 0,04 - 0,05 |
| Нормальний газон, коротка трава | 0,05 |
| Нормальний газон, довга трава | 0,07 - 0,10 |
| М'який грунт | 0,10 - 0,30 |
Ймовірно, слід використовувати нижчі з перерахованих вище значень для певної поверхні, якщо не вказано робити інше.
Для зльоту «м'якого поля», наприклад, на довгій траві або м'якій землі, пілотів навчають робити кілька речей, щоб зменшити роль тертя землі на злітному валку. Зазвичай для збільшення коефіцієнта підйому рекомендується використовувати заслінки, і якщо літак має триколісний тип шасі (носове колесо та два основні колеса), пілота вчать тримати ніс вгору, що одночасно зменшить тертя на цьому колесі і дасть більший кут атаки та коефіцієнт підйому. Однією з причин популярності стилю літаків «хвостовий драггер» в перші дні авіації стало його природне перевагу в м'яких польових зльотах, які були поширені на аеродромах дня.
7.2 Мінімальний зліт наземного прогону:
При звичайному зльоті, як уже згадувалося раніше, літак розганяється вздовж злітно-посадкової смуги під досить постійним кутом атаки до досягнення бажаної швидкості зльоту. Потім площину повертають, щоб надати збільшений кут атаки та коефіцієнт підйому таким чином, щоб підйом дорівнював або перевищував вагу, дозволяючи ліфт-офф. Кут атаки при цьому грунтовому крені і, отже, коефіцієнти підйому і опору, багато в чому визначається відносними довжинами шасі і кутом, під яким крило кріпиться до фюзеляжу.
На розміри і розміщення шасі впливає безліч факторів. Приємно, якщо зубчасті стійки досить довгі, щоб пропелер не потрапив на злітно-посадкову смугу (це може бути справжньою проблемою з хвостовим кріпленням опори), а також добре, якщо центр ваги літака знаходиться між головною та допоміжною передачею. Головна передача повинна бути близько до CG, щоб забезпечити легкість обертання, але досить далеко, щоб запобігти ненавмисному обертанню. Також виникає питання про те, де зберігаються шестерні в висувній системі.
Кут розміщення крила на фюзеляжі в першу чергу буде залежати від оптимальних міркувань круїзу, таким чином, що такі речі, як опір фюзеляжу, мінімізуються, а видимість пілота є задовільною, коли крило знаходиться в кращому поєднанні коефіцієнта підйому та опору для круїзу, як визначено за допомогою співвідношення попередні глави. Також приємно, якщо в умовах круїзу прохід в комерційному літаку відносно рівний.
Важливим завданням для конструктора є пошук кута атаки крила, який дозволить мінімізувати злітно-посадковий пробіг, а потім спроектувати шасі таким чином, щоб в нормальних умовах літак сідав на свою передачу з крилом під таким кутом. Спробуємо знайти той кут або, точніше, коефіцієнти підйому і перетягування під таким кутом атаки.
Спочатку повернемося до рівняння для прискорення в грунтовому прогоні.
![ДВДТ = г (Т0В−μ) −ГВ12ρ с (CD−мкГЛ) +а] V2 ДВДТ = г (Т0В−μ) −ГВ12ρ с (CD−мкГЛ) +а] V2](https://eng.libretexts.org/@api/deki/files/49378/4ec8df9107c7ece11bb86a29e83f5666.png)
Наше бажання - максимізувати це прискорення в усі часи під час бігу. Припускаючи, що єдиною змінною у нас є кут атаки, тобто C L і C D, припускаючи, що у нас параболічний опір полярний, і далі припускаючи, що швидкість зльоту V TO не залежить від C Lg, ми можемо знайти максимальне прискорення, взявши похідну щодо C Lg і прирівнювання результату до нуля. Припущення, що V TO не залежить від C Lg, означає, що літак буде обертатися на V TO для досягнення підйому, а не дозволяється продовжувати прискорюватися, поки ліфт не відбудеться на C Lg.
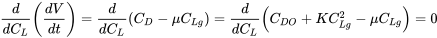
або
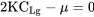
Це дає найкраще значення коефіцієнта підйому наземного прогону для мінімальної довжини траси.
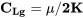
7.2.1 Примітка щодо дизайну літака
Це говорить нам про те, що якщо ми хочемо злетіти на максимально короткій відстані наземного пробігу, ми спроектуємо літак так, щоб при нормальному розподілі навантаження на злітно-посадкову смугу його крило буде під кутом атаки, що дасть вищевказане значення коефіцієнта підйому. Ми можемо зробити це, зробивши колісні стійки або опори потрібної довжини. Іншими словами, добре спроектований літак матиме своє крило, прикріплене до фюзеляжу під кутом, щоб фюзеляж був рівним в умовах круїзу і матиме висоту шасі, встановлену, щоб поставити крило під оптимальним кутом зльоту атаки при максимальних умовах валової ваги при сидінні на землі.
Це може бути цікаво побачити, наскільки велика різниця, що має оптимальний коефіцієнт підйому наземного пробігу робить, знайшовши найкращий C Lg для зльоту, а потім обчислюючи отриману відстань зльоту, а також відстань на дещо вищих і нижчих значеннях C L.
7.2.2 Потужність на основі продуктивності двигуна
Фактор, який раніше не відзначався в цій дискусії, полягає в тому, що ми врахували вихід силової установки літака з точки зору тяги, а не потужності. Це було природно, тому що ми мали справу з рівняннями сили. Що ми робимо, коли у нас є літак, який має силову силову систему (гвинт)? Ми знаємо, що тяга дорівнює потужності, розділеної на швидкість, але як ми використовуємо це в рівняннях? Можливо, приклад дасть відповідь:
ПРИКЛАД 7.1
Для літака з наступними властивостями знайдіть мінімальну дистанцію пробігу на рівні моря стандартних умов.
Ш = 56,000 фунтів
V ДО = 1,15 В стійло
η р = 0,75
S = 1000 кв. футів
С Д = 0,024 + 0,04С Л 2
Т О = 13000 фунтів
C Lmax = 2,2
μ = 0,025
Р с = 4800 к.с.
Давайте спочатку знайдемо швидкість стійла, а потім швидкість зльоту.
![Всталл = [(2 Вт)/(ρSCL)] 1/2 = 146 кадрів в секунду](https://eng.libretexts.org/@api/deki/files/49382/34074ef2f315ffc8c776e072daa33f67.png)
V TO = 1,15 В стійло = 168 кадрів в секунду.
Тепер ми повинні зіткнутися з проблемою наявності інформації про потужність та рівнянь, які вимагають даних тяги. Нам дали статичну тягу, і ми можемо припустити, що наявна потужність, яка була надана, буде потужністю, яка використовується в момент зльоту. Потім ми повинні визначити, як змінюється тяга і як пристосувати її до нашого передбачуваного співвідношення тяги проти швидкості, яке використовується в рівнянні прискорення зльоту.
На злітній швидкості
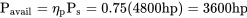
Отже, тяга при зльоті є
Т К = Р ав/В ДО = 3600 к.с./168 кадрів в секунду = (1980000 фут-фунт/сек)/168 кадрів в секунду = 11786 фунтів
Наше співвідношення тяги проти швидкості
Т = Т 0 -аВ 2.
Підставивши швидкість зльоту і тягу і статичну тягу, ми можемо знайти значення для a.
11786 фунтів = 13000 фунтів - a (168 кадрів в секунду) 2
a = 0,0430 фунтів/сек 2 /фут 2
Тоді наше відношення тяги, яке буде використано у рівняннях зльоту
Т = 1300 - 0,0430 В 2.
Тепер потрібно визначити коефіцієнт підйому при мінімальному прогоні грунту.
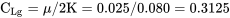
Коефіцієнт опору при мінімальному коефіцієнті підйому грунту становить:
С Д = С Д0 + КС Л 2 = 0,024 + 0,04 (0,3125) 2 = 0,0279
Нарешті, ми можемо використати все вищесказане для визначення зльоту грунту.
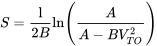
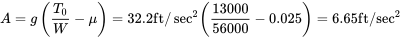
![B = ГВт [12ρ с (CD−мкГл) +а] = 3,80 × 10−5фут-1 B = ГВт [12ρ с (CD−мкГл) +а] = 3,80 × 10−5фут-1](https://eng.libretexts.org/@api/deki/files/49387/dd5b8a7d5224717b1421c37d86270d57.png)
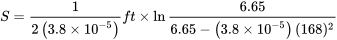
S = 2314 футів.
7.3 Зліт без обертання
Як описано раніше, звичайний зліт буде здійснюватися під кутом атаки, продиктованим конфігурацією літака та геометрією шасі, всі з яких, ймовірно, були розроблені таким чином, щоб забезпечити майже оптимальне прискорення наземного ходу. Коли досягається задана швидкість зльоту, пілот піднімає ніс літака, щоб збільшити кут атаки і дати підйом, необхідний для підйому. Але, що буде, якби замість обертання літаку дозволили просто продовжувати прискорюватися, поки він не набере достатню швидкість, щоб піднятися без обертання?
Постійне прискорення наземного ходу до зльоту без обертання не є оптимальним способом досягнення польоту. Завжди потрібно більше злітно-посадкової смуги, ніж звичайний зліт. Є, однак, обмежена кількість літаків, які призначені для цього типу ліфт-офф. Одним з відомих прикладів є бомбардувальник B-52. Цей літак має те, що може бути описано як шасі типу «велосипед» із шестернею, розташованою повністю у довгому фюзеляжі і розміщеною добре переднім і кормовим центром ваги. Таке розміщення і довгий низький фюзеляж роблять обертання практично неможливим. Результатом є необхідність дуже довгих злітно-посадкових смуг і дуже довгих, неглибоких підходів до посадки.
Оптимізація злітного пробігу для літака типу B-52 відрізняється від максимального прискорення, оптимального для звичайного зльоту. Оскільки літак не може обертатися, конструкція шестерні та розміщення крила на фюзеляжі повинні бути організовані таким чином, щоб кут атаки крила був бажаним для безпечного та ефективного підйому. Занадто високий кут атаки може призвести до зльоту в умовах занадто близько стійла, а занадто низький кут може зажадати занадто багато злітно-посадкової смуги. У наступному прикладі ми розглянемо такий літак, де конструкція така, що кут атаки крила землі встановлений таким чином, щоб дати зліт зі швидкістю на 20% вище швидкості стійла.
ПРИКЛАД 7.2
Літак, визначений нижче, призначений для зльоту без обертання, таким чином, кут атаки наземного ходу (і, отже, CL і CD) такий же, як і при зльоті. Знайти відстань зльоту в стандартних умовах рівня моря.
Ш = 75,000 фунтів
С Д = 0,02 + 0,05С Л 2
μ = 0,02
S = 2500 кв. футів
C Lmax = 1,5
Т = Т 0 = 12,000 фунтів
V ДО = 1,2 В СТІЙЛО
Спочатку ми повинні знайти швидкість стійла, швидкість зльоту та відповідний коефіцієнт підйому зльоту (і, таким чином, наземного пробігу).
![Сталл = [(2 Вт)/(ρSCL макс)] 1/2 = 129,7 кадрів в секунду](https://eng.libretexts.org/@api/deki/files/49389/782baa399a4956f726b74de76657953e.png)
V TO = 1,2 В стійло = 155,7 кадрів в секунду.
Потім ми можемо знайти коефіцієнт підйому для цієї швидкості зльоту.
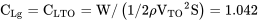
Насправді ми могли б пропустити деякі з перерахованих вище, оскільки ми зрозуміли наступне. :
C Лг = С ЛТО = [V стійла/В ДО] 2 C Lmax = [1/1,2] 2 (1,5) = 1.042
За допомогою наведеного вище коефіцієнта підйому знаходимо коефіцієнт опору.
С Д = С Д0 + КС Л 2 = 0,02 + 0,05 (1,042) 2 = 0,0742
Тепер ми готові знайти відстань зльоту.
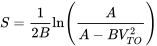
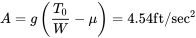
![B = ГВт [12ρ с (CD−мкГл) +а] = 6,85 × 10−5фут-1 B = ГВт [12ρ с (CD−мкГл) +а] = 6,85 × 10−5фут-1](https://eng.libretexts.org/@api/deki/files/49393/614672409199cd49b5801e08e421f093.png)
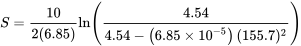
S = 3324 футів.
7.4 Тяга Розширений зліт
Хоча сьогодні це не часто зустрічається, техніка, яка колись регулярно використовувалася військовими вантажними літаками та бомбардувальниками, такими як B‑52 для зменшення дальності зльоту, включала збільшення тяги наземного ходу за рахунок використання ремінних або вбудованих твердих ракет. Цю систему часто називають JATO для реактивного зльоту, хоча вона використовувала ракети, а не струмені. Розрахунок ґрунтових прогонів для цього типу зльоту вимагає розбиття інтегральної відстані ґрунту на дві частини для обліку двох різних рівнів тяги, що використовуються в пробігу. Отримане рівняння виглядає наступним чином:
![сто=12млрд [АА−Б (ВТО2) 2] +12млрд [А1−Б (ВТО2) 2А1−БВТО2] сто=12млрд [АА−Б (ВТО2) 2] +12млрд [А1−Б (ВТО2) 2А1−БВТО2]](https://eng.libretexts.org/@api/deki/files/49395/dc1433e03f724dc0a53e241076bba3d2.png)
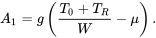
Повернемося до останнього прикладу і подивимося, що станеться, якщо ми спробуємо скоротити наземний пробіг цього літака, використовуючи 15 000 фунтів додаткової тяги, отриманої від одиниць JATO, які звільняються протягом перших десяти секунд наземного пробігу, щоб збільшити початкове прискорення літака.
Загальна тяга протягом перших десяти секунд наземного пробігу складе 27 000 фунтів. Таким чином, для цієї частини пробігу термін A у рівнянні відстані наземного пробігу буде
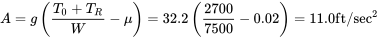
Термін B не буде змінений.
Тепер ми повинні визначити швидкість літака в кінці цього перших десяти секунд прискорення, оскільки межі рівняння відстані - це швидкості. Щоб знайти це, ми переходимо до співвідношення часу зльоту землі.
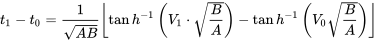
Оскільки початкова швидкість дорівнює нулю, а t 1 — t 2 = 10 сек, ми маємо
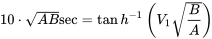
Рішення дає швидкість в кінці розширеної частини тяги злітного пробігу.
V 1 = 107 кадрів в секунду.
На даний момент не завадило б перевірити одиниці в рівняннях вище і переконатися, що ми дійсно в кінцевому підсумку з одиниць футів в секунду.
Усю відстань для зльоту тепер можна знайти наступним чином:
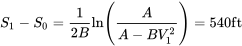
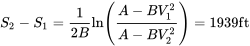
S ВСЬОГО = 2480 футів.
Прискорення JATO в цьому прикладі дало 25% зменшення наземного ходу, необхідного для зльоту. Це може бути важливо для такого літака, якщо він працює на коротких віддалених аеродромах, часто зустрічаються в країнах «третього світу» або в військових операціях.
7.5 Ефекти наземного вітру
Раніше ми згадували про важливість наземного вітру при зльоті літаків. Рідко буває, що наземного вітру не існує, отже, наші рівняння «без вітру» є, сподіваємось, найгіршим прогнозом, оскільки зліт на вітер зменшить відстань для наземного пробігу. Пошук відстані, необхідної для зльоту в наземний вітер (припускаючи, що пілот має хороший сенс літати на вітер і не намагатися «вниз вітер» зліт) вимагає іншого погляду на рівняння. Примітка. Іноді трапляються такі умови, як злітно-посадкові смуги «під гору» або перешкоди в кінці злітно-посадкової смуги, які іноді можуть спричинити необхідність зльоту під вітром.
У рівняннях зльоту важливо усвідомити, що, як зазначалося при першому представленні, відстань і прискорення вимірюються відносно землі; однак аеродинамічні сили в рівняннях, очевидно, залежать від швидкості польоту, а не від швидкості землі. Ми повинні враховувати це в наших рівняннях. При цьому ми будемо використовувати наступні позначення для різних швидкостей:
V G = ШВИДКІСТЬ ЗЕМЛІ
V A = ШВИДКІСТЬ ПОВІТРЯ
V W = ШВИДКІСТЬ ВІТРУ (ПАРАЛЕЛЬНО ЗЛІТНІЙ СМУЗІ)
Це дає
V A = V G ± V W (+ якщо зустрічний вітер, — якщо хвостовий вітер).
Повертаючись до основного рівняння руху, ми маємо
дВ Г/дТ = А — БВ А 2
Однак,
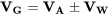
Таким чином
дВ Г/дТ = дВ А/дТ = А — БВ А 2.
Отже, для визначення часу зльоту ми використовуємо
dt = дВ А/(А — БВ А 2).
Щоб знайти відстань зльоту, ми використовуємо
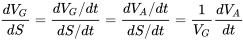
або
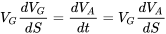
Це стає
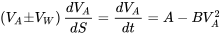
Нарешті, у нас є диференціал, який включає ефекти вітру. Ми напишемо його лише для випадку зустрічного вітру, оскільки це була б нормальна ситуація.
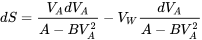
Тепер ми також повинні зазначити, що злітною швидкістю літака є повітряна швидкість, а не наземна. Рівняння часу та відстані вище можуть бути інтегровані вище, щоб дати
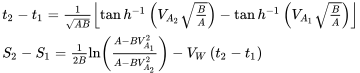
Нарешті, розуміючи, що зліт зазвичай починається з відпочинку з нульовою швидкістю землі (при t = 0), отримуємо
![t=1абтанн−1 (ВАТОБА) −тань−1 (VWBA)] S=12млрд (A−BVW2A−BVATO2) −VWT t=1абтанн−1 (ВАТОБА) −тань−1 (VWBA)] S=12млрд (A−BVW2A−BVATO2) −VWT](https://eng.libretexts.org/@api/deki/files/49408/79417f2457e4e5181a1778ee6cc11110.png)
Зауважте, що швидкість зльоту в цих рівняннях є повітряною швидкістю для зльоту, а не наземною швидкістю.
7.6 Посадка
Посадка, як і зліт, правильно визначена як має принаймні дві частини; «підхід» над 50-футовою перешкодою для приземлення та посадки. Вони, в свою чергу, можуть бути розділені на кілька інших сегментів. Підхід, як правило, не буде непотужним ковзанням, як вивчалося раніше. Нормальний підхід до посадки для більшості літаків - це силовий спуск. Визначення FAA приземного терміналу ковзання через перешкоду, однак, базується на непосиленому ковзанні як обмежувальному випадку. Ми вже розглядали планерний політ і повинні вміти справлятися з цією порцією польоту. Справжній спуск може бути найцікавішою частиною польоту для пілота, оскільки він виправляє бічні вітри, підйоми та вниз, націлившись на точку приземлення на злітно-посадковій смузі. Все це робиться зі швидкістю спуску близько 500 футів на хвилину (близько 8 миль/год).
Тут ми будемо турбувати себе тільки приземленням через повну зупинку ділянки посадки. Знову нашою першочерговою проблемою буде відстань наземного пробігу з надією, що повна зупинка відбудеться до кінця злітно-посадкової смуги.
Рівняння руху для посадкового наземного прогону ідентичні рівнянням для зльоту, однак терміни в рівняннях можуть припускати дуже різні величини від величин у зльоті. Для уповільнення літака в його посадці наземний запуск високий опір бажано, негативна або «зворотна» тяга може бути використана, і гальма будуть використовуватися під час більшої частини пробігу, щоб значно збільшити термін тертя. Граничні умови на інтегралах по суті змінюються, при цьому початкова швидкість - швидкість приземлення або «контакту», а кінцева швидкість землі дорівнює нулю; однак рішення може бути розбито на кілька сегментів, щоб врахувати послідовність подій як частина посадкового рулону.
Перш ніж ми розглянемо рівняння, давайте подивимося на типову посадку, яку бачить невеликий літак, пілот авіації загального призначення. Спуск наближення до посадки, ймовірно, буде здійснюватися з використанням повних стулок, принаймні в його остаточному «ковзанні» (це буде вірно практично для будь-якого літака). Це знизить швидкість стійла і дозволить наближатися і приземлятися з меншою швидкістю польоту. Це також посилить підхід ковзання і, на землі, додати до перетягування, щоб допомогти уповільнити літак.
Як тільки пілот відчує, що літак знаходиться під повним контролем після приземлення, він може підняти заслінки. Хоча це зменшує опір і сприяє більш тривалому рулону землі, це також зменшує підйом, збільшуючи сили тертя землі і дозволяючи краще керувати напрямком літака при боковому вітрі. Після цього гальма будуть застосовані для подальшого уповільнення літака до зупинки. Більший, реактивний літак може застосувати зворотну тягу дуже скоро після приземлення і перед використанням гальм для поліпшення уповільнення.
Тепер давайте знову подивимося на рівняння руху літака на землі. Ми все ще можемо використовувати
дС = ВДВ/(А — БВ 2).
Визначаємо V C як швидкість початкового контакту з землею при посадці в деякій точці, визначеній як S 1, і умови в наступній точці послідовності валка землі як S 2 і V. 2, даючи наступне інтегроване рівняння:
або
У рідкісному випадку, коли жоден з параметрів в рівнянні (T, μ, C Lg і т.д.) не змінюється під час наземного пробігу; тобто, де літак просто торкається вниз і берегів до зупинки, наша кінцева швидкість V 2 = 0, даючи
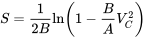
Для першої оцінки мінімального посадкового наземного пробігу можна було б припустити, що пілот здатний застосувати гальма майже миттєво після приземлення, і що тяга просто дорівнює нулю протягом усього рулону і, таким чином, використовувати вищевказане рівняння для обчислення відстані посадки. Насправді, як згадувалося раніше, ґрунтовий валок повинен бути визначений шляхом додавання ряду попередніх рівнянь Δ S, кожен з яких має відповідні початкові та кінцеві швидкості та значення тяги та тертя тощо.
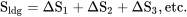
Час для посадки грунтового рулону знаходять від
дВ /дТ = А — БВ 2
або
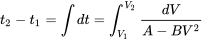
Інтеграція цього рівняння може приймати кілька різних форм залежно від відносних величин і знаків А і Б.
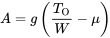
![b = ГВт [12ρ с (CD−мкГл) +а] b = ГВт [12ρ с (CD−мкГл) +а]](https://eng.libretexts.org/@api/deki/files/49415/3ca9ef333dce2343b151d0152f4bb5e6.png)
Зверніть увагу, що A майже завжди буде негативним, оскільки тяга завжди буде нульовою або негативною, якщо не при приземленні, то дуже швидко після цього. Гальмівні сили також можуть бути достатньо великими, щоб зробити B негативними, залежно від відносних величин коефіцієнтів підйому та опору. У різних ситуаціях посадки може бути можлива будь-яка комбінація негативних або позитивних термінів, і це впливає на форму інтеграла. Складність виникає в тому, що інтеграція дає квадратний корінь добутку A і B, а також інші терміни з квадратними коренями A і B окремо або співвідношеннями A і B. Результат може бути уявною відповіддю, якщо не вибрати правильне рішення.
Час посадки грунтового рулонного розчину наведено для чотирьох можливих комбінацій A і B нижче.
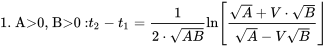 0, B>0:t2−t1=12⋅АБЛНА+В⋅ба-ВБ» назва =» 1. A>0, B> 0:t2−t1 = 12⋅ABLNA+v⋅ba−vb» клас =» математичний хакс» >
0, B>0:t2−t1=12⋅АБЛНА+В⋅ба-ВБ» назва =» 1. A>0, B> 0:t2−t1 = 12⋅ABLNA+v⋅ba−vb» клас =» математичний хакс» >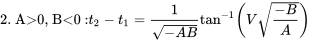 0, b<0:t2−t1=1−Abtan−1 (V−BA)» title=» 2. A> 0, B<0:t2−t1 = 1−Abtan−1 (V−BA)» клас =» математичний хакс» >
0, b<0:t2−t1=1−Abtan−1 (V−BA)» title=» 2. A> 0, B<0:t2−t1 = 1−Abtan−1 (V−BA)» клас =» математичний хакс» >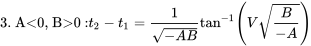 0:t2−t1 = 1−Abtan−1 (VB−A)» title=» 3. A0: t2−t1 = 1−абтан−1<0, B> (VB−A)» клас =» математика mathml» > <img src =» https://pressbooks.lib.vt.edu/app/up...f3594162d9.png» alt=» 4. A<0, b<0:t2−t1=12abln [V−B−AV−B+−A]» назва =» 4. А<0, Б
0:t2−t1 = 1−Abtan−1 (VB−A)» title=» 3. A0: t2−t1 = 1−абтан−1<0, B> (VB−A)» клас =» математика mathml» > <img src =» https://pressbooks.lib.vt.edu/app/up...f3594162d9.png» alt=» 4. A<0, b<0:t2−t1=12abln [V−B−AV−B+−A]» назва =» 4. А<0, Б
7.7 Вплив вітру на посадку Ground Roll
Як і у випадку зі зльотом, всі посадки повинні проводитися на вітер (за тими ж винятками, зазначеними для зльоту). Рівняння повинні бути записані, щоб врахувати різні терміни швидкості. Робиться це точно так, як це було для випадку зльоту.
дВ г/дС = (дВ г/дт)/(дС/дт) = [А — БВ А 2] /В г
або
V г (дВ г/дС) = А — БВ А 2 = V г (дВ г/дС)
Для випадку зустрічного вітру це дає:
(В А — В ш) (дВ А/дС) = А — БВ А 2
і
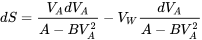
Інтегруючи і відзначаючи, що коли літак приїхав відпочивати на землі, швидкість буде дорівнює швидкості вітрової складової вздовж злітно-посадкової смуги V W,
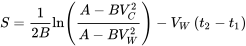
Останній член оцінюється за допомогою вже обговорюваного рівняння часу.
ПРИКЛАД 7.3
Наступний літак торкається при посадці зі швидкістю на 30% вище його стійлової швидкості. Пілот застосовує гальма, коли літак сповільнився до 80% швидкості приземлення. Якщо вітру немає, знайдіть відстань, необхідну для того, щоб літак прийшов до повної зупинки на злітно-посадковій смузі.
W = 30000 фунтів
μ B = 0,5
мк= 0,02
S = 750 кв.футів
C Lmax = 2,2 (з заслінками)
Припустімо, що коефіцієнт підйому та перетягування у 1,3 рази перевищує швидкість затримки, має значення восьми і є постійним протягом усього валка землі і що тяга дорівнює нулю при приземленні та по всьому рулону землі.
Оскільки все пов'язано зі швидкістю стійла, ми спочатку знайдемо її значення.
![Всталл = [2Вт/ (ρSCL)] 1/2 = 123,6 кадрів в секунду](https://eng.libretexts.org/@api/deki/files/49420/a50d2860baacd97492ac420f6066d42f.png)
даючи швидкість приземлення
V c = 1,3 В стійло = 160,7 кадрів в секунду
Ця швидкість дає коефіцієнт підйому
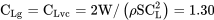
Будемо вважати, що цей коефіцієнт підйому постійний через наземний прогін.
Нам не дали полярне рівняння перетягування або його константи, але ми знаємо відношення підйому-перетягування і можемо знайти коефіцієнт опору та опору наступним чином:
Д ВК = Вт/ (Л/Д) = 3750 фунтів, С Дг = Д/ [½ ρ В С 2 С] = 0,1627.
Тепер ми можемо знайти терміни A і B для рішення відстані. Ми повинні вирішити для відстані в двох частинок, відстань між приземленням і застосуванням гальм і відстань, що залишилася до повної зупинки.
Перед гальмуванням
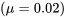
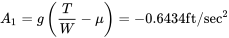
![B1 = ГВт [12ρ с (CD−мкСг) +а] = 1,3085 × 10−4фут-1 B1 = ГВт [12ρ с (CD−мкСг) +а] = 1,3085 × 10−4фут-1](https://eng.libretexts.org/@api/deki/files/49424/093837caf84035eb93769f4778eecd77.png)
даючи відстань
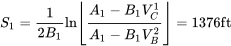
Після гальмування
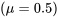
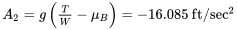
![B2 = ГВт [12ρ с (CD−мкБКЛ)] = 4,663 × 10−4фут-1 B2 = ГВт [12ρ с (CD−мкБКЛ)] = 4,663 × 10−4фут-1](https://eng.libretexts.org/@api/deki/files/49428/96e6342f412e609bf0c92194fb834880.png)
даючи решту відстані рулону землі, як:
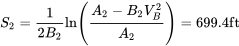
Загальний рулон землі при посадці становить суму двох відстаней вище:
S TOT = S 1 + S 2 = 2075,4 футів.
7.8 FAA ТА ІНШІ ВИЗНАЧЕННЯ ПАРАМЕТРІВ ЗЛЬОТУ І ПОСАДКИ
7.8.1 Зліт
Як обговорювалося раніше, існує безліч складових, які можуть бути включені в розрахунки злітно-посадкових відстаней. У попередніх розрахунках враховувалися лише фактичні відстані пробігу землі, і вони, особливо під час посадки, можуть складатися з декількох сегментів, де застосовуються різні значення коефіцієнта тертя та тяги. Повний погляд на зліт також повинен включати відстань між ініціацією обертання та встановленням постійної швидкості підйому та відстань, необхідну для очищення певної висоти перешкоди, як показано на малюнку нижче.
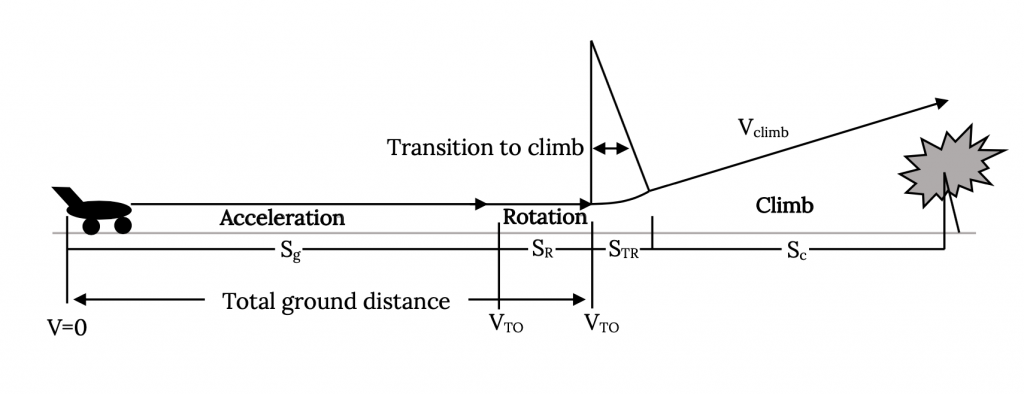
Кілька різних термінів можуть бути використані в повному обговоренні зльоту. До них відносяться наступні:
Ground Roll: Відстань від початку наземного ходу або відпуску гальм до точки, де колеса залишають землю. Сюди входить відстань, необхідна для досягнення необхідного підйому, щоб дорівнювати вазі під час обертання. Швидкість зльоту повинна бути щонайменше в 1,1 рази більше швидкості затримки і зазвичай визначається як від 1,1 до 1,2 рази більше швидкості.
Відстань зазору перешкод: Відстань між точкою відпуску гальма та тією, де досягається задана висота. Ця висота зазвичай визначається як 50 футів для військових або менших літаків цивільної авіації та 35 футів для комерційних літаків.
Збалансована довжина поля: довжина поля, необхідна для безпечного завершення зльоту, якщо один двигун на багатомоторному літаку вийде з ладу в найгірший можливий час під час зльоту. Ця відстань включає відстань зазору перешкоди. Збалансовану довжину поля іноді також називають довжиною поля зльоту FAR, оскільки це вимога для сертифікації FAA в FAR 25 для комерційних літаків і включає 35 футів зазору перешкод мінімум. У ранній частині зльоту наземного запуску втрата одного двигуна зазвичай призведе до рішення перервати зліт, застосувати гальма і прийти до зупинки. «Найгіршим можливим часом» для виходу з ладу двигуна було б тоді, коли вже неможливо зупинити літак до кінця злітно-посадкової смуги, і необхідно прийняти рішення продовжити зліт з одним двигуном.
Швидкість прийняття рішення (V 1 ): Швидкість, з якою відстань зупиняється після відмови одного двигуна точно дорівнює відстані для продовження зльоту на інших двигунів та очищення визначених FAA перешкод. При розрахунку цієї швидкості не можна припускати можливість використання зворотної тяги як частини гальмівного процесу.
7.8.2 Посадка
Як і при зльоті, посадка включає кілька можливих відрізків, як показано на малюнку 7.3. Наші попередні розрахунки включали лише фактичну відстань рулону землі, але повне визначення може також включати частину підходу, необхідного для очищення певної перешкоди, і яка необхідна для переходу від стійкого ковзання підходу до приземлення («відстань спалаху»). Зверніть увагу, що посадковий наземний прогін також може включати ділянки зі зворотною тягою, що використовуються окремо або з гальмами.
Вага літака при посадці, як правило, менше, ніж при зльоті через використання палива під час польоту, однак зазвичай обчислювати відстань посадки навчально-тренувального літака та більшості повітряних суден, керованих гвинтом, при злітній вазі. Для струменів, що не тренуються, вага посадки зазвичай вважається 85% від злітної маси. Військові вимоги зазвичай припускають посадку з повним корисним навантаженням і приблизно половиною палива.
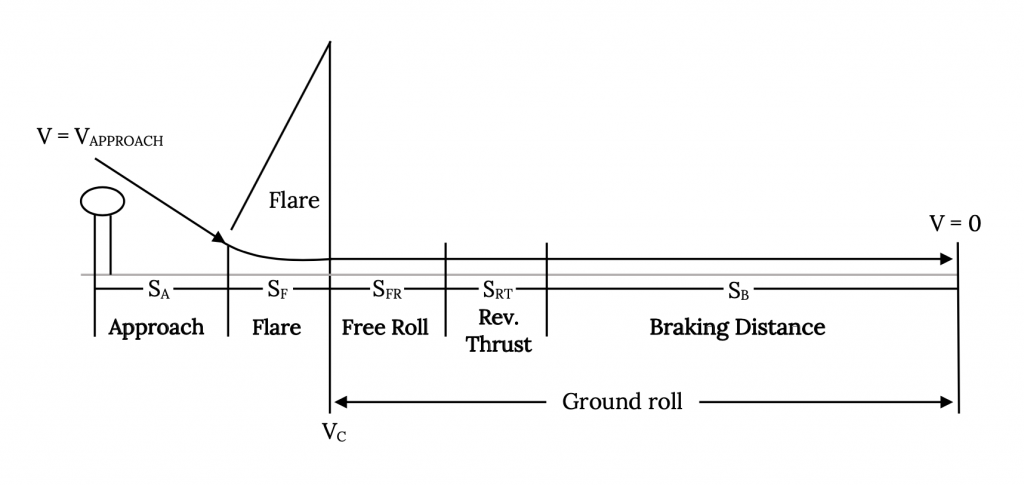
Як і при зльоті, існує кілька визначень, пов'язаних з посадкою, які повинні бути знайомі інженера-виконавцю:
FAR 23 Довжина посадочного поля: Ця відстань включає в себе те, що необхідно очистити 50-футову перешкоду на швидкості наближення, що летить вниз за певним підходом glidepath (зазвичай близько 3 градусів). Touchdown зазвичай приблизно в 1,15 рази перевищує швидкість затримки. Ця загальна відстань, як правило, приблизно вдвічі перевищує розрахункову відстань рулону землі. Ця відстань зазвичай приблизно така ж, як зазначена в запитах на пропозиції щодо військових літаків.
Довжина посадкового поля FAR25: Ця відстань додає до відстані FAR 23 вище довільних двох третин як запас міцності.
Домашнє завдання 7
1. Літак має наступні технічні характеристики:
Ш = 24,000 фунтів
S = 600 футів 2
С Д0 = 0,02
К = 0,056
У цього літака закінчилося паливо на висоті 30 000 футів. Знайдіть початкові та кінцеві значення його швидкості польоту для найкращого діапазону, кут ковзання для найкращого діапазону, швидкість спуску на цій швидкості та час, необхідний для спуску до рівня моря з цією швидкістю.
2. Для літака вище припустимо тягу рівня моря 6000 фунтів і припустимо, що тяга на висоті дорівнює тязі рівня моря, що разів коефіцієнт щільності (сигма). Знайдіть справжні повітряні швидкості для найкращої швидкості підйому на рівні моря, на 20 000 футів, 30 000 футів та 40 000 футів. Також знайдіть висоту стелі.
3. Для літака, де:
Ш = 10,000 фунтів
Вт/с = 50 фунтів на дюйм
С Д0 = 0,015
К = 0,02
Знайдіть найкращу швидкість підйому та швидкість для найкращої швидкості підйому на рівні моря, де T = постійна = 4000 фунтів і на висоті 40 000 футів, де T = 2000 фунтів.
Посилання
Малюнок 7.1: Родинний сірий (2021). «Сили на літаку при зльоті або посадці». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/7.1-updated
Малюнок 7.2: Родинний сірий (2021). «Злітні сегменти». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/7.2-updated
Малюнок 7.3: Родинний сірий (2021). «Посадочні сегменти». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/7.3-updated
<! — pb_fixme —><! — pb_fixme —>
