Skip to main content
LibreTexts - Ukrayinska

7.5: Центр мас

  1. Last updated
  2. Save as PDF
  • Page ID
    74999

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Визначте центр мас для об'єкта з безперервним розподілом маси

    У попередніх модулів на тему «Центр мас і поступального руху» ми дізналися, чому концепція центру маси (СОМ) допомагає вирішувати механічні завдання, пов'язані з твердим тілом. Тут ми вивчимо суворе визначення СОМ і способи його визначення. Положення СОМ є середньозваженим по масі положень частинок.

    Визначення: центр мас

    Центр мас - це твердження просторового розташування маси (тобто розподілу маси всередині системи). Положення СОМ дається математична формулювання, яка передбачає розподіл маси в просторі:

    \[\mathrm{r_{COM}=\dfrac{∑_i m_ir_i}{M},}\]

    де r COM і r i - вектори, що представляють положення COM і i-ї частинки відповідно, а M і mi - загальна маса і маса i-ї частинки відповідно. Це означає, що положення СОМ є середньозваженим по масі положень частинок.

    Об'єкт з безперервним розподілом маси

    Якщо розподіл маси є безперервним з щільністю ρ (r) в межах об'єму V, положення СОМ задається як

    \[\mathrm{r_{COM}=\dfrac{1}{M} \int _V ρ(r)rdV,}\]

    де M - загальна маса в обсязі. Якщо безперервний розподіл маси має рівномірну щільність, що означає ρ постійний, то центр маси такий же, як і центр об'єму.

    Розташування Центру Мас

    Експериментальне визначення центру мас тіла використовує сили тяжіння на тілі і спирається на те, що в паралельному полі тяжіння поблизу поверхні Землі центр мас такий же, як центр ваги.

    Центр маси тіла з віссю симетрії і постійної щільності повинен лежати на цій осі. Таким чином, центр мас круглого циліндра постійної щільності має свій центр маси на осі циліндра. Таким же чином центр маси сферично симетричного тіла постійної щільності знаходиться в центрі сфери. Загалом, для будь-якої симетрії тіла його центр маси буде фіксованою точкою цієї симетрії.

    У двох вимірах: експериментальним методом визначення місця розташування центру мас є призупинення об'єкта з двох місць і скидання схилів з точок підвісу. Перетин двох ліній - центр мас.

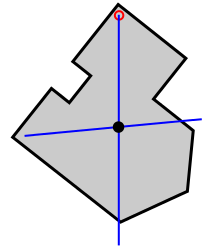
    зображення

    Метод схилу для центру маси: Призупинення об'єкта з двох місць і скидання схилів з точок підвісу. Перетин двох ліній - центр мас.

    У трьох вимірах: Підтримуючи об'єкт у трьох точках та вимірюючи сили, що чинять опір вазі об'єкта, можна визначити COM тривимірних координат центру мас.

    Рух центру мас

    Ми можемо описати поступальний рух твердого тіла так, ніби це точкова частинка із загальною масою, розташованої в COM-центрі мас.

    навчальні цілі

    • Вивести центр маси для поступального руху твердого тіла

    Ми можемо описати поступальний рух твердого тіла так, ніби це точкова частинка із загальною масою, розташованої в центрі мас (СОМ). У цьому атом. ми доведемо, що сумарна маса (М) разів перевищує прискорення СОМ (а СОМ), дійсно, дорівнює сумі зовнішніх сил. Тобто,

    \[\mathrm{M \cdot a_{COM}=∑F_{ext}.}\]

    Можна помітити, що 2-й закон Ньютона застосовується так, ніби ми описуємо рух точкової частинки (з масою М) під впливом зовнішньої сили.

    деривація

    З визначення центру мас,

    \[\mathrm{r_{COM}=\dfrac{∑_i m_ir_i}{M},}\]

    ми отримуємо\(\mathrm{M⋅a_{COM}=∑m_ia_i}\), приймаючи похідну часу двічі з кожного боку.

    Зауважте, що\(\mathrm{∑m_ia_i=∑F_i}\).

    У системі частинок кожна частинка може відчувати як зовнішні, так і внутрішні сили. Тут зовнішні сили - це сили від зовнішніх джерел, тоді як внутрішні сили - сили між частинками в системі. Оскільки сума всіх внутрішніх сил буде дорівнює 0 завдяки 3-му закону Ньютона,

    \(\mathrm{∑F_i=∑F_{i,ext}}\). Тому отримуємо\(\mathrm{M \cdot a_{COM}=∑F_{ext}.}\)

    Наприклад, коли ми обмежуємо нашу систему Землею і Місяцем, гравітаційна сила, обумовлена Сонцем, була б зовнішньою, тоді як гравітаційна сила на Землі через Місяць (і навпаки) була б внутрішньою. Так як сили гравітації між Землею і Місяцем рівні за величиною і протилежні в напрямку, вони скасують один одного в сумі (див.).

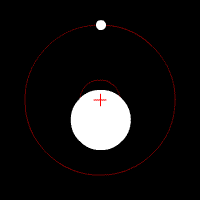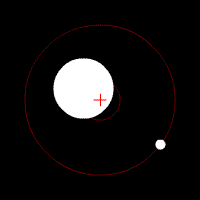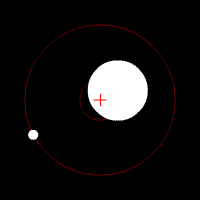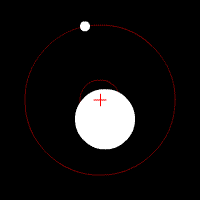
    зображення

    COM Землі і Місяця: Земля і Місяць, що обертаються навколо COM всередині Землі. Червоний хрест являє собою СОМ двотільної системи. COM буде обертатися навколо Сонця так, ніби це точкова частка.

    Слідство

    Коли зовнішньої сили немає, імпульс COM зберігається.

    Доказ: Оскільки зовнішньої сили немає,\(\mathrm{M \cdot a_{COM}=0}\). Тому

    \(\mathrm{M \cdot v_{COM}=constant.}\)

    Доказ

    Так як зовнішньої сили немає,

    \[M⋅a_{COM}=0.\]

    Тому

    \(M⋅v_{COM}=constant\).

    \(\square\)

    Центр маси людського тіла

    Центр маси (СОМ) є важливою фізичною концепцією - це точка, навколо якої обертаються об'єкти.

    навчальні цілі

    • Оцініть COM заданого об'єкта

    Центр мас (СОМ) - важливе фізичне поняття. Це точка на об'єкті, в якій зважене відносне положення розподіленої маси дорівнює нулю - точці, навколо якої обертаються об'єкти.

    Людські пропорції були важливими в мистецтві, вимірюванні та медицині (добре відомий малюнок людського тіла видно в). Хоча людський організм має складні особливості, розташування центру маси (СОМ) може бути хорошим показником пропорцій тіла. Центр маси людського тіла залежить від статі і положення кінцівок. У стоячій позі він, як правило, приблизно на 10 см нижче пупка, біля верхньої частини тазостегнових кісток. У цьому атомі ми навчимося вимірювати СОМ людського тіла.

    зображення

    Леонардо да Вінчі «Вітрувіанська людина»: Вітрувіанська людина: малюнок, створений Леонардо да Вінчі. Малюнок заснований на кореляціях ідеальних людських пропорцій з геометрією, описаної давньоримським архітектором Вітрувієм у книзі III його трактату De Architectura.

    Приклад\(\PageIndex{1}\):

    Для початку візьмемо дві шкали і дерев'яний брус (Н метр завдовжки), досить довгий, щоб вмістити все тіло предмета. Поставте ваги H метрів один від одного, і розмістіть промінь поперек ваг, як показано в. Тепер нехай предмет лежить на балці. Переконайтеся, що його/її п'яти вирівняні з одним кінцем пучка. Виміряйте показання (F 1, F 2) на шкалі.

    зображення

    COM людського тіла: Ця цифра демонструє вимірювання COM людського тіла.

    Система (людина+промінь) має три зовнішні сили: гравітацію на предмет (F СМ), і нормальні сили від шкал F 1 і F 2. Рівняння руху для сили (F = мА) дасть нам:

    \[\mathrm{F1+F2=Mg,}\]

    де M - маса предмета. (Ми припускаємо, що дерев'яна балка не має маси.) Це рівняння не надає всієї інформації для визначення місця COM. Однак рівняння руху для крутного моменту\(\mathrm{(τ=Iα)}\) допомагає.

    Так як чистий крутний момент системи дорівнює нулю (звідси немає прискорення обертання),

    \[\mathrm{hF_2−(H−h)F_1=0. (h: COM \; height)}\]

    В якості походження крутного моменту вибирається СОМ. Тому гравітація нічого не сприяє як крутний момент. Вирішуючи для h і використовуючи рівняння руху для сили, отримаємо

    \[\mathrm{h=\dfrac{HF_1}{Mg}.}\]

    Центр маси і поступального руху

    СОМ (центр маси) системи частинок - це геометрична точка, яка приймає на себе всю масу і зовнішню силу (и) під час руху.

    навчальні цілі

    • Підтримка наявності СОМ в тривимірних тілах в русі

    Вступ: COM, лінійний імпульс та зіткнення

    Наше вивчення руху було обмежено до цього моменту. Ми так само посилалися на частинку, об'єкт і тіло. Ми вважали, що фактичні тривимірні тверді тіла рухаються таким чином, що всі складові частинки мали однаковий рух (тобто однакову траєкторію, швидкість і прискорення). Роблячи це, ми по суті розглядали тверде тіло як точкову частинку.

    Центр маси (COM)

    Однак фактичне тіло може рухатися інакше, ніж ця спрощена парадигма. Розглянемо кульку, що котиться по похилій площині або палицю, кинуту в повітря. Різні частини тіла мають різні рухи. Під час перекладу в повітрі палиця обертається навколо рухомої осі, як показано на. Це означає, що такі тіла можуть не вести себе як точкова частка, як було запропоновано раніше.

    зображення

    Сили на COM: Зліва: Сила, здається, працює на COM є «mgsinθ. Праворуч: Сила, здається, діє на COM - «mg».

    Описати рухи частин або частинок, які мають різні рухи, було б досить складно зробити комплексно. Однак такі тривимірні тіла в русі мають одну дивовижну, спрощуючу характеристику - геометричну точку, яка поводиться як частинка. Ця точка відома як центр маси, скорочено COM (математичне визначення COM буде введено в наступному атомі на «Розташування центру мас»). Він має наступні два характеризують аспекти:

    • Центр маси, здається, несе всю масу тіла.
    • У центрі маси з'являються всі зовнішні сили.

    Важливо, що центр кулі (COM рухомого кулі) слідує прямий лінійний шлях; тоді як COM палиці слідує параболічним шляхом (як показано на малюнку вище). По-друге, сили, здається, діють на COM у двох випадках («mgsinθ та «mg») так, ніби вони дійсно були частиноподібними об'єктами. Таким чином, ця концепція COM усуває складності, інакше присутні при спробі описати рухи жорстких тіл.

    Опис руху в жорсткому тілі

    Загальний рух об'єкта (з масою m) ми можемо описати наступним чином:

    • Ми описуємо поступальний рух твердого тіла так, ніби це точкова частинка з масою m, розташована на COM.
    • Обертання частинки, по відношенню до СОМ, описується самостійно.

    «Відокремлюємо» поступальну частину руху від обертальної частини. Впроваджуючи поняття СОМ, поступальний рух стає точковою частинкою з масою m, що значно спрощує математичну складність задачі.

    Ключові моменти

    • Центр мас (СОМ) - це твердження просторового розташування маси (тобто розподілу маси всередині системи).
    • Експериментальне визначення центру маси тіла використовує сили тяжіння на тілі і спирається на те, що в паралельному полі тяжіння поблизу поверхні землі центр маси такий же, як центр ваги.
    • Для 2D об'єкта експериментальним методом визначення місця розташування центру мас є призупинення об'єкта з двох місць і скидання схилів з точок підвісу. Перетин двох ліній - центр мас.
    • Загальна маса разів на прискорення центру мас дорівнює сумі зовнішніх сил.
    • Для поступального руху твердого тіла з масою М застосовується 2-й закон Ньютона так, ніби ми описуємо рух точкової частинки (з масою М) під впливом зовнішньої сили.
    • Коли зовнішньої сили немає, центр імпульсу маси зберігається.
    • Хоча людське тіло має складні особливості, розташування центру маси (СОМ) може бути хорошим показником пропорцій тіла.
    • Ми можемо виміряти розташування СОМ двома шкалами і дерев'яним брусом. Лінійні та обертальні рівняння руху дають нам місце розташування.
    • Центр маси людського тіла залежить від статі і положення кінцівок. У стоячій позі він, як правило, приблизно на 10 см нижче пупка, біля верхньої частини тазостегнових кісток.
    • При русі твердого тіла різні частини тіла мають різні рухи. Це означає, що ці тіла можуть не вести себе як точкова частинка.
    • Існує характерна геометрична точка тривимірного тіла в русі. Ця точка поводиться як частинка, і відома як центр маси, скорочено COM. СОМ, здається, несе всю масу тіла. Всі зовнішні сили, здається, застосовуються на COM.
    • Для опису руху твердого тіла (з можливою складною геометрією) відокремлюємо поступальну частину руху від обертальної частини.

    Ключові умови

    • схил: Шнур з прикріпленим вагою, використовується для виготовлення вертикальної лінії.
    • жорстке тіло: ідеалізоване тверде тіло, розмір і форма якого фіксовані і залишаються незмінними при застосуванні сил; використовується в ньютонівській механіці для моделювання реальних об'єктів.
    • центр маси: Центр маси (COM) - це унікальна точка в центрі розподілу маси в просторі, яка має властивість, що зважені вектори положення відносно цієї точки дорівнюють нулю.
    • крутний момент: обертальний або скручувальний ефект сили; (СІ одиниця Ньютон-метр або Нм; імперська одиниця фут-фунт або фут-фунт)
    • точкова частинка: ідеалізація частинок, що сильно використовуються у фізиці. Його визначальною особливістю є те, що їй не вистачає просторового розширення, що означає, що геометрично частка еквівалентна точці.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ