12.3: Теплове розширення

Last updated

Oct 27, 2022
Save as PDF
- 12.2: Температурні та температурні шкали
- 12.4: Закон про ідеальний газ

Boundless
Boundless

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

цілі навчання

Опишіть зміни обсягу, що відбуваються у відповідь на зміну температури

Теплове розширення - це тенденція речовини до зміни обсягу у відповідь на зміну температури. (Прикладом цього є вигин залізничної колії, як видно в.) Атоми і молекули в твердому тілі, наприклад, постійно коливаються навколо своєї точки рівноваги. Такий вид збудження називається тепловим рухом. При нагріванні речовини його складові частинки починають більше рухатися, тим самим підтримуючи більший середній поділ з сусідніми частинками. Ступінь розширення, поділена на зміну температури, називається коефіцієнтом теплового розширення матеріалу; він, як правило, змінюється залежно від температури.

зображення

Рис. 1: Теплове розширення довгих безперервних ділянок залізничних колій є рушійною силою для вигину рейок. Це явище призвело до 190 з'їздів поїздів протягом 1998-2002 тільки в США.

Теплове розширення: Короткий вступ до теплового розширення для студентів.

Розширення, а не скорочення

Чому матерія зазвичай розширюється при нагріванні? Відповідь можна знайти у формі типового потенціалу частинки-частинки в речовині. Частинки в твердих тілах і рідинях постійно відчувають присутність інших сусідніх частинок. Ця взаємодія може бути зображена математично у вигляді кривої потенціалу. Рис. 2 ілюструє, як цей міжчастинковий потенціал зазвичай приймає асиметричну форму, а не симетричну форму, як функцію відстані частинок до частинки. Зверніть увагу, що крива потенціалу крутіша для меншої відстані. На схемі (б) показано, що при нагріванні речовини збільшується рівноважна (або середня) відстань частинки-частинки. Матеріали, які стискаються або підтримують свою форму з підвищенням температури, зустрічаються рідко. Цей ефект обмежений в розмірах, і відбувається лише в межах обмежених температурних діапазонів.

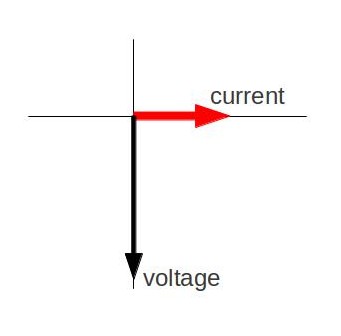
зображення

Рис. 2: Типовий міжчастинковий потенціал у конденсованому середовищі (наприклад, твердому або рідкому).

Лінійне розширення

До першого наближення зміна вимірювань довжини об'єкта (лінійний розмір на відміну від, наприклад, об'ємного розміру) внаслідок теплового розширення пов'язано зі зміною температури на коефіцієнт лінійного розширення. Це дробове зміна довжини на градус зміни температури. Припускаючи незначний вплив тиску, ми можемо написати:

$\mathrm{α_L=\dfrac{1}{L}\dfrac{dL}{dT},}$

де $\mathrm{L}$ вимірюється конкретна довжина і $\mathrm{\frac{dL}{dT}}$ швидкість зміни цього лінійного виміру на одиницю зміни температури. З визначення коефіцієнта розширення зміна лінійного розміру $\mathrm{ΔL}$ в діапазоні температур $\mathrm{ΔT}$ можна оцінити як:

$\mathrm{\dfrac{ΔL}{L}=α_LΔT.}$

Це рівняння працює добре до тих пір, поки коефіцієнт лінійного розширення не сильно змінюється над зміною температури. Якщо це так, рівняння має бути інтегроване.

Розширення площі

Об'єкти розгортаються у всіх вимірах. Тобто їх площі і обсяги, а також їх довжини збільшуються з температурою.

цілі навчання

Висловіть коефіцієнт теплового розширення площі у вигляді рівняння

Ми дізналися про лінійному розширенні (в одному вимірі) в попередньому Атомі. Об'єкти розширюються у всіх розмірах, і ми можемо розширити теплове розширення для 1D до двох (або трьох) розмірів. Тобто їх площі і обсяги, а також їх довжини збільшуються з температурою.

Вікторина

Перш ніж розбиратися в подробицях, ось цікаве питання. Уявімо, що у нас прямокутний лист металу з круглим отвором посередині. Якщо метал нагрівається, можна здогадатися, що шматок, в общем-то, вийде більше за рахунок теплового розширення. Тепер, що буде з круглим отвором посередині? Чи буде отвір більшим чи меншим? Відповідь: Уявіть, що у нас подібний металевий лист, але без отвору. Намалюйте уявну кругову лінію, що представляє круглий отвір у нашій вікторині. Як змінюється цей уявний коло в міру нагрівання металу? Так. Він стане більше. Тому можна здогадатися, що діра в нашій вікторині вийде більше.

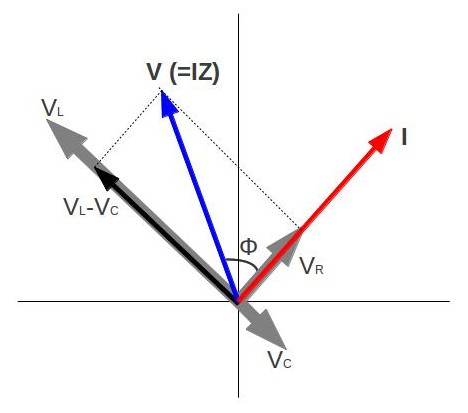
зображення

Рис. 1: Загалом об'єкти розширюються у всіх напрямках з підвищенням температури. На цих кресленнях початкові межі об'єктів показані суцільними лініями, а розширені межі пунктирними лініями. (a) Площа збільшується, оскільки збільшуються як довжина, так і ширина. Збільшується і площа круглої пробки. (b) Якщо пробку видалити, отвір, який вона залишає, стає більшим із збільшенням температури, так само, як якщо б розширюється пробка все ще на місці.

Коефіцієнт теплового розширення площі

Коефіцієнт теплового розширення площі пов'язує зміну розмірів площі матеріалу зі зміною температури. Це дробове зміна площі на градус зміни температури. Ігноруючи тиск, ми можемо написати: $\mathrm{α_A=\dfrac{1}{A}\dfrac{dA}{dT}}$ , де знаходиться якась область інтересу на об'єкті, і $\mathrm{\frac{dA}{dT}}$ є швидкість зміни цієї площі на одиницю зміни температури. Зміна лінійного виміру можна оцінити як: $\mathrm{\frac{ΔA}{A}=α_AΔT}$ . Це рівняння працює добре до тих пір, поки коефіцієнт лінійного розширення не сильно змінюється над зміною температури $\mathrm{ΔT}$ . Якщо це так, рівняння має бути інтегроване.

Зв'язок з коефіцієнтом лінійного теплового розширення

Для ізотропних матеріалів, а для невеликих розширень коефіцієнт лінійного теплового розширення становить половину коефіцієнта площі. Щоб вивести співвідношення, візьмемо квадрат зі сталі, який має сторони довжини L. Початкова площа буде $\mathrm{A = L^2}$ , а нова площа, після підвищення температури, буде

$\begin{align} \mathrm{A+ΔA} & \mathrm{=(L+ΔL)^2} \\ & \mathrm{=L^2+2LΔL+(ΔL)^2} \\ & \mathrm{≈L^2+2LΔL} \\ & \mathrm{=A+2A\dfrac{ΔL}{L}} \end{align}$

Наближення тримає для досить невеликого $\mathrm{ΔL}$ campared до $\mathrm{L}$ . Так як $\mathrm{\dfrac{ΔA}{A}=2\dfrac{ΔL}{L}}$ з рівняння вище (і з визначень теплових коефіцієнтів), отримаємо $\mathrm{α_A=2_{αL}}$ .

Розширення гучності

Речовини розширюються або стискаються при зміні їх температури, при цьому розширення або скорочення відбуваються у всіх напрямках.

цілі навчання

Порівняйте вплив тиску на розширення газоподібних і твердих матеріалів

Коефіцієнт об'ємного теплового розширення є самим основним коефіцієнтом теплового розширення. ілюструє, що в цілому речовини розширюються або стискаються при зміні їх температури, при цьому розширення або стиснення відбуваються у всіх напрямках. Такі речовини, які розширюються в усіх напрямках, називаються ізотропними. Для ізотропних матеріалів площа і лінійні коефіцієнти можуть бути розраховані з об'ємного коефіцієнта (розглянуто нижче).

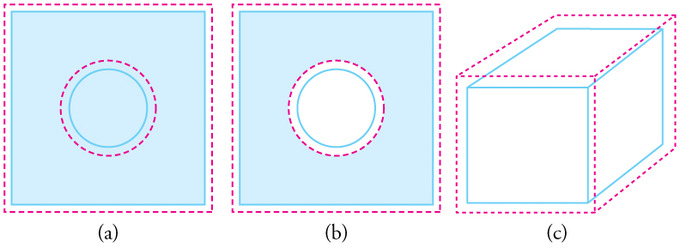
зображення

Об'ємне розширення: Загалом, об'єкти розширюються у всіх напрямках із збільшенням температури. На цих кресленнях початкові межі об'єктів показані суцільними лініями, а розширені межі пунктирними лініями. (a) Площа збільшується, оскільки збільшуються як довжина, так і ширина. Збільшується і площа круглої пробки. (b) Якщо пробку видалити, отвір, який вона залишає, стає більшим із збільшенням температури, так само, як якщо б розширюється пробка все ще на місці. (c) Обсяг також збільшується, тому що всі три виміри збільшуються.

Теплове розширення - розширення обсягу: Короткий вступ до теплового розширення для студентів.

Математичні визначення цих коефіцієнтів визначені нижче для твердих тіл, рідин і газів:

$\mathrm{α_V=\dfrac{1}{V}(\dfrac{∂V}{∂T})p.}$

Індексит р вказує на те, що тиск тримається постійним під час розширення. У випадку з газом важливий той факт, що тиск тримається постійним, оскільки обсяг газу буде помітно змінюватися як з тиском, так і з температурою.

Для твердої речовини можна ігнорувати вплив тиску на матеріал, таким чином можна записати об'ємний коефіцієнт теплового розширення:

$\mathrm{α_V=\dfrac{1}{V}\dfrac{dV}{dT},}$

де V - об'єм матеріалу, а дВ/dT швидкість зміни цього обсягу з температурою. Це означає, що обсяг матеріалу змінюється на якусь фіксовану дробову кількість. Наприклад, сталевий блок об'ємом 1 кубічний метр може збільшитися до 1,002 кубічних метрів при підвищенні температури на 50° C, тобто розширення на 0,2%. Об'ємний коефіцієнт розширення становив би 0,2% для 50° C, або 0,004% на градус С.

Зв'язок з коефіцієнтом лінійного теплового розширення

Для ізотропного матеріалу, а для невеликих розширень коефіцієнт лінійного теплового розширення становить третину об'ємного коефіцієнта. Щоб вивести співвідношення, візьмемо куб сталі, який має сторони довжини L. Початковий обсяг буде $\mathrm{V = L^3}$ , а новий обсяг, після підвищення температури, буде:

$\begin{align} \mathrm{V+ΔV} & \mathrm{=(L+ΔL)^3} \\ & \mathrm{=L^3+3L^2ΔL+3L(ΔL)^2+(ΔL)^3} \\ & \mathrm{≈L^3+3L^2ΔL} \\ & \mathrm{=V+3V\dfrac{ΔL}{L}.} \end{align}$

Апроксимація тримає для досить малого $\mathrm{ΔL}$ порівняно з Л.

$\mathrm{\dfrac{ΔV}{V}=3\dfrac{ΔL}{L}}$

(І з визначень теплових коефіцієнтів) приходимо до:

$\mathrm{α_V=3α_L}$

Особливі властивості води

Об'єкти будуть розширюватися з підвищенням температури, але вода - найважливіший виняток із загального правила.

цілі навчання

Опишіть властивості теплового розширення води

Особливі властивості води

Загалом, предмети будуть розширюватися з підвищенням температури. Однак ряд матеріалів укладаються на опалення в певних діапазонах температур; це зазвичай називають негативним тепловим розширенням, а не «тепловим стисканням» Вода є найважливішим винятком із загального правила. Вода має цю унікальну характеристику через особливу природу водневого зв'язку в H ₂ O.

Щільність води при зміні температури

При температурі понад 4ºC (40ºF) вода розширюється зі збільшенням температури (її щільність зменшується). Однак він розширюється зі зменшенням температури, коли вона становить від +4ºC до 0ºC (від 40ºF до 32ºF). Вода найщільніша при +4ºC.

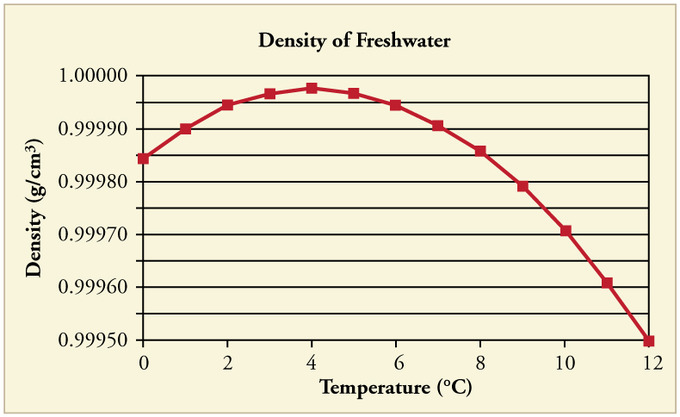
зображення

Щільність води проти температури: Щільність води як функція температури. Відзначимо, що теплове розширення насправді дуже мало. Максимальна щільність при+4ºC лише на 0,0075% більша, ніж щільність при 2ºC, і на 0,012% більше, ніж при 0ºC.

Мабуть, найяскравішим ефектом цього явища є замерзання води у водоймі. Коли вода біля поверхні охолоджується до 4ºC, вона щільніше, ніж вода, що залишилася, і таким чином опуститься на дно. Цей «оборот» призводить до того, що біля поверхні утворюється шар більш теплої води, який потім охолоджується. Зрештою ставок має рівномірну температуру 4ºC. Якщо температура в поверхневому шарі опускається нижче 4ºC, вода менш щільна, ніж вода нижче, і, таким чином, залишається біля верху.

В результаті поверхня ставка може повністю замерзнути, тоді як дно може залишатися на рівні 4ºC. Лід поверх рідкої води забезпечує ізоляційний шар від суворих температур зовнішнього повітря взимку. Риби та інші водні мешканці можуть вижити у воді 4ºC під льодом, завдяки цій незвичайній характеристиці води. Він також виробляє циркуляцію води в ставку, яка необхідна для здорової екосистеми водойми.

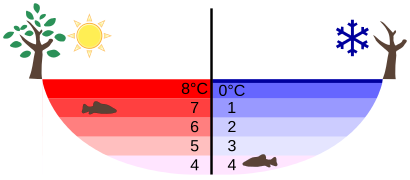
зображення

Температура в озері: Розподіл температури в озері в теплі і холодні дні взимку

Лід проти води

Тверда форма більшості речовин щільніше рідкої фази; таким чином, блок більшості твердих речовин буде занурюватися в рідину. Однак брила льоду плаває в рідкій воді, оскільки лід менш щільний. При замерзанні щільність води зменшується приблизно на 9%.

Ключові моменти

Міжчастинковий потенціал зазвичай приймає асиметричну форму, а не симетричну форму як функцію відстані частинки-частинки. Ось чому питання розширюється і стискається при зміні температури.
Зміна вимірювань довжини об'єкта внаслідок теплового розширення пов'язана зі зміною температури на «коефіцієнт лінійного розширення», який задається як $\mathrm{α_L=\dfrac{1}{L} \dfrac{dL}{dT}}$ .
Коефіцієнт лінійного розширення є наближенням лише за вузьким температурним інтервалом.
Коефіцієнт теплового розширення площі пов'язує зміну розмірів площі матеріалу зі зміною температури. Він визначається як $\mathrm{α_A=\dfrac{1}{A}\dfrac{dA}{dT}}$ .
Співвідношення між площею і коефіцієнтом лінійного теплового розширення наведено наступним чином: $\mathrm{α_A=2α_L}$ .
Подібно до коефіцієнта лінійного розширення, коефіцієнт теплового розширення площі працює як наближення лише у вузькому температурному інтервалі.
Речовини, що розширюються з однаковою швидкістю в кожну сторону, називаються ізотропними.
У випадку з газом розширення залежить від того, як змінився тиск в процесі, оскільки обсяг газу буде значно змінюватися залежно від тиску, а також температури.
Для твердого тіла ми можемо ігнорувати вплив тиску на матеріал, а об'ємний коефіцієнт теплового розширення можна записати як $\mathrm{α_V=\dfrac{1}{V}\dfrac{dV}{dT}}$ . Для ізотропних матеріалів, $\mathrm{α_V=3α_L}$ .
Вода розширюється зі збільшенням температури (її щільність зменшується), коли вона знаходиться при температурі більше 4ºC (40ºF). Однак він розширюється зі зменшенням температури, коли вона становить від +4ºC до 0ºC (від 40ºF до 32ºF). Вода найщільніша при +4ºC.
Завдяки своєрідній властивості теплового розширення води, поверхня ставка може повністю замерзнути, тоді як дно може залишатися на рівні 4ºC. Риби та інші водні мешканці можуть вижити у воді 4ºC під льодом, завдяки цій незвичайній характеристиці води.
Тверда форма більшості речовин щільніше рідкої фази; таким чином, блок більшості твердих речовин буде занурюватися в рідину. Однак брила льоду плаває в рідкій воді, оскільки лід менш щільний.

Ключові умови

potential: крива, що описує ситуацію, коли різниця потенційних енергій об'єкта в двох різних положеннях залежить тільки від цих позицій.
коефіцієнт лінійного теплового розширення: Дробова зміна довжини на ступінь зміни температури.
ізотропний: Маючи властивості, однакові у всіх напрямках; проявляючи ізотропію.
водневий зв'язок: Слабкий зв'язок, в якій атом водню в одній молекулі притягується до електронегативного атома (зазвичай азоту або кисню) в тій же або іншій молекулі.

ЛІЦЕНЗІЇ ТА АВТОРСТВА

CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

Курація та доопрацювання. Надано: Boundless.com. Ліцензія: CC BY-SA: Із Зазначенням Авторства

CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ

Теплове розширення. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Thermal_Expansion. Ліцензія: CC BY-SA: Із Зазначенням Авторства
потенціал. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Потенціал. Ліцензія: CC BY-SA: Із Зазначенням Авторства
Теплове розширення. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Thermal_Expansion. Ліцензія: CC BY: Зазначення авторства
Теплове розширення. Знаходиться за адресою: http://www.youtube.com/watch?v=3P7gHzpXpmU. Ліцензія: Суспільне надбання: Немає відомих авторських прав. Умови ліцензії: Стандартна ліцензія YouTube
Безмежний. Надається: Веб-сервіси Amazon. Розташований за адресою: s3.amazonaws.com/figures.boundless.com/510d56c6e4b0c14bf464b1af/1.jpg. Ліцензія: CC BY: Зазначення авторства
Теплове розширення. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Thermal_розширення%23area_розширення. Ліцензія: CC BY-SA: Із Зазначенням Авторства
коефіцієнт лінійного теплового розширення. Надано: Вікіпедія. Розташований за адресою: en.wikipedia.org/Wiki/Linear% 20 Теплове %20 Коефіцієнт розширення%20. Ліцензія: CC BY-SA: Із Зазначенням Авторства
Теплове розширення. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Thermal_Expansion. Ліцензія: CC BY: Зазначення авторства
Теплове розширення. Знаходиться за адресою: http://www.youtube.com/watch?v=3P7gHzpXpmU. Ліцензія: Суспільне надбання: Немає відомих авторських прав. Умови ліцензії: Стандартна ліцензія YouTube
Безмежний. Надається: Веб-сервіси Amazon. Розташований за адресою: s3.amazonaws.com/figures.boundless.com/510d56c6e4b0c14bf464b1af/1.jpg. Ліцензія: CC BY: Зазначення авторства
OpenStax College, Теплове розширення твердих тіл і рідин. 2 лютого 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42215/latest/. Ліцензія: CC BY: Зазначення авторства
Теплове розширення. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Thermal_Expansion. Ліцензія: CC BY-SA: Із Зазначенням Авторства
коефіцієнт лінійного теплового розширення. Надано: Вікіпедія. Розташований за адресою: en.wikipedia.org/Wiki/Linear% 20 Теплове %20 Коефіцієнт розширення%20. Ліцензія: CC BY-SA: Із Зазначенням Авторства
ізотропний. Надано: Вікісловник. Розташований за адресою: uk.wiktionary.org/wiki/ізотропний. Ліцензія: CC BY-SA: Із Зазначенням Авторства
Теплове розширення. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Thermal_Expansion. Ліцензія: CC BY: Зазначення авторства
Теплове розширення. Знаходиться за адресою: http://www.youtube.com/watch?v=3P7gHzpXpmU. Ліцензія: Суспільне надбання: Немає відомих авторських прав. Умови ліцензії: Стандартна ліцензія YouTube
Безмежний. Надається: Веб-сервіси Amazon. Розташований за адресою: s3.amazonaws.com/figures.boundless.com/510d56c6e4b0c14bf464b1af/1.jpg. Ліцензія: CC BY: Зазначення авторства
OpenStax College, Теплове розширення твердих тіл і рідин. 2 лютого 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42215/latest/. Ліцензія: CC BY: Зазначення авторства
Теплове розширення - розширення обсягу. Знаходиться за адресою: http://www.youtube.com/watch?v=3P7gHzpXpmU. Ліцензія: Суспільне надбання: Немає відомих авторських прав. Умови ліцензії: Стандартна ліцензія YouTube
OpenStax College, Теплове розширення твердих тіл і рідин. 2 лютого 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42215/latest/. Ліцензія: CC BY: Зазначення авторства
OpenStax College, Теплове розширення твердих тіл і рідин. 17 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42215/latest/. Ліцензія: CC BY: Зазначення авторства
Властивості води. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Властивості_оф_вода. Ліцензія: CC BY-SA: Із Зазначенням Авторства
водневий зв'язок. Надано: Вікісловник. Розташований за адресою: uk.wiktionary.org/wiki/hydrogen_bond. Ліцензія: CC BY-SA: Із Зазначенням Авторства
Теплове розширення. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Thermal_Expansion. Ліцензія: CC BY: Зазначення авторства
Теплове розширення. Знаходиться за адресою: http://www.youtube.com/watch?v=3P7gHzpXpmU. Ліцензія: Суспільне надбання: Немає відомих авторських прав. Умови ліцензії: Стандартна ліцензія YouTube
Безмежний. Надається: Веб-сервіси Amazon. Розташований за адресою: s3.amazonaws.com/figures.boundless.com/510d56c6e4b0c14bf464b1af/1.jpg. Ліцензія: CC BY: Зазначення авторства
OpenStax College, Теплове розширення твердих тіл і рідин. 2 лютого 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42215/latest/. Ліцензія: CC BY: Зазначення авторства
Теплове розширення - розширення обсягу. Знаходиться за адресою: http://www.youtube.com/watch?v=3P7gHzpXpmU. Ліцензія: Суспільне надбання: Немає відомих авторських прав. Умови ліцензії: Стандартна ліцензія YouTube
OpenStax College, Теплове розширення твердих тіл і рідин. 2 лютого 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42215/latest/. Ліцензія: CC BY: Зазначення авторства
Властивості води. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Властивості_оф_вода. Ліцензія: CC BY: Зазначення авторства
OpenStax College, Теплове розширення твердих тіл і рідин. 2 лютого 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42215/latest/. Ліцензія: CC BY: Зазначення авторства