10.6: Деформація твердих тіл

Last updated
Save as PDF

Page ID: 75124

Boundless
Boundless

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Поясніть, як визначається довжина об'єкта

Довжина

У геометричних вимірах довжина - це найдовший розмір об'єкта. В інших контекстах «довжина» - це виміряний розмір об'єкта. Наприклад: можна відрізати довжину дроту, яка коротша за товщину дроту. Довжину можна відрізнити від висоти, яка є вертикальною протяжністю, і шириною або шириною, які є відстанню з боку в бік, вимірюючи поперек об'єкта під прямим кутом до довжини.

Довжина - це міра одного виміру, тоді як площа - це міра двох вимірів (довжина в квадраті), а об'єм - міра трьох вимірів (довжина в кубі). У більшості систем вимірювання одиниця довжини - це фундаментальна одиниця, з якої визначаються інші одиниці.

Після спеціальної теорії відносності Альберта Ейнштейна довжина більше не може вважатися постійною у всіх еталонних системах. Таким чином, лінійка довжиною в один метр в одному кадрі відліку не буде довжиною один метр у відліковому кадрі, який рухається зі швидкістю відносно першого кадру. Це означає, що довжина об'єкта є змінною в залежності від спостерігача.

Одиниці

Однією з найстаріших одиниць вимірювання довжини, використовуваних у стародавньому світі, був «лікоть», який був довжиною руки від кінчика пальця до ліктя. Потім це можна поділити на більш короткі одиниці, такі як стопа, рука (яка на 4 дюйми все ще використовується сьогодні для вираження висоти коней) або палець, або додати разом, щоб зробити довші одиниці, як крок. Лікоть міг значно відрізнятися через різні розміри людей.

У фізичних науках та техніці, коли говорять про «одиниці довжини», слово «довжина» є синонімом «відстань». Існує кілька одиниць, які використовуються для вимірювання довжини. Одиниці довжини можуть базуватися на довжині частин тіла людини, відстані, пройденої в ряді кроків, відстані між орієнтирами або місцями на Землі, або довільно на довжині якогось нерухомого об'єкта.У Міжнародній системі одиниць (СІ) основною одиницею довжини є метр і тепер визначається в терміни швидкості світла. Сантиметр і кілометр, отримані від метра, також зазвичай використовуються одиниці. У США звичні одиниці, англійська або імперська система одиниць, зазвичай використовуються одиниці довжини дюйм, фут, двір, і миля. Одиниці, що використовуються для позначення відстаней на просторах космосу, як і в астрономії, набагато довші, ніж ті, які зазвичай використовуються на Землі, і включають астрономічну одиницю, світловий рік і парсек.

зображення

Довжина: метрична довжина одного кілометра еквівалентна імперському виміру 0.62137 миль.

Форма

Форма предмета - це опис простору, який займає об'єкт; форма може змінюватися, якщо об'єкт деформується.

навчальні цілі

Опишіть наслідки деформацій, обертань і збільшень

Форма

Форма об'єкта, розташованого в деякому просторі, є геометричним описом частини простору, зайнятої об'єктом, що визначається його зовнішньою межею — абстрагуванням від місця розташування та орієнтації в просторі, розміру та інших властивостей, таких як колір, зміст та склад матеріалу

Прості та складні форми

Прості форми можуть бути описані основними об'єктами геометрії, такими як набір з двох або більше точок, лінія, крива, площина, плоска фігура (наприклад, квадрат або коло) або суцільна фігура (наприклад, куб або сфера). Більшість форм, що відбуваються у фізичному світі, є складними. Деякі, такі як рослинні структури та берегові лінії, можуть бути настільки довільними, щоб кинути виклик традиційному математичному опису - і в цьому випадку вони можуть бути проаналізовані за допомогою диференціальної геометрії або як фрактали.

У геометрії дві підмножини евклідового простору мають однакову форму, якщо одна може бути перетворена в іншу комбінацією перекладів, обертань (разом також званих жорсткими перетвореннями) та рівномірних масштабів. Іншими словами, форма множини точок - це вся геометрична інформація, яка є неваріантною до перекладів, поворотів і змін розмірів. Така ж форма є співвідношенням еквівалентності, і відповідно точне математичне визначення поняття форми може бути дано як клас еквівалентності підмножин евклідового простору, що має однакову форму.

Форми фізичних об'єктів рівні, якщо підмножини простору, які займають ці об'єкти, задовольняють визначенню вище. Зокрема, форма не залежить від розмірів і розміщення в просторі об'єкта.

зображення

Фігури: приклади фігур.

Обсяг

Об'єм - це міра тривимірного простору, який займає об'єкт, зазвичай приймається з точки зору довжини, ширини та висоти.

навчальні цілі

Поясніть, як вимірюється об'єм геометрично

Об'єм - це кількість тривимірного простору, що міститься замкнутою межею; це простір, який займає або містить речовина (тверда, рідина, газ або плазма) або форма. Обсяг часто кількісно визначається чисельно, використовуючи одиницю, похідну SI, кубічний метр. Однак для рідин використовувана одиниця об'єму відома як літр (еквівалентно 0,001 кубічному метру).

зображення

Вимірювальний об'єм: мірну чашку можна використовувати для вимірювання обсягів рідин. Ця чашка вимірює об'єм в одиницях чашок, рідких унцій і мілілітрів.

Об'єм вимірюється геометрично шляхом множення трьох вимірів об'єкта - зазвичай приймається як довжина, ширина та висота. Деякі загальні обсяги приймаються наступним чином:

Об'єм куба: довжина на ширину на висоту.
Обсяг циліндра: площа поперечного перерізу на висоту циліндра.
Обсяг сфери: 4/3 радіус в кубі разів pi.

Обсяг твердої речовини можна визначити за обсягом рідини, яку воно витісняє при зануренні.

Обсяг контейнера, як правило, розуміється як ємність контейнера, тобто кількість рідини (газу або рідини), яку може вмістити контейнер, а не кількість простору, який сам контейнер витісняє. Вимірювальні чашки, як видно в, працюють, приймаючи відому площу поперечного перерізу чашки і множивши її на змінну висоту. Так як рідина завжди буде покривати поперечний переріз (якщо рідини достатньо), додавання більшої кількості рідини збільшить висоту всередині ємності.

Рідини приймають форму своєї ємності, заповнюючи мінімальну необхідну висоту. Гази, з іншого боку, займають максимальну кількість можливого обсягу. Таким чином мірний стаканчик може точно виміряти обсяг рідини, тоді як газ завжди буде заповнювати всю ємність, більш-менш рівномірно, незалежно від того, наскільки мало газу там.

Стрес і напруга

Точковий заряд створює електричне поле, яке можна обчислити за Законом Кулона.

Електричне поле точкового заряду - це, як і будь-яке електричне поле, векторне поле, яке представляє вплив точкового заряду на інші заряди навколо нього. Ефект відчувається як сила, і коли заряджені частинки не знаходяться в русі, ця сила відома як електростатична сила. Електростатична сила - це, як і гравітація, сила, яка діє на відстані. Тому ми раціоналізуємо цю дію на відстані, кажучи, що заряди створюють навколо них поля, які впливають на інші заряди.

З огляду на точковий заряд, або частинку нескінченно малих розмірів, яка містить певний заряд, лінії електричного поля виходять радіально у всіх напрямках. Якщо заряд позитивний, лінії поля спрямовані радіально від нього; якщо заряд негативний, лінії поля спрямовані радіально до нього.

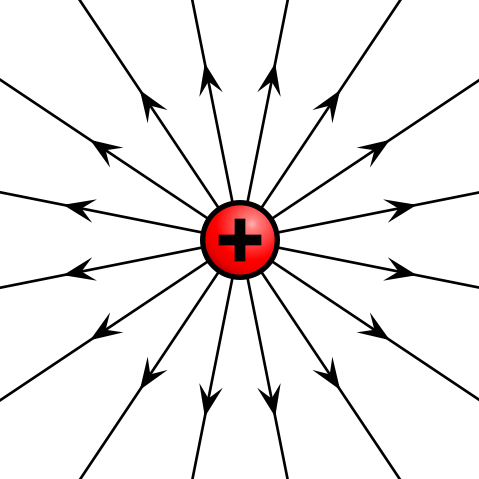
зображення

Електричне поле позитивного точкового заряду: Електричне поле позитивно зарядженої частинки вказує радіально від заряду.

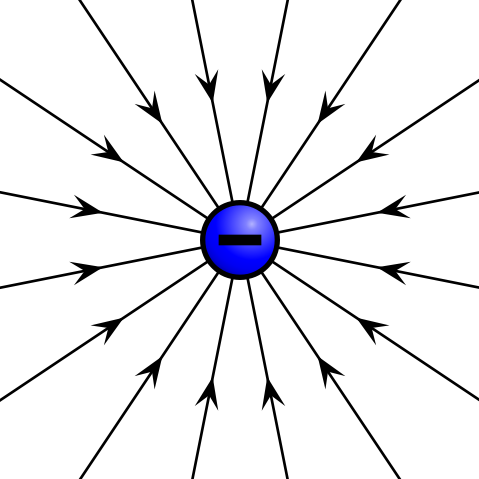
зображення

Електричне поле негативного точкового заряду: Електричне поле негативно зарядженої частинки вказує радіально до частинки.

Причину цих напрямків можна побачити в виведенні електричного поля точкового заряду. Давайте спочатку розберемося з визначенням електричного поля точкової частинки:

\[\mathrm{\overrightarrow{E}=\dfrac{1}{4πϵ_o}\dfrac{q}{r^2} \hat{r}=k\dfrac{q}{r^2} \hat{r}.}\]

У наведеному вище рівнянні q представляє заряд частинки, що створює електричне поле, а постійна k є результатом простого об'єднання констант разом. Цей заряд буває або позитивним, або негативним. Якщо заряд позитивний, як показано вище, електричне поле буде спрямоване в позитивному радіальному напрямку від заряду q (подалі від заряду) і наступний текст пояснює, чому. Вищевказане рівняння визначається в радіальних координатах, які можна побачити в.

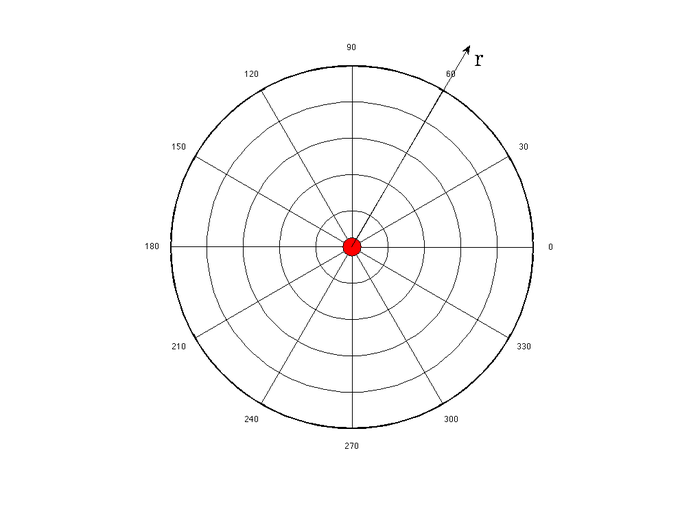
зображення

Радіальна система координат: Електричне поле точкового заряду визначається в радіальних координатах. Позитивний напрямок r вказує від початку, а негативний напрямок r вказує на початок. Електричне поле точкового заряду симетрично щодо напрямку θ.

Якщо ми зараз розмістимо інший позитивний заряд, Q (званий тестовим зарядом), на деякій радіальній відстані, R, далеко від вихідної частинки, випробувальний заряд відчує силу, задану

\[\mathrm{\overrightarrow{F}=Q\overrightarrow{E}=Q\dfrac{1}{4πϵ_o}\dfrac{q}{R^2}\hat{r}}\]

Слід пам'ятати, що сила вище діє на тестовий заряд Q, в позитивному радіальному напрямку, визначеному початковим зарядом q Це означає, що оскільки заряди обидва позитивні і будуть відштовхувати один одного, сила на тестовому заряді вказує подалі від початкового заряду.

Якби тестовий заряд був негативним, сила, що відчувається на цьому заряді, була б

\[\mathrm{\overrightarrow{F}=Q\overrightarrow{E}=-Q\dfrac{1}{4πϵ_o}\dfrac{q}{R^2}\hat{r}}\]

Зверніть увагу, що це вказує в негативну\(\mathrm{\hat{r}}\) сторону, яка знаходиться в бік початкового заряду. Це має сенс, оскільки протилежні заряди притягуються, і сила на тестовому заряді, як правило, підштовхує його до початкового позитивного заряду, створюючи поле. Наведений вище математичний опис електричного поля точкового заряду відомий як Закон Кулона.

Ключові моменти

Довжина, як правило, є мірою найдовшого розміру об'єкта.
Деформація об'єкта - це, як правило, зміна довжини.
Одиницею довжини СІ є метр.
Форма предмета - це подання простору, зайнятого об'єктом.
Деформації можуть змінювати форму предмета.
Об'єкти, які мають однакову форму, можуть трансформуватися один в одного обертанням або збільшенням.
Обсяг часто кількісно визначається чисельно, використовуючи одиницю, похідну SI, кубічний метр. Однак для рідин використовувана одиниця об'єму відома як літр (еквівалентно 0,001 кубічному метру).
Це також можна розуміти як кількість рідини, яку витісняє занурений об'єкт.
Обсяг можна виміряти для геометрично правильних об'єктів за простими формулами. Однак більш складні об'єкти легше вимірювати при витісненні рідини.
Електричне поле - це векторне поле навколо зарядженої частинки, яке представляє силу, яку відчували б інші заряджені частинки при розміщенні поблизу частинки, що створює електричне поле.
З огляду на точковий заряд, або частинку нескінченно малих розмірів, що містить певний заряд, лінії електричного поля виходять однаково у всіх радіальних напрямках.
Якщо точковий заряд позитивний, лінії полів вказують від нього; якщо заряд негативний, лінії полів вказують на нього.

Ключові умови

вимір: міра просторової протяжності в певному напрямку, наприклад, висота, ширина або ширина або глибина.
спеціальна теорія відносності: теорія, яка (нехтуючи ефектами гравітації) узгоджує принцип відносності із спостереженням про те, що швидкість світла постійна у всіх системах відліку.
площина: Рівна або рівна поверхня.
Евклідів: Дотримуючись принципів традиційної геометрії, в якій паралельні лінії рівновіддалені.
поперечний переріз: переріз, утворений площиною, що прорізається через об'єкт, зазвичай під прямим кутом до осі.
вимір: міра просторової протяжності в певному напрямку, наприклад, висота, ширина або ширина або глибина.
закон Кулона: математичне рівняння, що обчислює вектор електростатичної сили між двома зарядженими частинками
векторне поле: конструкція, в якій кожна точка евклідового простору пов'язана з вектором; функція, діапазон якої є векторним простором