Skip to main content
LibreTexts - Ukrayinska

10.3: Принцип Архімеда

  1. Last updated
  2. Save as PDF
  • Page ID
    75136

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    цілі навчання

    • Обчисліть напрямок сили плавучості

    Коли ви піднімаєтеся від замочування в теплій ванні, ваші руки можуть відчувати себе дивно важкими. Такий ефект обумовлений втратою плавучої опори води. Що створює ця плавуча сила? Чому одні речі плавають, а інші ні? Чи отримують предмети, які тонуть, взагалі будь-яку опору від рідини? Ваше тіло підживлюється атмосферою, чи впливають лише гелієві кулі?

    Плавуча сила: причина і розрахунок

    Відповіді на перераховані вище питання знаходимо в тому, що в будь-якій даній рідини тиск збільшується з глибиною. Коли об'єкт занурений у рідину, висхідна сила на дні об'єкта більша, ніж сила вниз на верхній частині об'єкта. Результатом є чиста висхідна сила (плавуча сила) на будь-якому об'єкті в будь-якій рідині. Якщо плавуча сила більша за вагу об'єкта, об'єкт підніметься на поверхню і попливе. Якщо плавуча сила менше ваги об'єкта, об'єкт потоне. Якщо плавуча сила дорівнює вазі об'єкта, об'єкт залишатиметься підвішеним на цій глибині. Плавуча сила завжди присутня в рідині, незалежно від того, чи предмет плаває, тоне або залишається підвішеним.

    Плавуча сила є результатом тиску, що чиниться рідиною. Рідина штовхає з усіх боків зануреного предмета, але зі збільшенням тиску з глибиною поштовх сильніший на нижній поверхні об'єкта, ніж у верхній (як видно з).

    Ви можете обчислити плавучу силу на об'єкті, склавши сили, що чинилися з усіх сторін об'єкта. Наприклад, розглянемо об'єкт, показаний в.

    Верхня поверхня має площу\(\mathrm{A}\) і знаходиться на глибині\(\mathrm{h_1}\); тиск на цій глибині становить:

    \[\mathrm{P_1=h_1ρg,}\]

    де ρ - щільність рідини і\(\mathrm{g≈9.81 \frac{m}{s^2}}\) - гравітаційне прискорення. Величина сили на верхній поверхні дорівнює:

    \[\mathrm{F_1=P_1A=h_1ρgA.}\]

    Ця сила вказує вниз. Аналогічно сила на нижній поверхні становить:

    \[\mathrm{F_2=P_2A=h_2ρgA}\]

    і вказує вгору. Оскільки вона циліндрична, чиста сила з боків об'єкта дорівнює нулю - сили на різних ділянках поверхні протистоять один одному і скасовуються точно. Таким чином, чиста висхідна сила на циліндрі за рахунок рідини становить:

    \[\mathrm{F_B=F_2−F_1=ρgA(h_2−h_1)}\]

    Принцип Архімеда

    Хоча розрахувати плавучу силу таким способом завжди можливо, часто буває дуже складно. Простіший метод випливає з принципу Архімеда, який стверджує, що плавуча сила, що чиниться на тіло, занурене в рідину, дорівнює вазі рідини, яку витісняє організм. Іншими словами, для обчислення плавучої сили на об'єкт ми припускаємо, що занурена частина об'єкта зроблена з води, а потім обчислюємо вагу цієї води (як видно з).

    зображення

    Принцип Архімеда: Плавуча сила на кораблі (а) дорівнює вазі води, витісненої кораблем - показана як пунктирна область в (b).

    Принцип можна викласти у вигляді формули:

    \[\mathrm{F_B=w_{fl}}\]

    Міркування принципу Архімеда полягає в тому, що сила плавучості на предмет залежить від тиску, який чинить рідина на його занурену поверхню. Уявімо, що ми замінюємо занурену частину об'єкта рідиною, в якій він міститься, як в (б). Сила плавучості на цю кількість рідини повинна бути такою ж, як і на вихідному об'єкті (кораблі). Однак ми також знаємо, що сила плавучості на рідину повинна дорівнювати її вазі, оскільки рідина не тоне сама по собі. Тому сила плавучості на вихідному об'єкті дорівнює вазі «витісненої рідини» (в даному випадку вода всередині пунктирної області (б)).

    Принцип Архімеда діє для будь-якої рідини - не тільки рідин (наприклад, води), але й газів (наприклад, повітря). Ми будемо вивчати це далі, коли ми обговорюємо застосування принципу в наступних розділах.

    Принцип Архімеда - Простий приклад: Ми використовуємо принцип Архімеда для визначення кількості пінгвінів, яких крижаний поплавок може сухо підтримувати.

    Повне занурення

    Сила плавучості на повністю зануреному об'єкті об'єму становить\(\mathrm{F_B=Vρg}\).

    навчальні об'єктивності

    • Визначити фактори, що визначають силу плавучості на повністю зануреному об'єкті

    Принцип Архімеда найпростіше зрозуміти і застосувати в разі повністю занурених об'єктів. У цьому розділі ми розглянемо кілька відповідних прикладів. В цілому сила плавучості на повністю зануреному об'єкті задається за формулою:

    \[\mathrm{F_B=Vρg,}\]

    де\(\mathrm{V}\) - обсяг об'єкта,\(\mathrm{ρ}\) - щільність рідини, а\(\mathrm{g}\) також гравітаційне прискорення. Це випливає відразу з принципу Архімеда, і того, що об'єкт повністю занурений (а тому обсяг рідини, що витісняється, - це всього лише обсяг об'єкта).

    Циліндр

    У попередньому розділі ми розрахували силу плавучості на циліндрі (показано на), враховуючи силу, що чиниться на кожній зі сторін циліндра. Тепер ми розрахуємо цю силу за принципом Архімеда. Сила плавучості на циліндрі дорівнює вазі витісняється рідини. Ця вага дорівнює масі витісненої рідини, помноженої на прискорення гравітації:

    зображення

    Плавуча сила: рідина штовхає з усіх боків зануреного об'єкта. Однак, оскільки тиск збільшується з глибиною, висхідний поштовх на нижній поверхні (F2) більший, ніж натискання вниз на верхній поверхні (F1). Тому чиста плавуча сила завжди вгору.

    \[\mathrm{F_B=w_{fl}=m_{fl}g}\]

    Маса витісняється рідини дорівнює її об'єму, помноженому на її щільність:

    \[\mathrm{m_{fl}=V_{fl}ρ}\]

    Однак (а це найважливіший момент) циліндр повністю занурений, тому обсяг витісняється рідини - це якраз обсяг циліндра (див.), а:

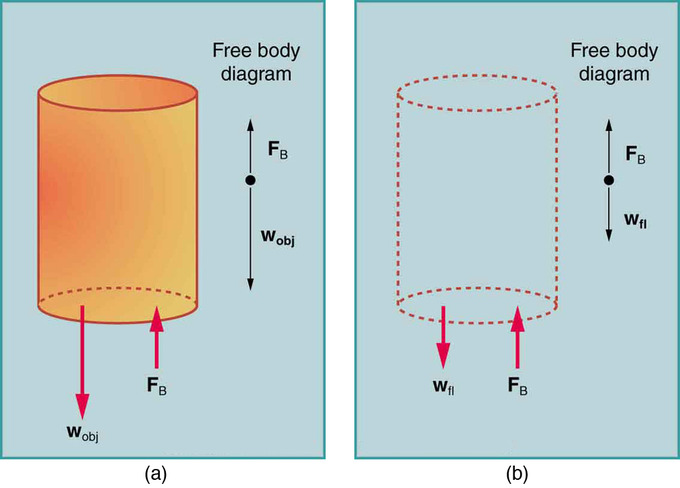
    зображення

    Принцип Архімеда: Обсяг рідини, що витісняється (b), такий же, як і обсяг вихідного циліндра (а).

    \[\mathrm{m_{fl}=V_{fl}ρ=V_{cylinder}ρ.}\]

    Обсяг циліндра - це площа його підстави, помножена на його висоту, або в нашому випадку:

    \[\mathrm{V_{cylinder}=A(h_2−h_1).}\]

    Тому сила плавучості на циліндрі становить:

    \[\mathrm{F_B=m_{fl}g=V_{cylinder}ρg=(h_1−h_2)ρgA.}\]

    Це той самий результат, отриманий в попередньому розділі, враховуючи силу, обумовлену тиском, що чиниться рідиною.

    Гелій дирижабль

    Розглянемо USS Macon, наповнений гелієм дирижабль (показано на). Його оболонка («повітряна куля») містила 184059,5 кубометрів гелію. Ігноруючи малий обсяг гондоли, яка була сила плавучості на цьому дирижаблі? Якби дирижабль важив 108 000 кг, скільки вантажу він міг би перевезти? Припустимо, щільність повітря становить 1,225 кг на метр в кубі. Сила плавучості на дирижаблі обумовлена повітрям, в який він занурений. Хоча ми не знаємо точної форми дирижабля, ми знаємо його обсяг і щільність повітря, і таким чином ми можемо обчислити силу плавучості:

    зображення

    Гелій дирижабль: USS Macon, 1930-х років, наповнений гелієм дирижабль.

    \[\mathrm{F_B=V_{ρg}=184,059.5 \; kg \times 1.225 \dfrac{kg}{m^3} \times 9.81 \dfrac{m}{s^2}≈2.212 \times 10^6 \; N}\]

    Щоб знайти вантажопідйомність дирижабля, віднімаємо вагу дирижабля з сили плавучості:

    \[\mathrm{F_{cargo}=F_B−mg=2.21 \times 10^6 \; N−1.08 \times 10^5 \; kg \times 9.81 \dfrac{m}{s^2}=1.15 \times 10^6 \; N}\]

    Маса, яку може нести дирижабль, становить:

    \[\mathrm{m_{cargo}=\dfrac{F_{cargo}}{g}=1.2 \times 10^5 \; kg= 120 \; tons.}\]

    Флотація

    Об'єкт плаває, якщо сила плавучості, що чиниться на нього рідиною, врівноважує свою вагу.

    цілі навчання

    • Висловіть зв'язок між силою плавучості та вагою для плавучого об'єкта

    Чому одні об'єкти плавають, а інші ні? Якщо покласти металеву монету в склянку з водою, вона буде тонути. Але більшість кораблів побудовані з металу, і вони плавають. Так як же це можливо?

    Умова для флотації

    Об'єкт буде плавати, якщо сила плавучості, що чиниться на нього рідиною, врівноважує свою вагу, тобто якщо FB = mgFb=mg.

    Але принцип Архімеда стверджує, що плавуча сила - це вага витісненої рідини. Так, для плаваючого об'єкта на рідині вага витісняється рідини - це вага предмета. Таким чином, тільки в особливому випадку плаваючого робить плавуча сила, що діє на об'єкт, рівну вазі об'єкта. Розглянемо однотонний блок з твердого заліза. Оскільки залізо майже у вісім разів щільніше води, воно витісняє лише 1/8 тонни води при зануренні, що недостатньо, щоб утримати його на плаву. Припустимо, той же залізний блок переформується в чашу. Він все ще важить одну тонну, але коли його кладуть у воду, він витісняє більший об'єм води, ніж коли це був блок. Чим глибше занурена залізна чаша, тим більше води вона витісняє, і тим більше діє на неї плавуча сила. Коли плавуча сила дорівнює одній тонні, вона не буде просідати далі.

    Коли будь-який човен витісняє вагу води, рівну власній вазі, вона плаває. Це часто називають «принципом флотації», коли плаваючий об'єкт витісняє вагу рідини, рівну його власній вазі. Кожен корабель, підводний човен та дирижабль повинні бути спроектовані таким чином, щоб витіснити вагу рідини, рівну його власній вазі. 10000-тонний корабель повинен бути побудований досить широким, щоб витіснити 10 000 тонн води, перш ніж він зануриться занадто глибоко у воду. Те саме стосується суден у повітрі (оскільки повітря - це рідина): дирижабль, який важить 100 тонн, витісняє щонайменше 100 тонн повітря; якщо він витісняє більше, він піднімається; якщо він витісняє менше, падає. Якщо дирижабль зміщує саме свою вагу, він ширяє на постійній висоті.

    Флотація і щільність

    Щільність відіграє вирішальну роль у принципі Архімеда. Середня щільність об'єкта - це те, що в кінцевому підсумку визначає, чи плаває він. Якщо його середня щільність буде менше, ніж у навколишньої рідини, вона буде плавати. Це пояснюється тим, що рідина, маючи більш високу щільність, містить більше маси і, отже, більше ваги в тому ж обсязі. Плавуча сила, яка дорівнює вазі зміщеної рідини, таким чином, більша за вагу предмета. Так само буде занурюватися предмет, щільніший за рідину. Ступінь занурення плаваючого об'єкта залежить від того, як щільність об'єкта пов'язана з щільністю рідини. Наприклад, ненавантажене судно має меншу щільність, і менша його частина занурюється в воду в порівнянні з тим же судном, завантаженим вантажем. Ми можемо отримати кількісний вираз для фракції, зануреної в воду, враховуючи щільність. Фракція занурена - це відношення обсягу зануреного до обсягу об'єкта, або

    зображення

    Щільність і занурення: Незавантажений корабель (а) плаває вище у воді, ніж завантажене судно (б).

    \[\mathrm{fraction \; submerged=\dfrac{V_{sub}}{V_{obj}}=\dfrac{V_{fl}}{V_{obj}}}\]

    Обсяг зануреного дорівнює об'єму витісненої рідини, який ми називаємо\(\mathrm{V_{fl}}\). Тепер ми можемо отримати зв'язок між щільностями шляхом підстановки\(\mathrm{ρ=mV}\) в вираз. Це дає

    \[\mathrm{fraction \; submerged=\dfrac{m_{fl}/ρ_{fl}}{m_{obj}/ \bar{ρ}_{obj}}}\]

    де\(\mathrm{\bar{ρ}_{obj}}\) - середня щільність предмета і ρ flρflis щільність рідини. Оскільки об'єкт плаває, його маса та маса витісненої рідини рівні, і тому вони скасовуються з рівняння, залишаючи

    \[\mathrm{fraction \; submerged=\dfrac{\bar{ρ}_{obj}}{ρ_{fl}.}}\]

    Є кілька речей, які слід зазначити щодо цього виразу:

    1. Зверніть увагу, що в ньому згадується середня щільність об'єкта. Це може бути набагато менше щільності матеріалу, з якого виготовлений предмет. Наприклад, сталевий корабель насправді в основному заповнений повітрям (подумайте про коридори, вантажні трюми тощо), тому його середня щільність знаходиться між щільністю повітря та сталі. Якщо бути точніше, то середня щільність визначається як загальна маса предмета, поділена на його загальний обсяг:\(\mathrm{\bar{ρ}=\frac{m}{V}.}\)
    2. Ця формула має сенс тільки в тому випадку, якщо щільність предмета менше щільності рідини. Інакше занурена фракція стає більшою за одиницю — ознака того, що об'єкт взагалі не плаває, а тоне!

    Ключові моменти

    • Сила плавучості викликана тиском, що чиниться рідиною, в яку занурений предмет.
    • Сила плавучості завжди вказує вгору, оскільки тиск рідини збільшується з глибиною.
    • Розрахувати силу плавучості можна або безпосередньо шляхом обчислення сили, що чиниться на кожній з поверхонь об'єкта, або опосередковано шляхом знаходження ваги витісненої рідини.
    • Якщо об'єкт повністю занурений, обсяг рідини, що витісняється, дорівнює об'єму предмета.
    • Силу плавучості на повітряні кулі, дирижаблі та інші об'єкти можна розрахувати, припускаючи, що вони повністю занурені в повітря.
    • Сила плавучості залежить не від форми предмета, тільки від його обсягу.
    • Сила плавучості, яку відчуває об'єкт, залежить від його форми.
    • Частка об'єму об'єкта, що занурюється, визначається співвідношенням його середньої щільності до щільності рідини:\(\mathrm{\frac{\bar{ρ}_{obj}}{ρ_{fl}}}\).
    • Об'єкт плаває, якщо сила плавучості, що чиниться на нього рідиною, врівноважує свою вагу.

    Ключові умови

    • плавуча сила: висхідна сила, що чиниться рідиною, яка протистоїть вазі зануреного предмета.
    • Принцип Архімеда: Плавуча сила, що чиниться на тіло, занурене в рідину, дорівнює вазі рідини, яку тіло витісняє.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ