Skip to main content
LibreTexts - Ukrayinska

1.4: Розв'язування задач фізики

  1. Last updated
  2. Save as PDF
  • Page ID
    75254

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розмірний аналіз

    Будь-яка фізична величина може бути виражена як добуток комбінації основних фізичних вимірів.

    навчальні цілі

    • Обчисліть перетворення з одного виду вимірності в інший

    Розміри

    Розмірність фізичної величини вказує на те, як вона відноситься до однієї з семи основних величин. Цими основними величинами є:

    • [М] Маса
    • [L] Довжина
    • [T] Час
    • [A] Струм
    • [K] Температура
    • [моль] Кількість речовини
    • [cd] Інтенсивність світла

    Як бачите, символ укладений в пару квадратних дужок. Це часто використовується для представлення виміру індивідуальної основної кількості. Прикладом використання основних розмірів є швидкість, яка має розмірність 1 в довжину і -1 в часі;\(\mathrm{\frac{[L]}{[T]}=[LT^{−1}]}\). Будь-яка фізична величина може бути виражена як добуток комбінації основних фізичних вимірів.

    Розмірний аналіз

    Розмірний аналіз - це практика перевірки відносин між фізичними величинами шляхом ідентифікації їх розмірів. Розмірність будь-якої фізичної величини - це поєднання основних фізичних вимірів, які її складають. Розмірний аналіз заснований на тому, що фізичний закон повинен бути незалежним від одиниць, що використовуються для вимірювання фізичних змінних. Він може бути використаний для перевірки правдоподібності похідних рівнянь, обчислень і гіпотез.

    похідні розміри

    Розміри похідних величин можуть включати кілька або всі розміри в окремих основних кількостях. Для того щоб зрозуміти техніку написання розмірів похідної величини, розглянемо випадок сили. Сила визначається як:

    \[\begin{align} \mathrm{F} &= \mathrm{m⋅a} \\ \mathrm{F} &= \mathrm{[M][a]} \end{align}\]

    Розмірність прискорення, представлена як [a], сама по собі є похідною величиною, яка є співвідношенням швидкості та часу. У свою чергу, швидкість - це також похідна величина, яка є співвідношенням довжини і часу.

    \[\begin{align} \mathrm{F} &= \mathrm{[M][a]=[M][vT^{−1}]} \\ \mathrm{F} &= \mathrm{[M][LT^{−1}T^{−1}]=[MLT^{−2}]} \end{align}\]

    Розмірне перетворення

    На практиці може знадобитися перетворення з одного виду виміру в інший. Для звичайних перетворень ви, можливо, вже знаєте, як конвертувати верхню частину голови. Але для менш поширених корисно знати, як знайти коефіцієнт перетворення:

    \[\mathrm{Q=n_1u_1=n_2u_2}\]

    де n являє собою величину за u розмірами. Потім ви можете використовувати коефіцієнти, щоб з'ясувати конверсію:

    \[\mathrm{n_2=\dfrac{u_2}{u_1}⋅n_1}\]

    Тригонометрія

    Тригонометрія займає центральне місце у використанні діаграм вільного тіла, які допомагають візуально представляти складні проблеми фізики.

    навчальні цілі

    • Поясніть, чому тригонометрія корисна при визначенні горизонтальної та вертикальної складових сил

    Тригонометрія та розв'язання задач фізики

    У фізиці більшість завдань вирішуються набагато легше, коли використовується діаграма вільного тіла. Вільні діаграми тіла використовують геометрію та вектори для візуального представлення проблеми. Тригонометрія використовується також при визначенні горизонтальної і вертикальної складових сил і предметів. Вільні діаграми тіла дуже корисні для візуального визначення того, які компоненти невідомі і де моменти застосовуються. Вони можуть допомогти проаналізувати проблему, будь то статична або динамічна.

    Коли люди малюють вільні схеми тіла, часто не все ідеально паралельно і перпендикулярно. Іноді людям потрібно аналізувати горизонтальну і вертикальну складові сил і орієнтацію об'єкта. Коли сила або об'єкт не діють паралельно осі x або y, люди можуть використовувати базову тригонометрію, щоб використовувати найпростіші компоненти дії для її аналізу. В основному все слід розглядати з точки зору x і y, що іноді вимагає певних маніпуляцій.

    fbd10a.gif

    Діаграма вільного тіла: Стрижень шарнірно відкидається від стіни і утримується за допомогою струни.

    Стрижень 'AB' шарнірно на 'A' від стіни і утримується нерухомо за допомогою струни, як показано в. Ця вправа передбачає складання схеми вільного тіла. Щоб полегшити завдання, сила F буде виражена в плані її горизонтальної і вертикальної складових. Видалення всіх інших елементів з зображення допомагає виробляти готову схему вільного тіла.

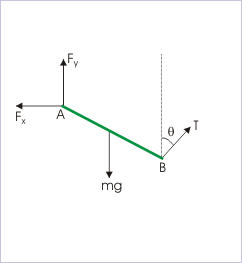
    fbd12a.gif

    Діаграма вільного тіла: вільна діаграма тіла як готовий продукт

    З огляду на готову діаграму вільного тіла, люди можуть використовувати свої знання з тригонометрії та законів синуса і косинуса, щоб математично і числово представляти горизонтальну і вертикальну складові:

    Загальні хитрощі вирішення проблем

    Вільні діаграми тіла використовують геометрію та вектори для візуального представлення проблеми.

    навчальні цілі

    • Побудувати діаграму вільного тіла для фізичного сценарію

    У фізиці більшість завдань вирішуються набагато легше, коли використовується діаграма вільного тіла. Це використовує геометрію та вектори для візуального представлення задачі, а тригонометрія також використовується при визначенні горизонтальних і вертикальних складових сил і об'єктів.

    Мета: Вільні діаграми тіла дуже корисні для візуального визначення того, які компоненти невідомі, де моменти застосовуються, і допомагають проаналізувати проблему, будь то статична чи динамічна.

    Як зробити вільну діаграму тіла

    Щоб намалювати вільну схему тіла, не турбуйтеся про те, щоб намалювати її в масштабі, це буде якраз те, що ви використовуєте, щоб допомогти собі визначити проблеми. Спочатку ви хочете змоделювати тіло одним з трьох способів:

    • Як частинка. Ця модель може бути використана, коли будь-які ефекти повороту дорівнюють нулю або мають нульовий інтерес, навіть якщо сам корпус може бути розширено. Тіло може бути представлено невеликою символічною краплинкою, а діаграма зводиться до набору одночасних стрілок. Сила на частинці - це зв'язаний вектор.
    • жорсткий подовжений. Стреси і деформації не представляють інтересу, але поворотні ефекти є. Силова стрілка повинна лежати уздовж силової лінії, але там, де уздовж лінії, не має значення. Сила на витягнутому жорсткому тілі - це ковзаючий вектор.
    • нежорсткий подовжений. Точка прикладання сили стає вирішальною і має бути вказана на схемі. Сила на нежорсткому тілі - це пов'язаний вектор. Деякі інженери використовують хвостик стрілки для позначення точки застосування. Інші використовують наконечник.

    Робити, а що не потрібно

    Що включати: Оскільки діаграма вільного тіла представляє саме тіло і зовнішні сили на ньому. Таким чином, ви захочете включити наступні речі на діаграмі:

    • Тіло: Зазвичай це намальовано схематично залежно від тіла - частинки/розширеного, жорсткого/нежорсткого - і від того, на які питання потрібно відповісти. Таким чином, якщо враховано обертання корпусу та крутний момент, необхідна вказівка розміру та форми тіла.
    • Зовнішні сили: Вони позначаються маркованими стрілками. У повністю вирішеній задачі силова стрілка здатна вказувати напрямок, величину, точку прикладання. Ці сили можуть бути тертям, гравітацією, нормальною силою, перетягуванням, натягом тощо...

    Не включайте:

    • Не показуйте інші тіла, крім тіла, що цікавить.
    • Чи не показувати сили, що чиниться організмом.
    • Внутрішні сили, що діють на різні частини тіла іншими частинами тіла.
    • Будь-яка швидкість або прискорення залишаються поза увагою.

    Як вирішити будь-яку проблему фізики: Дізнайтеся п'ять простих кроків за п'ять хвилин! У цьому епізоді ми висвітлюємо найефективніший метод вирішення проблем, з яким я зіткнувся, і закликаємо деяких нечітких друзів, щоб допомогти нам запам'ятати кроки.

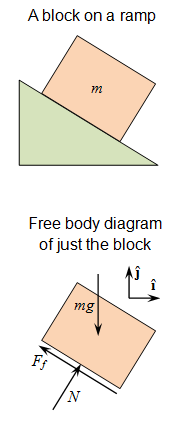
    free-body-diagram.png

    Діаграма вільного тіла: Використовуйте цю фігуру для роботи з прикладом проблеми.

    Ключові моменти

    • Розмірний аналіз - це практика перевірки співвідношень величини фізичних величин шляхом ідентифікації їх розмірів.
    • Зазвичай стикаються з проблемою, яка використовує різні розміри для вираження однієї і тієї ж основної кількості. Для пошуку коефіцієнта перетворення між двома похідними розмірами можна використовувати наступне рівняння:\(\mathrm{n_2=\frac{u_2}{u_1} \times n_1}\).
    • Розмірний аналіз також може бути використаний як проста перевірка обчислень, теорій і гіпотез.
    • Важливо виявити проблему і невідомі і намалювати їх у вільній схемі тіла.
    • Закони косинуса і синуса можна використовувати для визначення вертикальної і горизонтальної складових різних елементів діаграми.
    • Вільні діаграми тіла використовують геометрію та вектори для візуального представлення проблем фізики.
    • Вільна діаграма тіла дозволяє візуально виділити проблему, яку ви намагаєтеся вирішити, і спростити її в простій геометрії та тригонометрії.
    • При складанні цих діаграм корисно лише намалювати тіло саме, і сили, що діють на нього.
    • Малювання інших об'єктів і внутрішніх сил може конденсувати діаграму і викликати її менш корисною.

    Ключові умови

    • вимір: міра просторової протяжності в певному напрямку, наприклад, висота, ширина або ширина або глибина.
    • тригонометрія: галузь математики, яка займається взаємозв'язками між сторонами та кутами трикутників та розрахунками на їх основі, зокрема тригонометричними функціями.
    • статичний: Фіксований на місці; не маючи руху.
    • динамічний: змінюється; активний; в русі.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ