Skip to main content
LibreTexts - Ukrayinska

9.6: Рух кочення

  1. Last updated
  2. Save as PDF
  • Page ID
    74586

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Як крок від статичної задачі ми можемо розглянути ситуацію, в якій сума зовнішніх сил дорівнює нулю, а також сума зовнішніх крутних моментів, але система рухається. Ми називаємо це «непримусовим рухом». Перша умова\(\sum \vec{F}_{e x t}=0 \), означає, що центр маси системи повинен рухатися з постійною швидкістю; друга умова означає, що загальний кутовий імпульс повинен бути постійним. Для жорсткого тіла це означає, що найбільш загальний вид ненасиленого руху можна описати як переклад центру мас з постійною швидкістю, що супроводжується обертанням з постійною кутовою швидкістю навколо центру мас. Для розширеної, деформованої системи, з іншого боку, наявність внутрішніх сил може значно ускладнити загальний рух. Подумайте, наприклад, про Сонячну систему: хоча все, вільно кажучи, обертається навколо Сонця, руху окремих планет і (особливо) супутників можуть бути досить складними.

    Простий приклад (для практичних цілей) невимушеного руху забезпечується симетричним жорстким предметом (таким як куля, або колесо), що котиться по рівній поверхні. Нормальні і гравітаційні сили скасовують один одного, і оскільки вони лежать уздовж однієї лінії, їх крутний момент теж скасовується, тому обидва\(\vec v_{cm}\) і\(\vec L\) залишаються постійними. В принципі, можна було б уявити видалення землі і сили тяжіння і нічого не зміниться: той же рух (при відсутності опору повітря) просто продовжувався б назавжди.

    На практиці відбувається розсіювання енергії, пов'язане з рухом кочення, перш за все тому, що, якщо об'єкт кочення не ідеально жорсткий 6, то, коли він котиться, різні його частини стискаються під спільним тиском сили тяжіння і нормальної сили, знову розширюються, стискаються знову... Цей вид постійного «розгойдування» закінчується перетворенням макроскопічної кінетичної енергії в теплову енергію: ви, можливо, помітили, що шини на автомобілі нагріваються під час їзди, і ви також можете бути знайомі з тим, що ви отримуєте кращий пробіг газу (менше розсіювання енергії), коли ваші шини надуті до правильний тиск, ніж коли вони низькі (тому що вони більш «жорсткі», менш деформуються, в першому випадку).

    Це перетворення механічної енергії в теплову можна формально описати шляхом введення ще однієї сили «тертя», яку ми називаємо силою тертя кочення. Зрештою, лише тертя кочення призведе до зупинки будь-якого предмета кочення, навіть за відсутності опору повітря. Однак це, як правило, набагато слабкіше, ніж тертя ковзання, тому ми будемо продовжувати ігнорувати його відтепер. Можливо, ви вже помітили, що зазвичай об'єкт може котитися по поверхні набагато далі, ніж він може ковзати, не котившись на тій же поверхні. Насправді, часто трапляється те, що, якщо ви спробуєте направити об'єкт (наприклад, більярдну кулю) ковзання, він швидко втратить кінетичну енергію до сили кінетичного тертя, але він також почне обертатися під впливом тієї ж сили, поки не буде досягнута критична точка, коли умова для прокатки без ковзання задовольняється:

    \[ | \vec v_{cm} | = R |\omega| \label{eq:9.34} .\]

    У цей момент об'єкт почне котитися, не ковзаючи, і втрачаючи швидкість з набагато повільнішою швидкістю.

    Походження умови (\ ref {eq:9.34}) досить просте. Ви можете уявити об'єкт, який котиться, не ковзаючи, як «вимірюючи поверхню», коли він котиться (або навпаки, поверхня, що вимірює окружність об'єкта, коли його різні точки притискаються до нього послідовно). Отже, після того як вона завершила оборот (\(2\pi\)радіани), вона повинна була буквально «покрити» відстань на поверхні рівне\(2\pi R\), тобто просунулося на відстань\(2\pi R\). Але те ж саме має бути правдою, пропорційно, для будь-якого кута повороту,\(\Delta \theta\) іншого, що\(2\pi\): оскільки довжина відповідної дуги є\(s = R|\Delta \theta|\),\(|\Delta \theta|\) при повороті над кутом центр маси об'єкта повинен просунутися на відстань\(|\Delta x_{cm}| = s = R|\Delta \theta|\). Ділення на\(\Delta t\) як\(\Delta t \rightarrow 0\) потім дає рівняння (\ ref {eq:9.34}).

    Figure9-6-1.png
    Малюнок\(\PageIndex{1}\): Зліва: ілюстрація прокатки без умови ковзання. Блакитна лінія на поверхні має таку ж довжину, як і дуга блакитного кольору, і буде відстань, пройдену диском, коли він повернувся через кут\(\theta\). Праворуч: швидкості для чотирьох точок на краю диска. Рожеві стрілки - це швидкості в центрі кадру маси. У системі відліку Землі швидкість центру маси, зеленим\(\vec v_{cm}\) кольором, повинна бути додана до кожного з них. Отриманий результат показаний синім кольором для двох з них.

    Зауважте, що, на відміну від Equation (8.4.12), яке воно дуже нагадує, Equation (\ ref {eq:9.34}) не є «векторною ідентичністю в маскуванні»: немає нічого подібного до Equation (9.3.6), яке ми могли б замінити його, щоб знаки автоматично виходили правильно. Ви повинні просто розглядати це як взаємозв'язок між величинами\(\vec v_{cm}\)\(\vec \omega \) і просто підбирати знаки відповідним чином для кожної обставини, виходячи з вашої конвенції щодо позитивних напрямків перекладу та обертання.

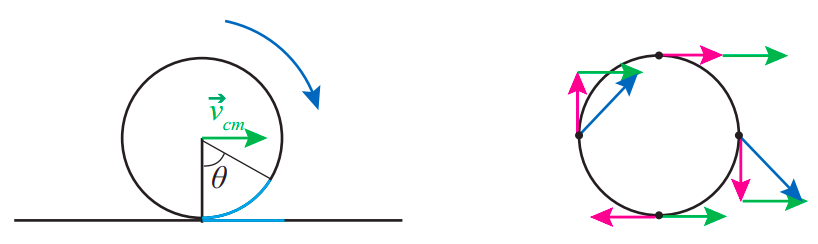
    Насправді, ми могли б використовувати Equation (9.3.6), щоб знайти швидкість будь-якої точки на колі, якщо ми перейдемо до контрольного кадру, де центр знаходиться в стані спокою, тобто центр маси (CM) опорний кадр; потім, щоб повернутися до кадру Землі, ми просто повинні додати\(\vec v_{cm}\) (як вектор) до вектора ми отримали в рамці КМ. На малюнку\(\PageIndex{1}\) показаний результат. Відзначимо, зокрема, що точка в самому низу кола має швидкість\(−R|\omega|\) у кадрі СМ, але коли ми повернемося до кадру Землі, її швидкість дорівнює\(−R|\omega| + v_{cm} = −R|\omega| + R|\omega| = 0\) (за умовою (\ ref {eq:9.34})). Таким чином, поки утримується умова прокатки без ковзання, точки (або точки) на об'єкті кочення, які на мить контактують з поверхнею, мають нульову миттєву швидкість. Це означає, що навіть якби в цій точці була сила, що діє на об'єкт (наприклад, сила статичного тертя), вона не зробила б роботи, оскільки миттєва сила\(Fv\) для прикладеної там сили завжди дорівнювала б нулю.

    Нам насправді не потрібна сила статичного тертя, щоб тримати об'єкт, що котиться по рівній поверхні (як я вже згадував вище, рух міг би в принципі йти «невимушено» назавжди), але на похилій площині все інакше. \(\PageIndex{2}\)На малюнку зображений об'єкт, що скочується вниз по похилій площині, і відповідна розширена діаграма вільного тіла.

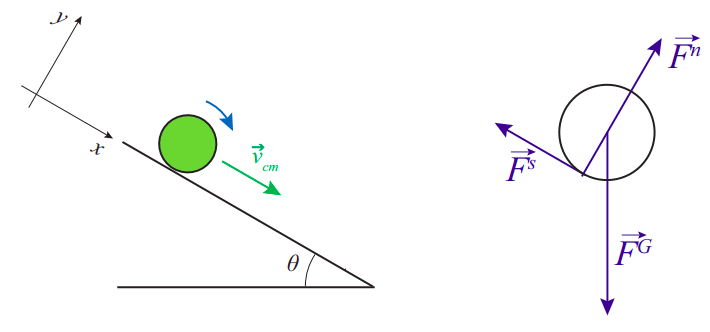
    Figure9-6-2.png
    Малюнок\(\PageIndex{2}\): Об'єкт, що скочується по похилій площині, і розширена діаграма вільного тіла. Зверніть увагу, що ні гравітація (застосована на СМ), ні нормальна сила (лінія дії якої проходить через СМ) не надають крутного моменту навколо центру маси; тільки сила статичного тертя\(\vec F^s\), робить.

    Основними рівняннями, які ми використовуємо для розв'язання руху об'єкта, є сума рівнянь сил:

    \[ \sum \vec{F}_{e x t}=M \vec{a}_{c m} \label{eq:9.35} \]

    рівняння чистого крутного моменту, з крутними моментами, прийнятими навколо центру маси 7

    \[ \sum \vec{\tau}_{e x t}=I \vec{\alpha} \label{eq:9.36} \]

    і розширення умови прокатки без ковзання, (\ ref {eq:9.34}), до прискорень:

    \[ \left|a_{c m}\right|=R|\alpha| \label{eq:9.37}.\]

    Для ситуації, показаної на малюнку\(\PageIndex{2}\), якщо ми знімемо площину як позитивний напрямок для лінійного руху, а крутні моменти за годинниковою стрілкою як негативні, ми повинні написати\(a_{cm} = −R\alpha\). У напрямку, перпендикулярному площині, ми робимо висновок з (\ ref {eq:9.35})\(F^n = Mg \cos \theta\), що рівняння нам насправді не знадобиться 8; в напрямку вздовж площини ми маємо

    \[ M a_{c m}=M g \sin \theta-F^{s} \label{eq:9.38} \]

    і рівняння крутного моменту просто дає\(−F^sR = I\alpha\), який з\(a_{cm} = −R\alpha\) стає

    \[ F^{s} R=I \frac{a_{c m}}{R} \label{eq:9.39} .\]

    Ми можемо усунути\(F^s\) між цими двома рівняннями і вирішити для\(a_{cm}\):

    \[ a_{c m}=\frac{g \sin \theta}{1+I /\left(M R^{2}\right)} \label{eq:9.40} .\]

    Тепер ви можете зрозуміти, чому раніше в семестрі ми завжди були обережні, щоб припустити, що всі об'єкти, які ми відправили вниз похилі площини, ковзали, а не котилися! Прискорення для рухомого об'єкта ніколи не дорівнює простому\(g \sin \theta\). Найпримітніше, що поправочний коефіцієнт залежить тільки від форми об'єкта, що\(MR^2\) рухається, а не від його маси або розміру, так як відношення\(I\) до не залежить від\(m\) і\(R\) для будь-якої заданої геометрії. Таким чином, наприклад, для диска, так\(I = \frac{1}{2}MR^2\)\(a_{cm} = \frac{2}{3} g \sin \theta\), тоді як для обруча\(I = MR^2\), так\(a_{cm} = \frac{1}{2} g \sin \theta\). Таким чином, будь-який диск або суцільний циліндр завжди скочується по нахилу швидше, ніж будь-який обруч або порожнистий циліндр, незалежно від маси або розміру.

    Цей досить дивовижний результат може бути краще зрозумілий з точки зору енергії. По-перше, дозвольте мені показати (результат, який дещо прострочений), що для жорсткого об'єкта, який обертається навколо осі, що проходить через його центр маси з кутовою швидкістю,\(\omega\) ми можемо записати загальну кінетичну енергію як

    \[ K=K_{c m}+K_{r o t}=\frac{1}{2} M v_{c m}^{2}+\frac{1}{2} I \omega^{2} \label{eq:9.41} .\]

    Це пояснюється тим, що для кожної частинки швидкість може бути записана як\(\vec{v}=\vec{v}_{c m}+\vec{v}^{\prime}\), де\(\vec{v}^{\prime}\) швидкість відносно центру маси (тобто в кадрі СМ). Оскільки в цьому кадрі рух є простим обертанням\( \left|v^{\prime}\right|=\omega r \), ми маємо, де\(r\) відстань частинки до осі. Отже, кінетична енергія цієї частинки буде

    \ почати {вирівняти}
    \ розрив {1} {2} м v^ {2} =\ розрив {1} {2}\ vec {v}\ cdot\ vec {v} &=\ розрив {1} {2} м\ ліворуч (\ vec {v} _ {c m} +\ vec {v} ^ {\ прайм}\ праворуч)\ cdot\ ліворуч (\ vec {v} {c m} +\ vec {v} ^ {\ правий}\ правий)\ номер\\
    &=\ розрив {1} {2} м v_ {c м} ^ {2} +\ frac {1} {2} м v^ {\ прайм 2} +м\ vec {v} _ {c м}\ cdot\ vec {v} ^ {\ простий}\ номер\\
    &=\ розриву {1} {2} м v_ {c м} ^ {2} +\ розрив {1} {2} м r^ {2}\ омега^ {2} +\ vec {v} _ {c m}\ cdot\ vec {p} ^ {\ прайм}\ мітка {еква:9.42}
    \ кінець {вирівнювання}

    (Зверніть увагу, як я використав крапковий добуток для обчислення величини в квадраті вектора.) На останньому рядку величина\(\vec{p}^{\prime}\) - це імпульс цієї частинки в кадрі СМ. Додавання цих моментів для всіх частинок повинно дати нуль, оскільки, як ми бачили в попередньому розділі, центр кадру маси є нульовим імпульсом кадру. Потім додавання внесків усіх частинок до першого та другого членів у\ ref {eq:9.42} дає рівняння (\ ref {eq:9.41}).

    Повертаючись до нашого тіла кочення, використовуючи Equation (\ ref {eq:9.41}) і умова прокатки без ковзання (\ ref {eq:9.34}), ми бачимо, що відношення поступальної до обертальної кінетичної енергії дорівнює

    \[ \frac{K_{c m}}{K_{r o t}}=\frac{m v_{c m}^{2}}{I \omega^{2}}=\frac{m R^{2}}{I} \label{eq:9.43} .\]

    Кількість енергії, доступної для прискорення об'єкта спочатку є лише гравітаційною потенційною енергією системи об'єкт-земля, яка повинна бути розділена між поступальною та обертальною у пропорції (\ ref {eq:9.43}). Об'єкт з пропорційно більшим\(I\) - це той, який для заданої кутової швидкості потребує більшої кінетичної енергії обертання, оскільки більша частина його маси знаходиться далеко від осі обертання. Це залишає менше енергії доступною для його поступального руху.

    Ресурси

    На жаль, у нас насправді не буде достатньо часу в цьому семестрі, щоб вивчити далі багато цікавих ефектів, які випливають з векторної природи Equation (9.4.2), але ви принаймні підсвідомо знайомі з деякими з них, якщо ви коли-небудь навчилися їздити на велосипеді! Кілька цікавих інтернет-посилань (деякі з яких, можливо, можуть надихнути хороший проект Honors!) є наступні:

    6 Існує простий аргумент, заснований на теорії відносності Ейнштейна, який показує, що нескінченно жорсткий об'єкт не може існувати: якби це сталося, ви могли б миттєво відправити сигнал з одного його кінця на інший, просто натиснувши або потягнувши за свій кінець. На практиці такий рух не може досягти іншого кінця швидше, ніж швидкість звукової хвилі (тобто хвилі стиснення) в матеріалі. Ми будемо вивчати такі хвилі (які мають на увазі, що середовище не є нескінченно жорстким) в Главі 12.

    7 Ви можете відчувати себе трохи неспокійно з приводу того, що CM кадр тепер є прискореним, а отже, і неінерційним, кадром. Як ми знаємо, що рівняння (\ ref {eq:9.36}) навіть застосовується там? Це, дійсно, нетривіальний момент. Однак, як ми побачимо в наступному розділі, перебування в рівномірно-прискореному опорному кадрі еквівалентно знаходженню в рівномірному гравітаційному полі, і ми щойно показали, що для всіх цілей, пов'язаних з крутним моментом, можна розглядати таке поле як єдину силу, прикладену до центру маси об'єкта. Така сила (або «псевдосила» в даному випадку) явно не сприяє крутному моменту навколо центру мас, і тому Equation (\ ref {eq:9.36}) застосовується в кадрі СМ.

    8 Якщо ми не намагалися відповісти на таке питання, як «наскільки крутим повинен бути літак, щоб кочення без ковзання стало неможливим?»