9.5: Статика
- Page ID
- 74576
Статика - це галузь механіки, що стосується сил і напружень 5, необхідних для підтримки системи в стані спокою, в стабільному рівновазі - так що вона не буде рухатися, згинатися або руйнуватися. Це, очевидно, надзвичайно важливо в машинобудуванні (особливо в машинобудуванні). У вступному курсі фізики ми можемо займатися нею лише на дуже елементарному рівні, ігноруючи взагалі деформацію протяжних об'єктів, таких як дошки та балки (і пов'язані з ними напруги), і просто накладаючи дві прості умови статичної рівноваги: по-перше, сітчаста (зовнішня) сила на системі повинен бути нуль, щоб переконатися, що її центр маси залишається в стані спокою; а по-друге, чистий (зовнішній) крутний момент на системі також повинен бути нульовим, щоб вона не оберталася. Ці умови можуть бути символічно виражені як
\ begin {вирівнювання}
\ сума\ vec {F} _ {e x t} =0\ nonumber\
\ sum\ vec {\ tau} _ {е х т} =0\ мітка {еква:9.27}
\ кінець {вирівнювання}
Ви можете запитати про те, в якій точці слід розрахувати крутний момент. Відповідь полягає в тому, що поки виконується перша умова (сума сил дорівнює нулю), це не має значення! Доказ простий, але ви можете пропустити його, якщо вам це не цікаво.
Припустимо, у вас є дві точки, A і B, навколо яких слід обчислити крутний момент. Нехай\(\vec r_{A1}\),\(\vec r_{A2}\),... бути векторами положення точок прикладання сил\(\vec F_{1}\),\(\vec F_{2}\)..., щодо точки А, і\(\vec r_{B1}\),..., те ж саме, але щодо точки Б. Якщо ви повернетеся до малюнка 1.3.1 (в главі 1), ви можете побачити, що\(\vec r_{B2}\) ці вектори відрізняються від першого набору єдиним постійним вектором\(\vec r_{AB}\), який дає положення точки B відносно точки A: і\(\vec{r}_{A 1}=\vec{r}_{A B}+\vec{r}_{B 1}\) т.д. тоді для суми крутних моментів навколо А ми маємо
\ почати {вирівняти}
\ vec {r} _ {A 1}\ раз\ vec {F} _ {1} +\ vec {r} _ {A 2}\ times\ vec {F} _ {2} +\ ldots &=\ вліво (\ vec {r} _ {A B} _ {R} _ {B 1}\ праворуч)\ times\ vec {F} _ {1} + ліворуч (\ vec {r} _ {A B} +\ vec {r} _ {A 2}\ праворуч)\ раз\ vec {F} _ {2} +\ ldots\ nonumber\\
&=\ vec {r} _ {A B}\ раз\ вліво (\ vec {F} _ {1} +\ vec {F} _ {2}\ ldots\ праворуч) +\ vec {r} _ {B 1}\ раз\ vec {F} _ {1} +\ vec {r} _ {B 2}\ times\ vec {F} _ {2} +\ ldots\ мітка {еква:9.28}
\ кінець {вирівнювання}
Перший член на останньому рядку дорівнює нулю, якщо сума всіх сил дорівнює нулю, а те, що залишилося - це сума всіх крутних моментів навколо Б. Це, дійсно, для статики про 1 blems, поки ми виконуємо, не має значення про те\(\sum \vec{F}_{e x t}=0\), яку точку ми виберемо для обчислення крутного моменту. Природним вибором є центр маси системи, оскільки це, як правило, точка високої симетрії, але ми також можемо вибрати точку, де є багато прикладених сил, і тому швидко позбутися від них (оскільки їх крутний момент навколо цієї точки буде нульовим).
Те, як все це працює, мабуть, найкраще проілюстровано прикладом. \(\PageIndex{1}\)На малюнку зображена класична, сходи, що спираються на стіну. Ескіз зліва показує задіяні кути і розміри, тоді як правильна розширена діаграма вільного тіла, що показує всі сили та їх точки застосування, знаходиться праворуч.
Мінімальна кількість сил, необхідних для балансування системи, становить чотири: вага сходів (що діє в центрі мас), нормальна сила від землі, інша нормальна сила від стіни, і сила статичного тертя від землі, що перешкоджає ковзанню сходів. У реальному житті також повинна бути сила статичного тертя від стіни, спрямована вгору (також для запобігання ковзання); і, звичайно, якщо на сходах є людина, вона буде надавати на неї додаткову силу вниз (рівну її вазі), прикладене в якій би точці вона не стояла. Я не збираюся розглядати жодне з цих ускладнень, просто щоб зробити приклад простим, але з ними можна було б впоратися точно так само.
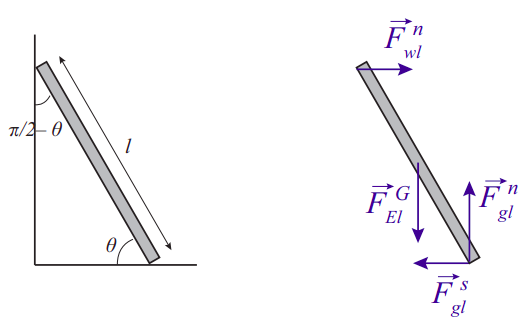
З умовністю про те, що векторна величина без стрілки зверху представляє величину цього вектора, рівняння балансу вертикальних сил читає
\[ F_{g l}^{N}-m g=0 \label{eq:9.29} .\]
Для горизонтальних сил ми маємо
\[ F_{w l}^{N}-F_{g l}^{s}=0 \label{eq:9.30} .\]
Потім, приймаючи крутний момент навколо точки, де сходи контактує з землею, жодна з двох сил, застосованих у цій точці, не сприятиме, і умова, що сума крутних моментів дорівнює нулю, стає
\[ F_{w l}^{N} l \sin \theta-m g \frac{l}{2} \cos \theta=0 \label{eq:9.31} .\]
Це пояснюється тим, що кут, зроблений силою тяжіння з вектором положення його точки застосування\(\frac{\pi}{2}-\theta\), є, і\(\sin \left(\frac{\pi}{2}-\theta\right)=\cos \theta\). З першого рівняння ми отримуємо це\(F_{g l}^{N}=m g\); з другого ми отримуємо, що інша нормальна сила,\(F_{w l}^{N}=F_{g l}^{s}\). Якщо підставити це в (\ ref {eq:9.31}), і скасуємо\(l\), довжина сходів, отримаємо умову
\[ F_{g l}^{s}=\frac{1}{2} m g \cot \theta \label{eq:9.32} .\]
Але сила статичного тертя не може перевищувати\(\mu_{s} F_{g l}^{N}=\mu_{s} m g\), тому, встановивши праву частину (\ ref {eq:9.32}) нижче або дорівнює\(\mu_s mg\), і скасувавши загальний коефіцієнт mg, отримаємо умову
\[ \cot \theta \leq 2 \mu_{s}, \quad \text { or } \quad \tan \theta \geq \frac{1}{2 \mu_{s}} \label{eq:9.33} \]
за мінімальний кут,\(\theta\) під яким ми можемо нахилити сходи до того, як вона прослизне і впаде.
5 «Стрес» - це «розподілена» сила в витягнутому об'єкті, безперервно змінюється від однієї точки до іншої.
