9.4: Крутний момент

Ми, нарешті, в змозі відповісти на питання, коли зберігається кутовий імпульс? Для цього ми просто візьмемо похідну по відношенню до часу, і скористаємося законами Ньютона, щоб з'ясувати, за яких обставин вона дорівнює нулю.\(\vec L\)

Почнемо з частинки і розрахуємо

\[ \frac{d \vec{L}}{d t}=\frac{d}{d t}(m \vec{r} \times \vec{v})=m \frac{d \vec{r}}{d t} \times \vec{v}+m \vec{r} \times \frac{d \vec{v}}{d t} \label{eq:9.19} .\]

Перший член з правого боку йде як\(\vec v \times \vec v\), який дорівнює нулю. Другий термін можна переписати як\(m \vec{r} \times \vec{a}\). Але, згідно з другим законом Ньютона,\(m \vec a = \vec F_{net}\). Отже, робимо висновок, що

\[ \frac{d \vec{L}}{d t}=\vec{r} \times \vec{F}_{n e t} \label{eq:9.20} .\]

Таким чином, кутовий імпульс, як і звичайний імпульс, буде збережений, якщо чиста сила на частинці дорівнює нулю, але також, і це важлива різниця, коли чиста сила паралельна (або антипаралельна) вектору положення. Для руху по колу з постійною швидкістю саме так і відбувається: сила, що діє на частинку, - це доцентрова сила, яку можна записати як\(\vec F_c = m \vec{a}_c = −m\omega^2 \vec r\) (використовуючи Equation (9.3.10))\(\vec{r} \times \vec{F}_{c}=0\), так і кутовий момент постійний.

Величина\(\vec{r} \times \vec{F}\) називається крутним моментом сили навколо точки (початок, з якого\(\vec r\) розраховується, як правило, точка повороту або центр обертання). Позначається вона грецькою літерою\(\tau\), «тау»:

\[ \vec{\tau}=\vec{r} \times \vec{F} \label{eq:9.21} .\]

Для розширеного об'єкта або системи швидкість зміни вектора кутового моменту задавалася б сумою крутних моментів всіх сил, що діють на всі частинки. Для кожного крутного моменту потрібно використовувати вектор положення частинки, на яку діє сила. Як і було при розрахунку швидкості зміни звичайного імпульсу розширеної системи (розділ 6.1), третій закон Ньютона при невеликому додатковому припущенні призводить до скасування крутних моментів за рахунок внутрішніх сил ³, і тому нам залишається тільки

\[ \vec{\tau}_{e x t, a l l}=\frac{d \vec{L}_{s y s}}{d t} \label{eq:9.22} .\]

Само собою зрозуміло, що всі крутні моменти і кутові моментипотрібно розраховувати щодо однієї і тієї ж точки.

Крутний момент сили навколо точки в основному є мірою того, наскільки ефективною буде сила, що викликає обертання навколо цієї точки. Так як\(|\vec{r} \times \vec{F}|=r F \sin \theta\), можна помітити, що це залежить від трьох речей: величини сили, відстані від центру обертання до точки, куди прикладається сила, і кут, під яким прикладається сила. Все це можна зрозуміти досить добре з малюнка\(\PageIndex{1}\) нижче, особливо якщо вам коли-небудь доводилося використовувати гайковий ключ для затягування або ослаблення болта:

Малюнок\(\PageIndex{1}\): Крутний момент навколо точки O кожної з показаних сил є мірою того, наскільки він ефективний у змушенні стрижня обертатися навколо цієї точки.

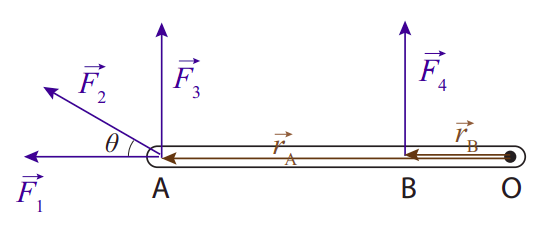
Ясно, що сила взагалі не\(\vec F_1\) викличе обертання, і відповідно його крутний момент дорівнює нулю (так як паралельно\(\vec r_A\)). З іншого боку, з усіх показаних сил найефективнішою є\(\vec F_3\): вона застосовується найдалі від O, для найбільшого важеля (знову ж таки, подумайте про свій досвід з гайковими ключами). Він також перпендикулярний стрижню, для максимального ефекту (\(\sin \theta\)= 1). Сила\(\vec F_2\), навпаки, хоча і застосовується в точці А, знаходиться в невигідному становищі через відносно невеликий кут, з яким вона робить\(\vec r_A\). Якщо ви уявляєте, розбиваючи його на компоненти, паралельні та перпендикулярні стрижню, лише перпендикулярний компонент (чия величина\(F_2 \sin \theta\)) буде ефективним у спричиненні обертання; інший компонент, той, що паралельний стрижню, буде витрачено даремно, як\(\vec F_1\).

Для того, щоб обчислити крутний момент, ми в основному повинні знайти, для кожної сили, компонент, який перпендикулярний вектору положення його точки застосування. Зрозуміло, що для цього ми більше не можемо представляти розширене тіло як просту крапку, як ми це робили для діаграм вільного тіла в главі 6. Що нам потрібно, так це більш ретельний ескіз об'єкта, просто досить деталізований, щоб ми могли сказати, як далеко від центру повороту і під яким кутом прикладається кожна сила. Така діаграма називається розширеною діаграмою вільного тіла.

Малюнок\(\PageIndex{1}\) може бути прикладом розширеної діаграми вільного тіла, для об'єкта, на який діють чотири сили. Зазвичай, однак, замість того, щоб малювати вектори,\(\vec r_A\) і\(\vec r_B\) ми просто вказуємо їх довжини на схемі (а може бути, навіть залишити їх взагалі, якщо ми не хочемо перевантажувати діаграму деталями). Я покажу кілька прикладів розширених діаграм вільного тіла в наступних кількох розділах.

Як зазначено вище, для обчислення крутного моменту кожної сили, що діє на витягнутий об'єкт, слід використовувати вектор\(\vec r\) положення точки, куди прикладається сила. Це, як правило, однозначно для контактних сил ⁴, але як щодо сили тяжіння? В принципі, сила тяжіння діяла б на всі частинки, що складають тіло, і нам доведеться скласти всі відповідні моменти:

\[ \vec{\tau}^{G}=\vec{r}_{1} \times \vec{F}_{E, 1}^{G}+\vec{r}_{2} \times \vec{F}_{E, 2}^{G}+\ldots \label{eq:9.23} .\]

Однак ми можемо значно спростити це, зазначивши, що (біля поверхні Землі, у будь-якому випадку) всі сили\(F_{E, 1}^{G}\),\(F_{E, 2}^{G}\)... вказують в одному напрямку (тобто вниз), і всі вони пропорційні масі кожної частинки. Якщо я дозволю загальній масі об'єкта бути\(M\), а загальна сила, обумовлена гравітацією на об'єкт\(\vec{F}_{E, o b j}^{G}\), то я маю,,...\(\vec{F}_{E, 1}^{G}=m_{1} \vec{F}_{E, o b j}^{G} / M\)\(\vec{F}_{E, 2}^{G}=m_{2} \vec{F}_{E, o b j}^{G} / M\), і я можу переписати рівняння (\ ref {eq:9.23}) як

\[ \vec{\tau}^{G}=\frac{m_{1} \vec{r}_{1}+m_{2} \vec{r}_{2}+\ldots}{M} \times \vec{F}_{E, o b j}^{G}=\vec{r}_{c m} \times \vec{F}_{E, o b j}^{G} \label{eq:9.24} \]

\(\vec r_{cm}\)де - вектор положення центру мас об'єкта. Отже, щоб знайти крутний момент через тяжіння на витягнутому об'єкті, просто візьміть загальну силу тяжіння на об'єкт (тобто вагу об'єкта), яку слід застосувати в його центрі маси. (Очевидно, що тоді крутний момент ваги навколо самого центру маси буде нульовим, але в деяких важливих випадках об'єкт може обертатися в точці, відмінній від його центру маси.)

Повертаючись до Equation (\ ref {eq:9.22}), основний посил цього розділу (іншого, звичайно, крім самого визначення крутного моменту) полягає в тому, що швидкість зміни кутового моменту об'єкта або системи дорівнює чистому крутному моменту за рахунок зовнішніх сил. З цього випливають два особливих результату. По-перше, якщо чистий зовнішній крутний момент дорівнює нулю, кутовий імпульс буде збережений, як це було, зокрема, для зіткнення, проілюстрованого раніше, на малюнку 9.2.3, між частинкою і стрижнем, що обертається на одному кінці. Єдиною зовнішньою силою в цьому випадку була сила, що чиниться на стрижень, в точці повороту, самим стрижнем, але крутний момент цієї сили навколо цієї точки, очевидно, дорівнює нулю, оскільки\(\vec r = 0\), тому наше припущення, що загальний кутовий імпульс навколо цієї точки був збережений, було законним.

По-друге, якщо\(\vec L = I\vec \omega\) тримає, а момент інерції\(I\) не змінюється з часом, ми можемо переписати рівняння (\ ref {eq:9.22}) як

\[ \vec{\tau}_{\text {ext}, a l l}=I \vec{\alpha} \label{eq:9.25} \]

який в основному обертальний еквівалент Ньютона, другий закон,\(\vec F = m\vec a\). Ми будемо широко використовувати це в решті частини цієї глави.

Нарешті, зауважте, що ситуації, коли момент інерції системи\(I\), зміни з часом відносно легко організувати для будь-якої деформованої системи. Особливо цікавий випадок, коли зовнішній крутний момент дорівнює нулю, тому\(L\) постійний, і зміна,\(I\) отже, призводить до зміни\(\omega = L/I\): так, наприклад, фігуристка може змусити себе обертатися швидше, наблизивши руки до осі обертання (зменшуючи її \(I\)), і, навпаки, уповільнити її обертання, витягнувши руки. Це можна зробити навіть за відсутності точки контакту з землею: наприклад, дайвери з високим бортом також обертаються таким чином, коли вони згортають своє тіло в кульку. Зверніть увагу, що протягом усього занурення кутовий момент дайвера навколо свого центру мас постійний, оскільки єдина сила, що діє на нього (гравітація, нехтуючи опором повітря) має нульовий крутний момент близько цієї точки.

У всіх щойно згаданих випадках кутовий момент постійний, але змінюється кінетична енергія обертання. Це пов'язано з роботою, яку виконують внутрішні сили (тіла ковзанника або дайвера), перетворюючи деяку внутрішню енергію (наприклад, еластичну м'язову енергію) в обертальну кінетичну енергію, або навпаки. Зручний вираз для обертальної кінетичної енергії системи при\(\vec L = I\vec \omega\) утриманні

\[ K_{r o t}=\frac{1}{2} I \omega^{2}=\frac{L^{2}}{I} \label{eq:9.26} \]

який явно показує, як\(K\) зміниться, якщо\(I\) змінився і\(L\) залишався постійним.

---

³ Додаткове припущення полягає в тому, що сила між будь-якими двома частинками лежить уздовж лінії, що з'єднує дві частинки (що означає, що вона паралельна або антипаралельна вектору\(\vec{r}_{1}-\vec{r}_{2}\)). У такому випадку,\(\vec{r}_{1} \times \vec{F}_{12}+\vec{r}_{2} \times \vec{F}_{21}=\left(\vec{r}_{1}-\vec{r}_{2}\right) \times \vec{F}_{12}=0\). Більшість сил в природі задовольняють цій умові.

⁴ Насправді сили тертя та нормальні сили можуть бути «розподілені» по всій поверхні, але, якщо об'єкт має достатню симетрію, зазвичай нормально змусити їх «діяти» в середній точці цієї поверхні. Це можна довести за лініями виведення для гравітації, що слідує.