8.7: Розширені теми

Приклад\(\PageIndex{1}\): Staying on track

(Цей приклад вивчає ситуацію, яку ви могли б легко налаштувати експериментально вдома (ви можете використовувати цілу сферу замість напівсфери!) , хоча, щоб отримати цифри, щоб працювати, вам дійсно потрібно переконатися, що тертя між поверхнею і обраним вами об'єктом дійсно незначне. По суті, той самий математичний підхід може бути використаний для вивчення проблеми лижника, що переїжджає магнат, або автомобіль втрачає контакт з дорогою, якщо він їде занадто швидко через пагорб.)

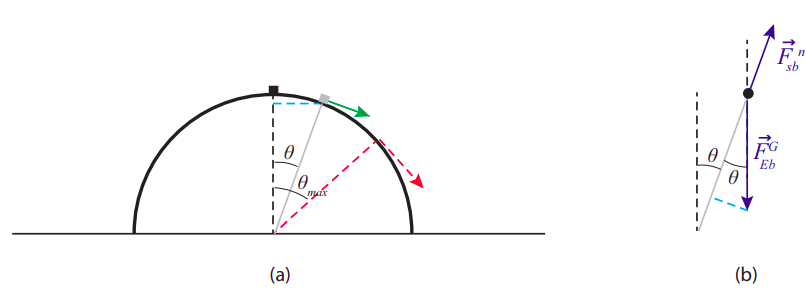
Невеликий об'єкт розміщується у верхній частині гладкого (без тертя) купола у формі напівсфери радіуса\(R\), і дається невеликий поштовх, тому він починає ковзати вниз по куполу, спочатку рухаючись дуже повільно\(\left(v_{i} \simeq 0\right)\), але набираючи швидкість, як він йде, поки в якийсь момент він не злетить з поверхні.

1. У той момент, коли об'єкт втрачає контакт з поверхнею, який кут робить вектор його положення (з початком у центрі сфери) з вертикаллю?
2. Як далеко від сфери приземляється об'єкт?

Малюнок\(\PageIndex{1}\): Об'єкт (малий блок), що ковзає по напівсферичному куполу. На малюнку (а) показано кут,\(\theta_{max}\) під яким об'єкт відлітає (червона пунктирна лінія), і менший загальний кут\(\theta\). На кресленні (б) показана діаграма вільного тіла, відповідна куту\(\theta\).

Рішення

(а) Як ми бачили в розділі 8.4, для того, щоб об'єкт рухався по дузі кола, потрібна\(mv^2/r\) доцентрова сила величини. Поки наш об'єкт контактує з поверхнею, сили, що діють на нього, є нормальною силою (яка вказує вздовж радіального напрямку, тому вона вносить негативний внесок у відцентрову силу) та гравітація, яка має складову\(mg \cos \theta\) вздовж радіуса, до центру кола (Див. Рис.\(\PageIndex{1}\) (b) пунктирну світло-блакитну лінію). Отже, рівняння доцентрової сили читає

\[ \frac{m v^{2}}{R}=m g \cos \theta-F^{n} \label{eq:8.46} .\]

Наступне, що нам потрібно зробити, це знайти значення швидкості v для заданого кута\(\theta\). Якщо розглядати об'єкт як частинку, то його єдиною енергією є кінетична енергія, і\(\Delta K = W_{net}\) (Рівняння (7.2.8)), де\(W_{net}\) проводиться робота над частинкою чистою силою, що діє на неї. Нормальна сила завжди перпендикулярна зміщенню, тому вона не працює, тоді як гравітація завжди вертикальна і працює\(W_{grav} = −mg\Delta y\) (приймаючи вгору як позитивну,\(\Delta y\) так і негативну). Насправді з малюнка\(\PageIndex{1}\) (а) (слідувати пунктирною синьою лінією) видно\(\theta\), що для заданого кута висота предмета над землею дорівнює\(R \cos \theta\), тому вертикальне зміщення від його початкового положення дорівнює

\[ \Delta y=-(R-R \cos \theta) \label{eq:8.47} \]

Отже, ми маємо, для зміни кінетичної енергії,

\[ \frac{1}{2} m v^{2}-\frac{1}{2} m v_{i}^{2}=m g R-m g R \cos \theta \label{eq:8.48} .\]

Припустимо, як нам сказано в тексті задачі, що ми отримуємо\(v_{i} \simeq 0\)\(v^2 \simeq 2gR − 2gR \cos \theta \), і використовуючи це в Equation (\ ref {eq:8.46})

\[ 2 m g-2 m g \cos \theta=m g \cos \theta-F^{n} \label{eq:8.49} \]

або\(F^n = 3mg \cos \theta −2mg\). Це показує, що\(F^n\) починається (коли\(\theta\) = 0), маючи своє звичайне значення\(mg\), а потім він стає поступово меншим, коли об'єкт ковзає вниз. Точка, де об'єкт втрачає контакт з поверхнею, коли\(F^n\) = 0, і це відбувається для

\[ 3 \cos \theta_{max} = 2 \label{eq:8.50} \]

або\(\theta_{\max }=\cos ^{-1}(2 / 3)=48.2^{\circ} \).

Нагадуючи\(\Delta y = −(R − R \cos \theta)\), що, ми бачимо, що коли\( \cos \theta\) = 2/3, об'єкт впав на відстань\(R\) /3; ставимо інакше, його висота над землею в момент відльоту становить 2\(R\) /3, або 2/3 від початкової висоти.

(б) Це просто проблема снаряда зараз. Нам залишається лише знайти значення початкових умов (\(x_i\),\(y_i\),\(v_{x,i}\) і\(v_{y,i}\)) і підставити в рівняння (8.2.2). Оглянувши фігуру, можна помітити, що, в той момент, коли об'єкт злітає,

\ begin {вирівнювання}
&x_ {i} =R\ sin\ theta_ {\ max} =0,745 R\ nonumber\\
&y_ {i} =R\ cos\ theta_ {\ max} =0,667 R\ мітка {e:8.51}.
\ end {вирівняти}

Крім того, ми виявили вище\(v^{2} \simeq 2 g R-2 g R \cos \theta\), що, і коли\(\theta = \theta_{max}\) це дає\(v^2 = 0.667gR\), або\(v=0.816 \sqrt{g R} \). Кут проекції в даному випадку дорівнює\(−\theta_{max}\); тобто початкова швидкість снаряда (пунктирна червона стрілка на рис.\(\PageIndex{1}\) (а)) знаходиться під кутом 48,2\(^{\circ}\) нижче позитивної\(x\) осі, тому маємо:

\ почати {вирівняти}
&v_ {x, i} =v_ {i}\ cos\ theta_ {\ max} =0.544\ sqrt {г R}\ номер\\
&v_ {y, i} =-v_ {i}\ sin\ theta_ {\ max} =-0.609\ sqrt {г R}\ мітка {еква:8.52}
\ кінець {вирівнювання}

Тепер ми просто використовуємо ці результати в Eqs. (8.2.2). Зокрема, ми хочемо знати, скільки часу потрібно, щоб об'єкт досяг землі, тому ми використовуємо останнє рівняння (8.2.2) з\(y\) = 0 і вирішуємо для\(t\):

\[ 0=y_{i}+v_{y, i} t-\frac{1}{2} g t^{2} \label{eq:8.53} \]

Результат є\(t=0.697 \sqrt{R / g}\). (Вам не потрібно носити «\(g\)» на всьому протязі; було б нормально замінити 9.8 м/с ² для нього. Я щойно зберігав його в символічній формі до цих пір, щоб дати зрозуміти, що величини, які ми отримуємо, матимуть правильні одиниці.) Підставивши це в рівняння для\(x\), отримаємо

\[ x=x_{i}+v_{x, i} t=0.745 R+0.544 \sqrt{g R} \times 0.697 \sqrt{R / g}=1.125 R \label{eq:8.54} \]

(Зверніть увагу, як\(g\) скасовується, щоб ми отримали такий же результат на будь-якій планеті!) Оскільки сфера має радіус\(R\), об'єкт падає на деяку відстань\(0.125R\) від сфери.

Приклад\(\PageIndex{2}\): Going around a banked curve

Інженери проїжджої частини часто фіксують криву, особливо якщо це дуже щільний поворот, тому автомобілям не доведеться покладатися на тертя поодинці, щоб забезпечити необхідну доцентрову силу. На малюнку зображений автомобіль, що йде навколо такої кривої, яку ми можемо змоделювати як дугу окружності радіуса\(r\). З точки зору\(r\), кут банку\(\theta\), і коефіцієнт статичного тертя, знайти максимальну безпечну швидкість навколо кривої.

Малюнок\(\PageIndex{2}\): Автомобіль, що рухається навколо кривої кривої (ескіз та діаграма вільного кузова). Центр кола - справа.

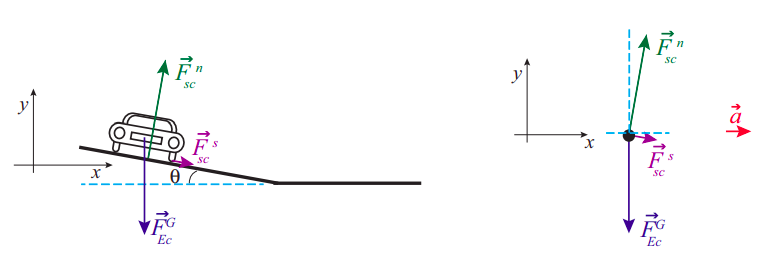
На малюнку показаний відповідний вибір осей для даної задачі. Критерій - знову ж таки, вибрати осі так, щоб одна з них збігалася з напрямком прискорення. При цьому прискорення все доцентрове, тобто спрямоване, горизонтально, до центру кола, по якому їде автомобіль.

Може здатися дивним бачити силу статичного тертя, спрямовану вниз по схилу, але нагадайте, що для автомобіля, що повертає на рівну поверхню, вона була б спрямована всередину (до центру кола), так що це природне продовження цього. Загалом, завжди потрібно намагатися уявити, в який бік ковзає об'єкт, якщо тертя зникне зовсім:\(\vec F^s\) повинен вказувати в протилежному напрямку. Таким чином, для автомобіля, що рухається з розумною швидкістю, напрямок, в якому він буде ковзати вгору по схилу, і це означає, що\(\vec F^s\) повинен вказувати вниз по схилу. Але, для автомобіля, який просто сидить нерухомо на нахиленій дорозі,\(\vec F^s\) повинен вказувати вгору, і ми побачимо через мить, що в цілому існує мінімальна швидкість, необхідна для того, щоб сила статичного тертя вказувала в обраному нами напрямку.

Крім цього, головна відмінність корпусу з плоскою поверхнею полягає в тому, що тепер нормальна сила має складову уздовж напрямку прискорення, тому вона допомагає тримати автомобіль рухатися по колу. З іншого боку, зауважте, що тепер ми втрачаємо (для доцентрових цілей) трохи сили тертя, оскільки вона спрямована трохи вниз. Це, однак, з лишком компенсується тим, що нормальна сила зараз більше, ніж це було б для рівної поверхні, так як машина зараз, так би мовити, дещо «в'їжджає» в дорогу.

Пунктирні сині лінії на діаграмі вільного тіла призначені для позначення того, що кут\(\theta\) банку також є кутом між нормальною силою і позитивною\(y\) віссю, а також кут, який\(\vec F^s\) робить нижче позитивної\(x\) осі. Звідси випливає, що складовими цих двох сил по зображених осях є:

\ begin {вирівнювання}
&F_ {x} ^ {n} =F^ {n}\ sin\ тета\ nonumber\\
&F_ {y} ^ {n} =F^ {n}\ cos\ тета\ мітка {еква:8.55}
\ кінець {вирівнювання}

і

\ begin {вирівнювання}
&F_ {x} ^ {s} =F^ {s}\ cos\ тета\ nonumber\\
&F_ {y} ^ {n} =-F^ {s}\ sin\ тета\ мітка {еква:8.56}
\ кінець {вирівнювання}

Рівняння вертикальної сили тоді:

\[ 0=m a_{y}=F_{y}^{n}+F_{y}^{s}-F^{G}=F^{n} \cos \theta-F^{s} \sin \theta-m g \label{eq:8.57} .\]

Це показує, що\(F^n = (mg + F^s \sin \theta)/ \cos \theta \) дійсно більше, ніж просто\(mg\) для цієї проблеми, і повинен збільшуватися в міру\(\theta\) збільшення кута (оскільки\(\cos \theta\) зменшується зі збільшенням\(\theta\)). Горизонтальне рівняння таке:

\[ m a_{x}=F_{x}^{n}+F_{x}^{s}=F^{n} \sin \theta+F^{s} \cos \theta=\frac{m v^{2}}{r} \label{eq:8.58} \]

де я вже підставив значення доцентрового прискорення для\(a_x\). Рівняння (\ ref {eq:8.57}) і (\ ref {eq:8.58}) утворюють систему, яку потрібно розв'язати для двох невідомих\(F^n\) і\(F^s\). В результаті виходить:

\ begin {вирівнювання}
&F ^ {n} =м г\ cos\ theta+\ frac {м v^ {2}} {r}\ sin\ тета\ nonumber\\
&F^ {s} =-м g\ sin\ theta+\ frac {m v^ {2}} {r}\ cos\ тета\ мітка {еква:8.59}.
\ end {вирівняти}

Зверніть увагу, що друге рівняння\(F^s\) стало б від'ємним, якщо\( v^{2}<g r \tan \theta \). Це означає, що нижче цієї швидкості сила статичного тертя повинна фактично вказувати вгору по схилу, як обговорювалося вище. Ми можемо назвати саме цю швидкість, для якої\(F^s\) стає нульовою,\(v_{no \: friction}\):

\[ v_{\text {no friction }}=\sqrt{g r \tan \theta} \label{eq:8.60} .\]

Це означає, що можна розташувати банківський кут так, щоб автомобіль, що рухається з певною швидкістю, не довелося б взагалі покладатися на тертя, щоб зробити криву: нормальна сила була б в самий раз, щоб забезпечити необхідне доцентрове прискорення. Автомобіль, що рухається з такою швидкістю, не відчував би ні потягнутий вниз, ні штовхнув вгору по схилу. Однак автомобіль, що йде швидше, ніж це, як правило, «злітає», і статична сила тертя буде потрібно, щоб витягнути його і тримати на кривій, тоді як автомобіль, що рухається повільніше, як правило, ковзає вниз і повинен бути підштовхнутий вгору силою тертя. Тертя, таким чином, забезпечує діапазон безпечних швидкостей для їзди в цьому випадку, так само, як це було в корпусі з плоскою поверхнею.

Ми можемо обчислити максимальну безпечну швидкість, як ми робили раніше, нагадуючи, що ми повинні мати завжди\(F^{s} \leq \mu_{s} F^{n}\). Заміна Eqs. (\ ref {eq:8.59}) в цьому виразі, і вирішуючи for\(v\), отримаємо умову

\[ v_{\max }=\sqrt{g r} \sqrt{\frac{\mu_{s}+\tan \theta}{1-\mu_{s} \tan \theta}} \label{eq:8.61} .\]

Це відтворює наш результат (8.4.5) для\(\theta\) = 0 (рівнинна дорога), як слід.

Щоб поставити в це деякі цифри, припустимо, що крива має радіус 20 м, а коефіцієнт статичного тертя між шинами і дорогою дорівнює\(\mu_s\) = 0,7. Потім за рівну поверхню отримуємо\(v_{max}\) = 11,7 м/с, або близько 26 миль/год, тоді як для берегового кута\(\theta\) = 10\(^{\circ}\) (кут, обраний для малюнка вище) отримуємо\(v_{max}\) = 14 м/с, або близько 31 миль/год.

Рівняння (\ ref {eq:8.61}) фактично вказує на те, що максимальна швидкість «стане нескінченною» для кінцевого кута банку, а саме\(1 − \mu_s \tan \theta = 0\), якщо, або\(\tan \theta = 1/ \mu_s\) (якщо\(\mu_s\) = 0,7, це відповідає\(\theta\) = 55\(^{\circ}\)). Це математично правильно, але, звичайно, ми не можемо сприймати це буквально: це припускає, що немає меж тому, наскільки велика нормальна сила може надати проїжджа частина, не зазнаючи шкоди, а також яка\(F^s\) може стати довільно великою, поки вона залишається нижче прив'язаного\(F^{s} \leq \mu_{s} F^{n} \). Жодне з цих припущень не буде триматися в реальному житті на дуже великих швидкостях. Також кут\(\theta=\tan ^{-1}\left(1 / \mu_{s}\right) \) занадто крутий: нагадаємо, що згідно з рівнянням (8.3.11) сила тертя зможе утримувати об'єкт (спочатку в спокої) від ковзання вниз по схилу якщо\(\tan \theta \leq \mu_{s}\), що для\(\mu_s\) = 0,7 означає\(\theta \leq 35^{\circ}\). Отже, з кутом банку 55\(^{\circ}\) ви могли б їхати на кривій, за умови, що ви йдете досить швидко, але ви не могли припаркуватися на ньому - автомобіль буде ковзати вниз! Підсумок, використовуйте Equation (\ ref {eq:8.61}) лише для помірних значень\(\theta\)... і не перевищуйте,\(\theta=\tan ^{-1} \mu_{s}\) якщо ви хочете, щоб автомобіль міг повільно їздити по кривій, не ковзаючи вниз у кювет.

Приклад\(\PageIndex{3}\): Rotating frames of reference- centrifugal force and coriolis force

Уявіть, що ви перебуваєте всередині обертається циліндричної радіусної кімнати\(R\). На підлозі знаходиться металева шайба, відстань\(r\) від осі обертання, утримувана на місці за допомогою електромагніту. У якийсь час ви вимикаєте електромагніт і шайба вільно ковзає без тертя. Знайдіть, де шайба б'є об стіну, і покажіть, що, якщо вона була не надто далеко від стіни для початку, здається, що вона рухалася прямо до стіни, як тільки її звільнили.

Рішення

Картинка виглядає так, як показано нижче, до спостерігача в інерційній рамці, дивиться вниз. Шайба починається в точці А, з миттєвою швидкістю,\(\omega r\) спрямованою прямо вліво в момент її звільнення, тому вона просто рухається прямо (в інерційній рамці), поки не вдариться про стіну в точці Б. З показаного трикутника блакитного кольору ми бачимо, що він проходить відстань\(\sqrt{R^{2}-r^{2}}\), яка займає на час

\[ \Delta t=\frac{\sqrt{R^{2}-r^{2}}}{\omega r} \label{eq:8.62} .\]

В цей час приміщення обертається проти годинникової стрілки на кут\(\Delta \theta_{room} = \omega \Delta t\):

\[ \Delta \theta_{\text {room}}=\frac{\sqrt{R^{2}-r^{2}}}{r} \label{eq:8.63} .\]

Малюнок\(\PageIndex{3}\): Рух шайби (блакитний) та стіни (пурпурний), як видно інерційним спостерігачем.

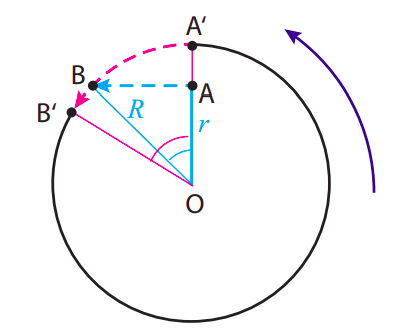
Це кут, показаний пурпуровим кольором на малюнку. В результаті такого обертання точка А,\(^{\prime}\) яка спочатку знаходилася на стіні прямо поперек від шайби, перемістилася (слідуючи пунктирною лінією пурпурного кольору) в позицію B\(^{\prime}\), тому спостерігачеві в обертовій кімнаті, дивлячись на речі з точки О, з'являється шайба головою до стіни і дрейфує трохи праворуч при цьому.

Блакитний кут на малюнку, який ми могли б назвати\(\Delta \theta_{part}\), має дотичну рівну\(\sqrt{R^{2}-r^{2}} / r\), тому ми маємо

\[ \Delta \theta_{\text {room}}=\tan \left(\Delta \theta_{\text {part}}\right) \label{eq:8.64} .\]

Це говорить нам, що два кути будуть досить близькими, якщо вони досить малі, що відбувається, якщо шайба починається досить близько до стіни в першу чергу. На малюнку для наочності показаний випадок\(r = 0.7R\), коли, який дає\(\Delta \theta_{room}\) = 1,02 рад, а\(\Delta \theta_{part} = \tan^{−1}(1.02)\) = 0,8 рад. Бо\(r = 0.9R\), з іншого боку, можна знайти\(\Delta \theta_{room}\) = 0,48 рад, а\(\Delta \theta_{part} = \tan^{−1}\) (0,48) = 0,45 рад.

З точки зору псевдосил (сил, які фізично не існують, але можуть бути введені для математичного опису руху об'єктів в неінерційних системах відліку), неінерційний спостерігач сказав би, що шайба прямує до стіни через відцентрової сили (тобто сили вказуючи подалі від центру обертання), і при цьому він дрейфує вправо через так званої сили Коріоліса.