25.4: Приклад використання векторів у фізиці

У цьому розділі наведено короткий огляд деяких застосувань векторів у фізиці.

Кінематика та векторні рівняння

Кінематика - опис положення і руху об'єкта (глави 3 і 4). Закони фізики - це принципи, які в кінцевому підсумку дозволяють визначити, як змінюється положення об'єкта з часом. Наприклад, Закони Ньютона - це математичні рамки, які вводять поняття сили і маси для того, щоб змоделювати і визначити, як об'єкт буде рухатися через простір.

Ми часто використовуємо вектор позиції\(\vec r(t)\), щоб описати положення об'єкта як функцію часу. Оскільки об'єкт може рухатися, вектор положення є функцією часу. Вектор положення - це спеціальний вектор в тому сенсі, що його слід вважати закріпленим у просторі; вектор положення об'єкта вказує від початку системи координат до місця розташування об'єкта.

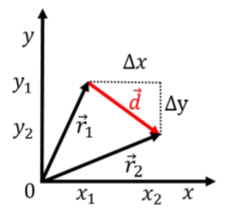
Три компоненти вектора положення в декартових координатах, є\(x\),\(y\), і\(z\) координати об'єкта:\[\begin{aligned} \vec r(t) = \begin{pmatrix} x(t) \\ y(t) \\ z(t) \\ \end{pmatrix}\end{aligned}\] де три координати об'єкта є функціями часу, якщо об'єкт може рухатися. Припустимо, що об'єкт спочатку знаходився\(\vec r_1=(x_1, y_1, z_1)\) в положенні в якийсь час\(t=t_1\), і що пізніше, в той час\(t=t_2\), об'єкт знаходився в якості другої позиції,\(\vec r_2=(x_1, y_1, z_1)\). Ми можемо визначити вектор зміщення\(\vec d\), як вектор з позиції\(\vec r_1\) в положення\(\vec r_2\):\[\begin{aligned} \vec d = \vec r_2 - \vec r_1 =\begin{pmatrix} x_2-x_1 \\ y_2-y_1 \\ z_2-z_1 \\ \end{pmatrix} = \begin{pmatrix} \Delta x \\ \Delta y \\ \Delta z \\ \end{pmatrix}\end{aligned}\] Вектор зміщення такий, що можна додати вектор\(\vec d\) до вектора\(\vec r_1\) описати нове положення об'єкта в часі\(t_2\):\[\begin{aligned} \vec d &= \vec r_2 - \vec r_1\\ \therefore \vec r_2 &= \vec r_1 + \vec d\end{aligned}\] Компоненти вектора зміщення,,\(\Delta x\)\(\Delta y\), і\(\Delta z\) відповідають переміщенням (пройденої відстані) уздовж\(x\), \(y\), І\(z\) осі відповідно. Це проілюстровано для двовимірного випадку на малюнку A1.4.1.

Малюнок A1.4.1: Ілюстрація вектора зміщення\(\vec d = \vec r_{2} − \vec r_{1}\), для об'єкта, який був розташований у положенні\(\vec r_{1}\) в той час\(t_{1}\) і в положенні\(\vec r_{2}\) в часі\(t_{2}\).

Вектор швидкості об'єкта, визначається як вектор переміщення\(\vec v=(v_x, v_y, v_z)\), розділений на кількість часу (скаляр)\(\vec d\), що минув\(\Delta t=t_2-t_1\), в той час як об'єкт переміщений відповідним зміщенням:\[\begin{aligned} \vec v = \frac{\vec d}{\Delta t}=\begin{pmatrix} \frac{\Delta x}{\Delta t} \\ \frac{\Delta y}{\Delta t} \\ \frac{\Delta z}{\Delta t} \\ \end{pmatrix}\end{aligned}\] Ми використовували властивість, що ділить a вектор за скаляром (\(\Delta t\)) визначається як поділ кожної складової на скаляр. Якщо ми випишемо компоненти вектора швидкості явно, ми маємо:\[\begin{aligned} \begin{pmatrix} v_x \\ v_y \\ v_z \\ \end{pmatrix} = \begin{pmatrix} \frac{\Delta x}{\Delta t} \\ \frac{\Delta y}{\Delta t} \\ \frac{\Delta z}{\Delta t} \end{pmatrix}\end{aligned}\] Тобто ми можемо розглядати кожен рядок у цьому «векторному рівнянні» як незалежне рівняння. Тобто, коли ми пишемо векторне рівняння:\[\begin{aligned} \vec v = \frac{\vec d}{\Delta t}\end{aligned}\] ми насправді просто використовуємо скорочені позначення для написання трьох незалежних рівнянь, які є істинними для кожного окремого компонента векторів:\[\begin{aligned} v_x &= \frac{\Delta x}{\Delta t} \\ v_y &= \frac{\Delta y}{\Delta t} \\ v_z &= \frac{\Delta z}{\Delta t} \\\end{aligned}\] Всякий раз, коли ми пишемо рівняння за допомогою векторів, ми дійсно виписуємо декілька рівняння все відразу, по одному для кожного компонента. Другий закон Ньютона:\[\begin{aligned} \vec F = m \vec a\end{aligned}\] таким чином відповідає трьом (скалярним) рівнянням:\[\begin{aligned} F_x &= ma_x\\ F_y &= ma_y\\ F_z &= ma_z\\\end{aligned}\]

Робота і скалярні добутки

Як ми побачимо, «робота» - це скалярна величина, яка дозволяє нам визначити зміну швидкості (у квадраті) об'єкта, що виникає внаслідок сили, що чиниться над певним зміщенням (Глава 7). І сила, і зміщення є векторними величинами (сила має величину і чиниться в певному напрямку). Робота\(W\), виконана силою над зміщеннями\(\vec F\)\(\vec d\), визначається як:\[\begin{aligned} W = \vec F \cdot \vec d\end{aligned}\] Теорема робочої енергії говорить нам, що ця робота пов'язана зі зміною швидкості в квадраті об'єкта, коли він рухається вздовж вектора переміщення \(d\). Якщо робота дорівнює нулю, об'єкт має однакову швидкість на початку і в кінці зміщення. Якщо робота позитивна, об'єкт рухається швидше в кінці зміщення (і повільніше, якщо робота негативна). Одновимірний приклад показаний на малюнку А1.4.2, який показує силу,\(\vec F\) прикладену до блоку, коли він ковзає вздовж землі на відстань\(d\) (представлена вектором зміщення\(\vec d\)).

Малюнок А1.4.2: Приклад сили,\(\vec F\) що прикладається до об'єкта під час його переміщення вздовж вектора зміщення\(\vec d\).

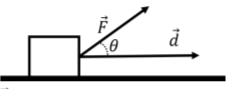
Інтуїтивно має сенс, що тільки горизонтальна складова сили сприяла б зміні швидкості об'єкта в міру його руху по горизонтальній траєкторії, визначеної вектором\(\vec d\). Вертикальна складова сили не сприяє зміні швидкості об'єкта. Таким чином, робота (зміна швидкості), повинна залежати тільки від складової сили, яка паралельна вектору зміщення. Скалярний добуток дозволяє формалізувати це в рівнянні. Скалярний добуток задається:\[\begin{aligned} \vec F \cdot \vec d = Fd\cos\theta = F_{\parallel}d\end{aligned}\] де ми ввели\(F_{\parallel} = F\cos\theta\) як компонент\(\vec F\), що паралельно\(\vec d\) (див. Рис. Таким чином, скалярний продукт «вибирає» компонент,\(\vec F\) що паралельно\(\vec d\), що саме те, що нам потрібно для того, щоб робота мала сенс.

Використання векторів для опису обертального руху

Часто нам потрібно описати обертальний рух у фізиці. Якщо об'єкт обертається, потрібно вказати:

1. Вісь, навколо якої обертається об'єкт
2. Напрямок навколо цієї осі, в якому об'єкт обертається (наприклад, за годинниковою стрілкою або проти годинникової стрілки)
3. Як швидко обертається об'єкт

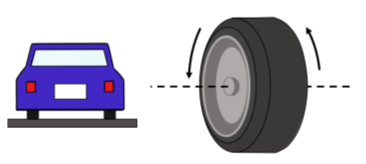
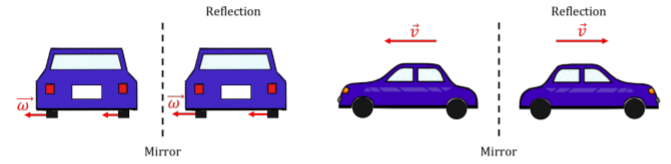
Введено новий тип вектора, «осьовий вектор», для опису такого роду обертального руху. Ми вибираємо напрямок вектора, яке буде співлінійним з віссю обертання і величиною вектора, щоб представляти швидкість, з якою обертається об'єкт. Таким чином, нам залишається два варіанти для напрямку вектора. Для прикладу розглянемо колеса на автомобілі, який віддаляється від вас (рис. А1.4.3, автомобіль рухається на сторінку). Вісь обертання - це вісь колеса, тому ми знаємо, що вектор, що описує обертання колеса (вектор кутової швидкості), повинен вказувати або вліво, або вправо.

Малюнок А1.4.3: Колеса на автомобілі, який від'їжджає від вас.

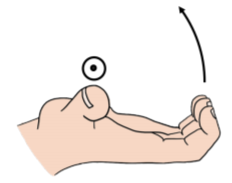
Напрямок вектора вибираємо за допомогою іншого правила правої руки. Ми будемо називати це «правилом правої руки для осьових векторів», щоб відрізнити його від правила правої руки для перехресного добутку. При використанні правила правої руки для осьових векторів вектор вказує в напрямку великого пальця при скручуванні пальців у напрямку обертання, як на малюнку А1.4.4. Для автомобіля, що віддаляється від вас, колеса будуть обертатися таким чином, що найближча до вас точка рухається вгору, а найдальша точка рухається вниз. Використовуючи правило правої руки, знаходимо, що вектор обертання вказує вліво.

Малюнок A1.4.4: Використання правила правої руки для осьових величин. При цьому напрямок обертання - проти годинникової стрілки при погляді на сторінку (напрямок, в якому скручуються пальці), тому вектор обертання вказує за межі сторінки (напрямок великого пальця).

Ми повинні відрізняти осьові вектори від «істинних» векторів, оскільки вони не поводяться як істинні вектори у всіх випадках. Наприклад, уявіть, що є гігантське дзеркало, яке проходить паралельно дорозі (рис. А1.4.5). Коли автомобіль відбивається в дзеркалі, відбитий автомобіль також буде віддалятися від вас. Це означає, що колеса будуть повертатися в тому ж напрямку, що і раніше, тому вектор обертання все одно вказує вліво. Тепер розглянемо справжній вектор, подібний вектору швидкості. Якщо вектор швидкості спочатку вказував вліво (тобто якщо автомобіль рухався вліво), відбитий автомобіль буде рухатися вправо. Отже, ми очікуємо, що справжній вектор змінить напрямки, коли це буде відображено таким чином. Оскільки вектор обертання не завжди поводиться як справжній вектор, ми називаємо його осьовим вектором або «псевдовектором».

Малюнок А1.4.5: Зліва: Вектор кутової швидкості обертання коліс\(\vec ω\), який вказує вліво, також вказує зліва в відображенні. Праворуч: Вектор швидкості, що вказує вліво, вказує вправо у відображенні автомобіля. Вектор кутової швидкості називається «осьовим» або «псевдо» вектором, оскільки він не змінює напрямок під відображенням.

Крутний момент і векторні продукти

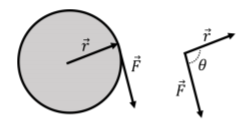
Ми введемо поняття крутного моменту, щоб описати, як сила може змусити об'єкт обертатися. Розглянемо диск, проілюстрований на малюнку A1.4.6, який вільно обертається навколо осі, яка проходить через її центр і яка перпендикулярна площині сторінки. На краю диска\(\vec F\) прикладається сила (уявіть, що тягне за струну, прикріплену до краю диска), в положенні, зміщеному від осі обертання вектором\(\vec r\). \(\vec \tau\)Крутний момент сили навколо центру диска визначається як:\[\begin{aligned} \vec\tau=\vec r\times \vec F\end{aligned}\] і представляє, наскільки сила\(\vec F\) сприятиме тому, щоб диск обертався навколо своєї осі. Якби вектор сили був паралельний вектору\(\vec r\), диск не обертався б; якщо ви витягнете диск назовні, він не буде обертатися навколо свого центру. Однак якщо сила буде перпендикулярна вектору\(\vec r\) (тобто дотичній до окружності диска), то воно максимально змусить диск обертатися. Величина крутного моменту (перехресного добутку)\(\theta\) задається:\[\begin{aligned} \tau =rF\sin\theta=F_{\perp}r=Fr_\perp\end{aligned}\] де кут між векторами при розміщенні хвоста до хвоста, як в правій частині малюнка А1.4.6. В останніх двох рівнях ми визначили\(F_\perp=F\sin\theta\) або\(r_\perp=r\sin\theta\) посилаємося на частину вектора,\(\vec F\) яка перпендикулярна вектору,\(\vec r\) або частини вектора\(\vec r\), яка перпендикулярна вектору \(\vec F\). Тобто векторний добуток «відбирає» ту частину вектора, яка перпендикулярна іншому, що є саме тією властивістю, яка нам потрібна для фізичної величини крутного моменту.

Малюнок А1.4.6: Сила\(\vec F\), чиниться в площині диска в положенні, заданому вектором\(\vec r\) щодо центру диска.

Вправа\(\PageIndex{1}\)

Посилаючись на малюнок А1.4.6, в який бік вказує вектор крутного моменту?

1. праворуч
2. ліворуч
3. поза сторінкою
4. на сторінку

Відповідь