25.3: Векторна алгебра

У цьому розділі ми опишемо різні алгебраїчні операції, які можуть бути виконані за допомогою векторів.

Множення/ділення вектора на скаляр

Можна помножити (або розділити) вектор на скаляр (число). Припустимо, що нам дано вектор\(\vec v=(v_x, v_y, v_z)\) і скаляр\(a\). Множення\(a\vec v\) визначається як новий вектор, скажімо\(\vec w\), складовими якого є складові\(\vec v\) множення на\(a\):\[\begin{aligned} \vec w = a\vec v = (av_x, a v_y, av_z)\end{aligned}\] Аналогічно, поділ вектора на скаляр визначається аналогічно діленням кожного Декартова складова за скаляром:\[\begin{aligned} \vec w = \frac{\vec v}{a} = \left(\frac{v_x}{a}, \frac{v_y}{a}, \frac{v_z}{a}\right)\end{aligned}\]

Вправа\(\PageIndex{1}\)

Що відбувається з довжиною вектора, якщо вектор помножити на\(2\) (a scalar)?

1. Довжина подвоюється
2. Довжина зменшується вдвічі
3. Довжина в чотири рази
4. Це залежить від напрямку вектора

Відповідь

Зокрема, це дозволяє легко визначити одиничний вектор\(\hat v\), який вказує в тому ж напрямку, що і\(\vec v\):\[\begin{aligned} \hat v = \frac{\vec v}{v}\end{aligned}\] де\(v\) знаходиться (скалярна) величина\(\vec v\).

Додавання/віднімання двох векторів

Сума двох векторів,\(\vec a\) і\(\vec b\), знаходить шляхом додавання компонентів двох векторів. Аналогічно різниця між двома векторами знаходить шляхом віднімання компонентів. Наприклад, якщо\(\vec c=\vec a+\vec b\), компоненти\(\vec c\) задаються за допомогою:\[\begin{aligned} \vec c &= \vec a + \vec b = \begin{pmatrix} a_x \\ a_y \\ \end{pmatrix} + \begin{pmatrix} b_x \\ b_y \\ \end{pmatrix}\\ \therefore \begin{pmatrix} c_x \\ c_y \\ \end{pmatrix} &=\begin{pmatrix} a_x+b_x \\ a_y+b_y \\ \end{pmatrix}\end{aligned}\] де ми вирішили використовувати позначення «вектор стовпця». Векторне позначення стовпців підкреслює той факт, що алгебра (додавання, віднімання) виконується самостійно на\(y\) компонентах\(x\) і. Таким чином, ми можемо використати цю суму еквівалентно як два скалярні рівняння, по одному для кожної координати: Таким чином,\[\begin{aligned} c_x &= a_x+b_x\\ c_y &= a_y+b_y\end{aligned}\] вектори можуть бути використані як короткі позначення для представлення декількох рівнянь (одне рівняння на компонент). Коли ми використовуємо вектори для написання рівняння, такого як:\[\begin{aligned} \vec F = m\vec a\end{aligned}\] ми дійсно маємо на увазі, що існує одне скалярне рівняння на компонент векторів:\[\begin{aligned} F_x &= ma_x\\ F_y &= ma_y\\ F_z &= ma_z\end{aligned}\]

Приклад\(\PageIndex{1}\)

З огляду на два вектори,\(\vec a=2\hat x+3\hat y\), and \(\vec b=5\hat x-2\hat y\), calculate the vector \(\vec c= 2\vec a- 3\vec b\).

Рішення:

Це можна легко вирішити алгебраїчно шляхом збору термінів для кожного компонента,\(\hat x\) і\(\hat y\):\[\begin{aligned} \vec c &= 2\vec a- 3\vec b\\ &=2 (2\hat x+3\hat y) - 3 (5\hat x-2\hat y) \\ &=(4\hat x+6\hat y)-(15\hat x-6\hat y) \\ &=(4-15)\hat x + (6+6) \hat y\\ &= -11 \hat x + 12 \hat y\end{aligned}\] Ми можемо вважати ці операції виконуваними незалежно від компонентів:\[\begin{aligned} c_x&=2a_x-3b_x=-11\\ c_y&=2a_y-3b_y=12\end{aligned}\]

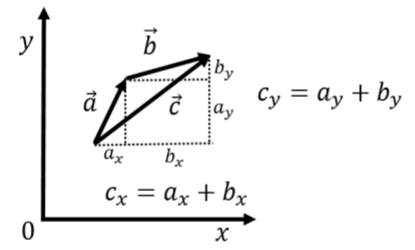
Геометрично можна легко візуалізувати додавання і віднімання векторів. Це проілюстровано на малюнку A1.3.1 для випадку додавання векторів\(\vec a\) та\(\vec b\) отримання вектора\(\vec c\). Геометрично суму векторів\(\vec a\) і\(\vec b\) (іноді ще називають «результуючими») можна знайти за допомогою:

1. Розміщення «хвоста» вектора\(\vec b\) на «голові»\(\vec a\) (подумайте про стрілку, загострена частина - це голова, а пір'яста частина - хвіст)
2. Малювання вектора, що йде від хвоста вектора\(\vec a\) до голови вектора\(\vec b\).

Малюнок А1.3.1: Геометричне складання векторів\(\vec a\) і\(\vec b\) шляхом їх розміщення «голова до хвоста».

Віднімання двох векторів геометрично проводиться так само, як додавання. Наприклад, вектор\(\vec c\), заданий також\(\vec c=\vec a -\vec b\) може бути виражений як\(\vec c = \vec a + (-1) \vec b\). Тобто спочатку помножте вектор\(\vec b\) на мінус 1 (який просто змінює свій напрямок), потім додайте цей вектор, «голова до хвоста», до вектора\(\vec a\).

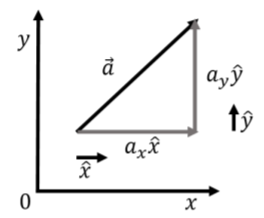
Тепер, коли ми знаємо, як додавати вектори, ми можемо краще зрозуміти позначення\(\vec a = a_x \hat x+ a_y\hat y\). Це не просто позначення, але насправді є алгебраїчно правильним. Це означає: «помножте вектор\(\hat x\) на\(a_x\) (тим самим надаючи йому довжину\(a_x\)), а потім додайте\(a_y\) раз вектор\(\hat y\)». Це проілюстровано на малюнку А1.3.2, на якому показані одиничні вектори\(\hat y\),\(\hat x\) причому, які потім множаться на\(a_x\) і\(a_y\), відповідно, а потім складаються разом «голова до хвоста».

Малюнок А1.3.2: Ілюстрація того, що позначення насправді\(\vec a = a_{x}\hat x + a_{y}\hat y\) є векторним доповненням\(a_{x}\hat x\) і\(a_{y}\hat y\).

скалярний добуток

Існує два способи «множення» векторів: «скалярний добуток» і «векторний добуток». Скалярний добуток (або «точковий добуток») приймає два вектори і призводить до скалярного (числа). Векторний добуток (або «перехресний добуток») приймає два вектори і призводить до третього вектора.

Скалярний\(\vec a \cdot \vec b\) добуток двох векторів\(\vec a\) і\(\vec b\) визначається наступним чином:\[\begin{aligned} \vec a \cdot \vec b=a_xb_x +a_yb_y\end{aligned}\] Тобто один множить окремі компоненти двох векторів, а потім додає ці добутки для кожного компонента. Це легко поширюється на тривимірний випадок, додаючи\(a_zb_z\) до суми термін. Скалярний добуток також пов'язаний з кутом між двома векторами при розміщенні векторів «хвіст до хвоста», як на малюнку A1.3.3\[\begin{aligned} \vec a \cdot \vec b= ab\cos\theta\end{aligned}\]

Малюнок A1.3.3: Ілюстрація кута між векторами\(\vec a\) і\(\vec b\) коли вони розміщені хвіст до хвоста.

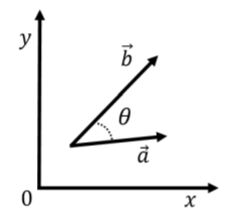
Скалярний добуток між двома векторами фіксованої довжини буде максимальним, коли два вектори паралельні (\(\cos\theta=1\)) і нуль, коли вектори перпендикулярні (\(\cos\theta =0\)). Таким чином, скалярний добуток корисний, коли ми хочемо обчислити величини, які є максимальними, коли два вектори паралельні.

Вправа\(\PageIndex{2}\)

Вектори\(\vec a\) і\(\vec b\) на трьох діаграмах нижче мають однакову величину. Замовте діаграми від тієї, яка дає найменший скалярний добуток\(\vec a\cdot \vec b\) до найбільшого скалярного добутку.

Малюнок А1.3.4: Поставте їх в порядок величини їх скалярного добутку.

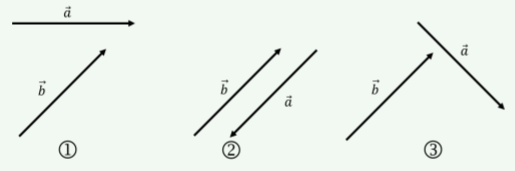
Відповідь

\(2<3<1\)

Векторний добуток

Векторний (або перехресний) добуток приймає два вектори для отримання третього вектора, який взаємно перпендикулярний обом векторам. Векторний добуток має значення лише у трьох вимірах. Два вектори, які не є співлінійними, тобто вони не можуть бути розташовані так, щоб вони лежали уздовж однієї лінії, завжди можуть бути використані для визначення площини в трьох вимірах. Перехресний добуток цих двох векторів дасть третій вектор, який перпендикулярний площині (робить його перпендикулярним обом векторам).

Алгебраїчно три складові векторного\(\vec a\times \vec b\) добутку векторів\(\vec a\) і\(\vec b\) зустрічаються наступним чином:

\[ \vec a \times \vec b =\begin{pmatrix} a_yb_z - a_z b_y\\ a_zb_x - a_x b_z\\ a_xb_y - a_y b_x\\ \end{pmatrix}\]

Однією важливою властивістю, яку слід зазначити, є те, що\(\vec a \times \vec b = -\vec b \times \vec a\); тобто перехресний продукт не є комутативним (порядок має значення). Величина вектора, отриманого перехресним добутком, задається:

\[ ||\vec a \times \vec b ||=ab\sin\theta\]

де\(\theta\) - кут між векторами\(\vec a\) і\(\vec b\) коли вони розміщуються хвіст до хвоста (рис. А1.3.3). Вектор, отриманий з перехресного добутку, буде нульовим (мають нульову довжину), якщо вектори\(\vec a\) і\(\vec b\) паралельні, і матиме максимальну довжину, коли вони перпендикулярні. Перехресний добуток корисний для визначення величин, які є максимальними, коли два вектори перпендикулярні.

Геометрично можна визначити напрямок перехресного добутку двох векторів за допомогою «правила правої руки». Щоб відрізнити його від іншого правила правої руки (див. Розділ А1.4), ми будемо називати його «правилом правої руки для перехресного виробу»). Це робиться за допомогою правої руки, вирівнявши великий палець з першим вектором, а вказівний - з другим вектором. Хрестове виріб буде вказувати в напрямку вашого середнього пальця (коли ви тримаєте середній палець перпендикулярно іншим двома пальцями). Це проілюстровано на малюнку А1.3.5. Таким чином, ви часто можете уникнути використання Equation A1.3.1 і замість цього використовувати правило правої руки для визначення напрямку перехресного добутку і Рівняння A1.3.2, щоб знайти його величину.

Малюнок А1.3.5: За допомогою правила правої руки для перехресних добутків знайти напрямок перехресного добутку векторів\(\vec a\)\(\vec b\) (вгору) і (на сторінку).

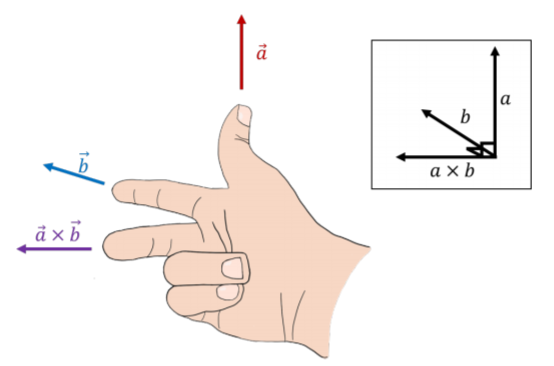
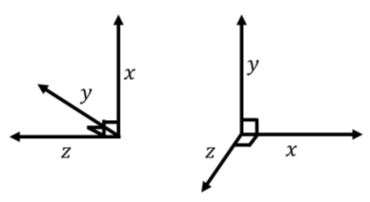
Одиничні вектори, що визначають систему координат, мають такі властивості щодо перехресного добутку:\[\begin{aligned} \vec x \times \vec y &= \vec z\\ \vec y \times \vec z &= \vec x\\ \vec z \times \vec x &= \vec y\\\end{aligned}\] Щоб ці властивості були правильними, слід зазначити, що напрямок\(z\) осі в трьох вимірах задається вибором\(x\) і \(y\)сокири. Тобто можна вільно вибирати напрямок\(y\) осей\(x\) і, які потім визначають площину, до якої\(z\) вісь буде перпендикулярна. Напрямок\(z\) осі потрібно вибирати так, щоб\(\vec x \times \vec y = \vec z\) (це гарантує, що система координат «правша»), як на малюнку А1.3.6.

Малюнок A1.3.6: Дві можливі орієнтації для тривимірної системи координат. Ви можете підтвердити за допомогою правила правої руки, що\(z\) вісь є поперечним твором\(\vec x × \vec y\).