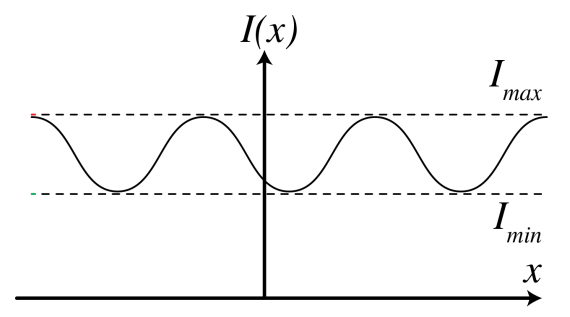
5.10: Видимість бахроми

Last updated
Save as PDF

Page ID: 78807

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Ми бачили, що коли інтерференційний термін\(\operatorname{Re}\left\langle U_{1}^{*} U_{2}\right\rangle\) зникає, не утворюються бахроми, тоді як коли цей термін ненульовий, є бахроми. Видимість бахроми виражається безпосередньо в вимірних кількостях (тобто в інтенсивності замість полів). Враховуючи деяку схему інтенсивності перешкод\(\PageIndex{1}\),\(I(x)\) як на малюнку, видимість визначається як\[\mathcal{V}=\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }} . \quad \text { fringe visibility. } \nonumber \]

Наприклад, якщо у нас є два ідеально когерентних, монохроматичних точкових джерела, що випромінюють поля\(U_{1}, U_{2}\) з інтенсивностями\(I_{1}=\left|U_{1}\right|^{2}, I_{2}=\left|U_{2}\right|^{2}\), то інтерференційна картина - з (5.6.13):\[I(\tau)=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos (\omega \tau+\varphi) . \nonumber \]

Ми тоді отримуємо\[I_{\max }=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}}, \quad I_{\min }=I_{1}+I_{2}-2 \sqrt{I_{1} I_{2}}, \nonumber \]\(\mathrm{SO}\)\[\mathcal{V}=\frac{2 \sqrt{I_{1} I_{2}}}{I_{1}+I_{2}} \nonumber \]

У разі\(I_{1}=I_{2}\), якщо знаходимо\(\mathcal{V}=1\). У зворотному випадку, де\(U_{1}\) і абсолютно\(U_{2}\) незв'язні, ми знаходимо,\[I(\tau)=I_{1}+I_{2}, \nonumber \] з чого випливає,\[I_{\max }=I_{\min }=I_{1}+I_{2}, \nonumber \] що дає\(\mathcal{V}=0\).

5.9.1.jpg — Рисунок\(\PageIndex{1}\): Ілюстрація\(I_{\max }\) та\(I_{\min }\) інтерференційної картини\(I(x)\), яка визначає видимість\(\mathcal{V}\).