3.9: Телескоп

Last updated
Save as PDF

Page ID: 78800

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Телескоп збільшує зображення сітківки віддаленого об'єкта. Як і складний мікроскоп, він також складається з об'єктиву та окуляра, як показано на малюнку\(\PageIndex{1}\). Об'єкт на цьому малюнку знаходиться на великій, але кінцевій відстані; отже, зображення формується об'єктивом відразу після його другої фокусної точки. Окуляр робить віртуальне збільшене зображення, яке потрібно розглядати розслабленим оком. Тому посередницький образ об'єктиву повинен знаходитися в межах фокусної відстані\(f_{i}^{e}\) від окуляра. Кінцеве зображення перевернуто.

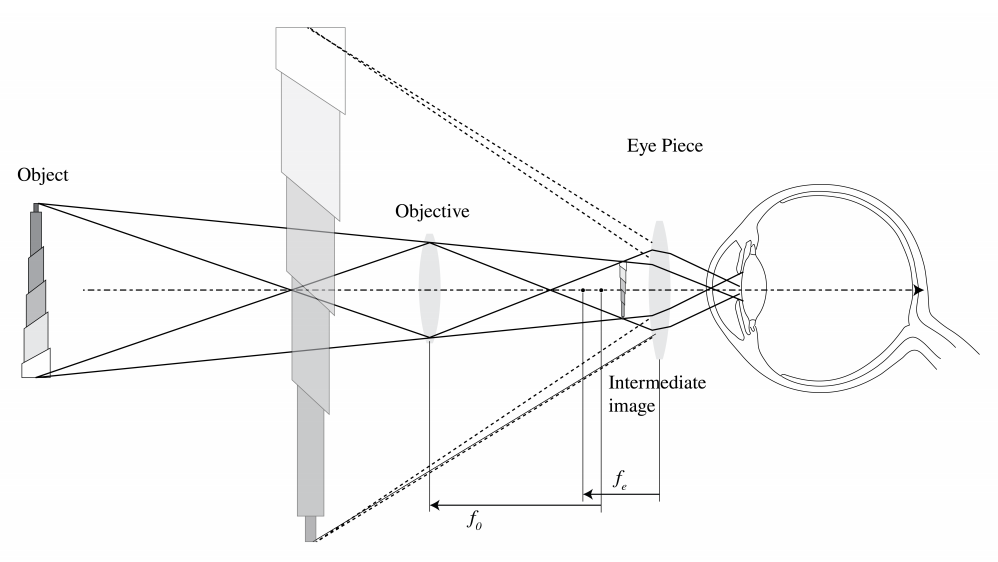
3.8.1.jpg — Малюнок\(\PageIndex{1}\): Кеплерівський астрономічний телескоп.

Як було видно раніше, кутове збільшення таке:\(\mathrm{MP}=\alpha_{a} / \alpha_{u}\) де\(\alpha_{u}\) половина кута конуса світла, який був би зібраний без телескопа і\(\alpha_{a}\) є половиною кута видимого конуса променів, що надходять від віртуального зображення шматочка ока. З трикутників\(F_{o}^{o b j} B C\) і\(F_{i}^{e} D E\) на малюнку\(\PageIndex{1}\) ми бачимо, що\[\mathrm{MP}=-\frac{f_{i}^{o b j} \mid}{f_{i}^{e}} \nonumber \]

3.8.2.jpg — Малюнок\(\PageIndex{2}\): Кути променя для телескопа