2.11: Товсті лінзи

На малюнку II.16 показана товста лінза індексу\(n_2\), об'єкт O та зображення I. Для хорошої міри я\(n_1\) поставив середовище індексу ліворуч від лінзи та середовище\(n_3\) індексу праворуч від лінзи.

Якщо вам дано положення О, чи можете ви обчислити положення зображення?

Ну а легко обчислити сходження,\(C_1\) коли світло надходить на першу поверхню. Тоді ми можемо легко обчислити конвергенцію,\(C_2\) просто додаючи потужність першого інтерфейсу. І, якщо ми знаємо\(C_3\) (Так, є руб) ми можемо легко обчислити\(C_4\). Ми бачимо, що ключ до вирішення проблем з товстими лінзами полягає в тому, щоб знати, як конвергенція змінюється з відстанню, тому ми зробимо це нашою наступною метою.

На малюнку II.17 показаний промінь світла\(n_2\), в середовищі індексу, що сходиться до точки Р, яка знаходиться на відстані\(x\) від площини А\(C_2 = n_2/x\). Коли він прибуває на площину B, яка знаходиться на відстані D від площини А, його збіжність є\( C_3 =n_2/(x-D)\). Коли ми усуваємо\(x\), отримуємо

\[ C_3 = \frac{n_2C_2}{n_2 - DC_2} \label{eq:2.11.1} \]

для формули, яка говорить нам, як конвергенція змінюється з відстанню.

Повернемося тепер до проблеми малюнка II.16.

Приклад\(\PageIndex{1}\)

Припустимо, радіуси кривизни першої і другої граней складають 15 і 25 см відповідно, а відстань між гранями - 50 см. Показник заломлення скла\(n_2\) = 1,60. Припустимо, що зліва від лінзи є вода (\(n_1\)= 1,33), а праворуч від лінзи є якась рідина з показником заломлення 1,42. Об'єкт знаходиться на 30 см зліва від першої грані. Де зображення?

Рішення

Розрахунок відбувається наступним чином (Рівняння\ ref {eq:2.11.1}):

\[ \begin{align*} C_1 &= -\dfrac{1.33}{30} = -0.044333 \, \text{cm}^{-1} \\[4pt] C_2 &= C_1 + \dfrac{1.60-1.33}{+15} = -0.026333 \, \text{cm}^{-1} \\[4pt] C_3 &= \dfrac{1.60\times C_2}{1.60 - 50 \times C_2} = -0.014446 \, \text{cm}^{-1} .\end{align*}\]

Зверніть увагу, що світло розходиться на той час, коли він досягає другої грані.

\[ C_4 = C_3 + \dfrac{1.42-1.60}{-25} = -0.007246 \, \text{cm}^{-1}. \nonumber\]

Світло все ще розходиться, тому зображення віртуальне. Відстань зображення від другої грані становить 1,42 ÷ 0,007 246 = 196 см, а воно зліва від другої грані.

Збільшення товстої лінзи легко знайти. Збільшення, вироблене першим обличчям, є\(C_1/C_2\), як завжди, а потім відбувається подальше збільшення,\(C_3/C_4\) вироблене другим обличчям. Таким чином, загальне збільшення є\(\frac{C_1C_3}{C_2C_4}\), що в цьому випадку становить +3,356. Зображення збільшено в розмірах і воно прямостояче.

Цей метод для товстих лінз також можна використовувати для розділених лінз і дзеркал. Ось один:

Приклад\(\PageIndex{2}\)

На малюнку II.18 показана тонка лінза, відокремлена від дзеркала, і предмет в 14 см від лінзи. Де зображення?

Рішення

\( C_1 = -1/14 = -0.071420 \)см ^-1.

\( C_2 = C_1 +1/25 = -0.031429 \)см ^-1.

\( C_3 = \frac{C_2}{1-40\times C_2}=-0.013924\)см ^-1.

\( C_4 = C_3 + \frac{-2}{-30} =+0.053743\)см ^-1.

Образ реальний. Це 18,96 см зліва від дзеркала. Збільшення становить −0,60. Зображення перевернуто і зменшується.

Звичайно, ті, хто ставить іспити, можуть придумати всілякі неприємні питання. Наприклад, у нас може бути товста лінза і об'єкт, але замість того, щоб нас попросять знайти зображення, нам можуть повідомити відстань зображення і попросити знайти показник заломлення, або товщину, або один з радіусів. Або, що ще гірше, нам можуть не сказати відстань зображення, але нам можуть сказати про його збільшення і чи є воно реальним чи віртуальним, або прямостоячим чи перевернутим, і попросять знайти щось інше. Є безмежні можливості! Ось один.

Показана лінза має радіуси кривизни 16 і 30 см і товщиною 5 см. Об'єкт знаходиться на 36 см ліворуч від грані 16 см. Його зображення знаходиться на 50 см праворуч від 30 см поверхні. Покажіть, що показник заломлення є позитивним рішенням

\(1845n^2 - 2417n - 520 = 0\).

Ось ще один.

Приклад\(\PageIndex{2}\)

Показана лінза має товщину 4 см, а показник заломлення - 1,6. Радіус кривизни першої грані становить 15 см. Об'єкт знаходиться на 32 см ліворуч від 15-сантиметрової грані. Його зображення реальне, перевернуте і збільшене на 22. Визначте радіус кривизни другої грані.

Рішення

Підказки. Образ реальний. З якого боку лінзи знаходиться? Можна легко обчислити\(C_1 , C_2\) і\(C_3\), таким чином, ви повинні мати можливість отримати\(C_4\) від збільшення. Відповідь, до речі, 80,1 см — але чи опукла справа, як показано, чи увігнута праворуч?

Ще один.

Приклад\(\PageIndex{4}\)

Дві лінзи виготовлені з дуже легкого твердого тіла, показник заломлення якого становить лише 1,3. (Я не впевнений, чи є такий матеріал!) і занурюються в рідину з індексом 1,4. Це означає, що опукла лінза розходиться. Друга поверхня другої лінзи - дзеркало, що відбиває. Я вказав радіуси кривизни, а лінзи знаходяться на відстані 40 см один від одного. Паралельне світло йде зліва. Де мова йде про фокус?

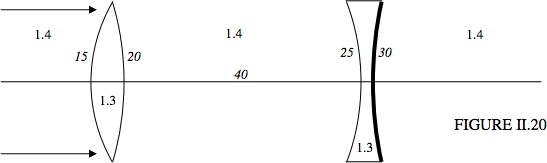
Рішення

Початкова конвергенція\(C_1 = 0\). Я розрахую конвергенцію після того, як світло надходить або залишає кожну поверхню або інтерфейс. Сподіваюся, позначення будуть зрозумілі. Всі сходження знаходяться в см ⁻¹.

\[\begin{align*} C_2 &= 0 + \dfrac{1.3-1.4}{+15} = -0.006. \\[4pt] C_3 &= -0.006 + \dfrac{1.4-1.3}{-20} = -0.0116. \\[4pt] C_4 &= \dfrac{1.4C_3}{1.4-40C_3} = -0.00875.\\[4pt] C_5 &= -0.00875 + \dfrac{1.3-1.4}{-25} = -0.00475.\\[4pt] C_6 &= -0.00475 + \dfrac{-2\times 1.3}{30} =-0.091416. \\[4pt] C_7 &= -0.091416 + \dfrac{1.4-1.3}{+25} = -0.087416.\\[4pt] C_8&=\dfrac{1.4C_7}{1.4-40C_7} = -0.02499319265.\\[4pt] C_9 &= C_8 + \dfrac{1.3-1.4}{-20} = -0.02999319265.\\[4pt] C_{10} &= C_9 + \dfrac{1.4-1.3}{-15} = -0.03665985931. \end{align*}\]

Нарешті\(C_{10} = \frac{1.4}{x}\), так\(x = -38.188 908 15 \left(=-\frac{22035}{577}\right)\) см.

Тобто фокус знаходиться на 38,2 см праворуч від опуклої лінзи, або 1,8 см зліва від увігнутої лінзи.

Вправа\(\PageIndex{1}\)

Складіть задачу, в якій студенту дається фокусна відстань двох лінз, і положення предмета і зображення, а студенту пропонується обчислити відстань між лінзами.