2: Похідні

Last updated

Oct 27, 2022
Save as PDF
- 1.8: Вправи
- 2.1: Властивості похідних

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Похідна функції $f$ - це інша функція $f'$ , визначена як $f'(x) \;\equiv\; \frac{df}{dx} \;\equiv\; \lim_{\delta x \rightarrow 0} \, \frac{f(x + \delta x) - f(x)}{\delta x}.$ Цей вид виразу називається limit expression, оскільки воно передбачає обмеження (в даному випадку межа, де $\delta x$ йде до нуля).

Якщо похідна існує в деякій області $x$ (тобто вищевказаний граничний вираз математично чітко визначено), то ми говоримо, $f$ що диференційовна в цій області. Можна показати, що диференційована функція автоматично безперервна.

Графічно похідна являє собою нахил графіка $f(x)$ , як показано нижче:

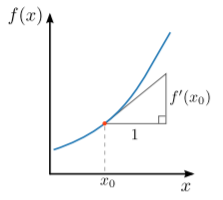
Якщо $f$ диференційовний, ми можемо визначити його похідну другого порядку $f''$ як похідну від $f'$ . Похідні третього порядку і вищого порядку визначаються аналогічно.

2.1: Властивості похідних
2.2: Серія Тейлора
2.3: звичайні диференціальні рівняння
2.4: Часткові похідні
Функції також можуть приймати кілька входів; наприклад, функція f (x, y) відображає два вхідних числа, x і y, і виводить число. Загалом, входи дозволяється варіювати незалежно один від одного. Часткова похідна такої функції є її похідною по відношенню до одного з її входів, зберігаючи інші фіксованими.
2.5: Вправи