8.2: Спотворення простору і часу

7.2.1 Перетворення Лоренца

Відносність говорить про те, що коли два спостерігачі перебувають у різних рамках відліку, кожен спостерігач вважає, що сприйняття часу іншим спотвореним. Ми також побачимо, що щось подібне відбувається з їх спостереженнями відстаней, тому і простір, і час спотворюються. Що саме являє собою це спотворення? Як ми навіть концептуалізуємо це?

Ідея насправді не настільки радикальна, як може здатися спочатку. Ми можемо візуалізувати структуру простору і часу за допомогою графіка з положенням і часом на його осях. Ці графіки вже знайомі, але ми будемо дивитися на них трохи по-іншому. Раніше ми використовували їх для опису руху об'єктів. Сітка, що лежить в основі графіка, була лише сценою, на якій актори грали свої ролі. Тепер фон виходить на перший план: саме час і простір ми вивчаємо. Нам не обов'язково мати лінію або криву, намальовану поверх сітки, щоб представляти конкретний об'єкт. Ми можемо, наприклад, просто захотіти поговорити про події, зображені у вигляді точок на графіку, як на малюнку а.

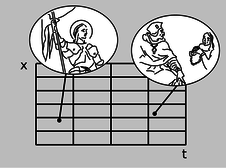
a/Дві події задаються як точки на графіку позиції та часу. Жанна д'Арк допомагає відновити Карла VII на престолі. У більш пізній час і на іншій посаді Жанна д'Арк засуджується до смертної кари.

Спотворення декартової сітки, що лежить в основі графіка, може виникнути з абсолютно звичайних причин, які Ісаак Ньютон охоче прийняв би. Наприклад, ми можемо просто змінити одиниці, що використовуються для вимірювання часу та положення, як на малюнку b.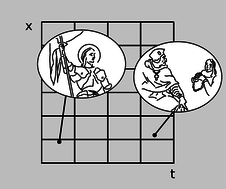

b/Зміна одиниць спотворює a\(x\) -\(t\) графік. На цьому графіку зображені точно такі ж події, як і малюнок а. Єдина зміна полягає в тому, що\(t\) координати\(x\) та вимірюються за допомогою різних одиниць, тому сітка стискається\(t\) та розширюється\(x\).

Ми збираємося мати досить багато прикладів цього типу, так що я прийму конвенцію, показану на малюнку c для їх зображення. Рисунок c узагальнює співвідношення між цифрами a і b в більш компактному вигляді. Сірий прямокутник представляє вихідну координатну сітку фігури a, тоді як сітка чорних ліній представляє нову версію з малюнка b. Опущення сітки з сірого прямокутника полегшує візуальне декодування діаграми.

с/умовність, яку ми будемо використовувати для представлення спотворення часу та простору.

Наша мета розгадати таємниці особливої відносності становить не що інше, як з'ясувати, як намалювати діаграму на зразок c у випадку, коли два різні набори координат представляють вимірювання часу та простору, зроблені двома різними спостерігачами, кожен у русі відносно іншого. Галілей і Ньютон думали, що знають відповідь на це питання, але їх відповідь виявився лише приблизно правильним. Щоб уникнути повторення одних і тих же помилок, нам потрібно чітко прописати те, що, на нашу думку, є основними властивостями часу і простору, які стануть надійною основою для наших міркувань. Хочу підкреслити, що чисто логічного способу прийняття рішення щодо цього переліку властивостей не існує. Ті, які я перерахую, - це просто короткий виклад закономірностей, що спостерігаються в результатах великої кількості експериментів. Крім того, деякі з них є лише приблизними. Наприклад, властивість 1 нижче є лише хорошим наближенням, коли гравітаційне поле слабке, тому це властивість, яка відноситься до спеціальної відносності, а не до загальної відносності.

Експерименти показують, що:

1. Жоден момент часу чи простору не має властивостей, які відрізняють його від будь-якої іншої точки.
2. Так само всі напрямки в просторі мають однакові властивості.
3. Рух відносний, тобто всі інерційні системи відліку однаково дійсні.
4. Причинність тримається в сенсі, описаному на сторінці 381.
5. Час залежить від стану руху спостерігача.

Більшість з них не дуже підривні. Властивості 1 і 2 датуються тим часом, коли Галілей і Ньютон почали застосовувати однакові універсальні закони руху до Сонячної системи і до землі; це суперечило Аристотелю, який вважав, що, наприклад, скеля, природно, захоче рухатися в певному особливому напрямку (вниз), щоб досягти певне особливе місце розташування (земна поверхня). Властивість 3 є причиною того, що Ейнштейн назвав свою теорію «відносністю», але Галілей і Ньютон вважали, що це точно так само, як інсценовано обкаткою Галілея з Церквою над питанням про те, чи дійсно земля може бути в русі навколо Сонця. Властивість 4, ймовірно, здивує більшість людей лише тому, що вона стверджує таким слабким і спеціалізованим чином те, що вони відчувають глибоко, має бути правдою. Єдиний дійсно дивний пункт у списку - 5, але експеримент Хафеле-Кітінга змушує це на нас.

d/Галілейська версія зв'язку між двома рамками відліку. Як і у всіх таких графіках у цьому розділі, вихідні координати, представлені сірим прямокутником, мають вісь часу, яка йде вправо, і вісь положення, яка йде прямо вгору.

Якби не властивість 5, ми могли б уявити, що цифра d дасть правильне перетворення між рамками відліку в русі відносно один одного. Припустимо, що спостерігач 1, сітка якого збігається з сірим прямокутником, є автостопом, що стоїть біля дороги. Подія А - це крапля дощу, що б'є головою, а подія B - ще одна крапля дощу, що б'є голову. Він каже, що A і B відбуваються в одному місці в просторі. Спостерігач 2 - автомобіліст, який проїжджає повз без зупинки; йому пасажирський салон його автомобіля знаходиться в стані спокою, в той час як асфальт ковзає по низу. Він каже, що А і В відбуваються в різних точках простору, тому що за час між першою краплею дощу і другою автостоп перемістився назад. З іншого боку, спостерігач 2 каже, що події А і С відбуваються в одному місці, в той час як автостопом не погоджується. Нахил сітки-ліній - це просто швидкість відносного руху кожного спостерігача щодо іншого.

Малюнок d має звичну, втішну і надзвичайно розумну поведінку, але вона також буває неправильною, оскільки порушує майно 5. Спотворення координатної сітки лише перемістило вертикальні лінії вгору і вниз, тому обидва спостерігачі погоджуються, що події, такі як B і C, є одночасними. Якби це було дійсно так, як все працювало, то всі спостерігачі могли синхронізувати всі свої годинники один з одним раз і назавжди, і годинник ніколи не вийшли з синхронізації. Це суперечить результатам експерименту Хафеле-Кітінга, в якому всі три годинника спочатку були синхронізовані у Вашингтоні, але пізніше вийшли з ладу через їх різних станів руху.

Може здатися, що у нас все ще була величезна кількість місця для похитування, доступних для правильної форми спотворення. Виявляється, однак, що властивостей 1-5 достатньо, щоб довести, що існує лише одна відповідь, яка знайдена Ейнштейном у 1905 році. Щоб зрозуміти, чому це так, давайте попрацюємо процесом усунення.

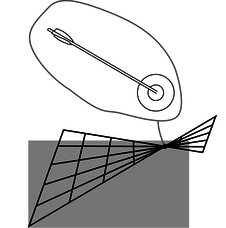
e/Трансформація, яка призводить до розбіжностей щодо того, чи відбуваються дві події одночасно і в одному місці. Це не просто питання думки. Або стрілка потрапила в яблучко, або це не так.

На малюнку е показано перетворення, яке може здатися на перший погляд таким же хорошим кандидатом, як і будь-який інший, але це порушує властивість 3, що рух є відносним, з наступної причини. У системі відліку спостерігача 2 деякі лінії сітки перетинають один одного. Це означає, що спостерігачі 1 і 2 не погоджуються з тим, чи є певні події однаковими. Наприклад, припустимо, що подія A позначає прибуття стрілки в яблучко цілі, а подія B - це місце і час, коли бичаче око пробивається. Події A і B відбуваються в одному місці і одночасно. Якщо один спостерігач каже, що A і B збігаються, а інший каже, що ні, ми маємо пряме протиріччя. Оскільки дві системи відліку на малюнку e дають суперечливі результати, одна з них правильна, а одна - неправильна. Це порушує властивість 3, тому що всі інерційні системи відліку повинні бути однаково дійсними. Щоб уникнути подібних проблем, ми чітко повинні переконатися, що жодна з ліній сітки ніколи не перетинає один одного.

Наступний тип перетворення, який ми хочемо убити, показаний на малюнку f, в якому лінії сітки криві, але ніколи не перетинають один одного. Біда з цим полягає в тому, що він порушує властивість 1, рівномірність часу і простору. Трансформація незвично «звивиста» при А, тоді як у B набагато більш плавна. Це не може бути правильним, оскільки перетворення повинно залежати лише від відносного стану руху двох систем відліку, і ця інформація не виділяє особливої ролі для будь-якої конкретної точки простору-часу. Якби, наприклад, у нас був один кадр відліку, що обертається відносно іншого, то навколо осі обертання було б щось особливе. Але ми говоримо тільки про інерційні системи відліку тут, як зазначено в властивості 3, так що ми не можемо мати обертання; кожен кадр відліку повинен рухатися по прямій лінії з постійною швидкістю. Для кадрів, пов'язаних таким чином, немає нічого, що могло б виділити таку подію, як A для спеціального лікування порівняно з B, тому перетворення f порушує властивість 1.

Приклади на малюнках e та f показують, що трансформація, яку ми шукаємо, повинна бути лінійною, тобто вона повинна перетворювати лінії в лінії, а крім того, що вона повинна приймати паралельні лінії до паралельних ліній. Ейнштейн писав у своїй роботі 1905 року, що «... зважаючи на властивість однорідності [властивість 1], яку ми приписуємо часу та простору, [перетворення] має бути лінійним». ¹ Застосовуючи це до наших діаграм, вихідний сірий прямокутник, який є особливим типом паралелограма, що містить прямі кути, повинен бути перетворений в інший паралелограм. Існує три типи перетворень, цифра g, які мають цю властивість. Справа I - це галілейське перетворення фігури d на сторінці 386, яке ми вже виключили.

g/ Три типи перетворень, що зберігають паралелізм. Їх відмінною рисою є те, що вони роблять з одночасністю, як показано тим, що відбувається з лівим краєм вихідного прямокутника. У I лівий край залишається вертикальним, тому одночасні події залишаються одночасними. У II лівий край повертається проти годинникової стрілки. У III він повертається за годинниковою стрілкою.

Випадок II також можна відкинути. Тут кожна точка на сітці обертається проти годинникової стрілки. Який фізичний параметр визначав би величину обертання? Єдине, що могло б бути актуальним\(v\), це відносна швидкість руху двох систем відліку по відношенню один до одного. Але якби кут повороту був пропорційний\(v\), то при досить великих швидкостях сітка мала б ліву і праву зворотну сторону, і це порушило б властивість 4, причинність: один спостерігач сказав би, що подія А викликала більш пізню подію B, але інший спостерігач сказав би, що Б прийшов першим і викликав A.

h/У одиницях, найбільш зручних для відносності, перетворення має симетрію близько 45-градусної діагональної лінії.

Єдина можливість, що залишилася - це випадок III, який я перемалював на малюнку h з парою змін. Це той, який Ейнштейн передбачив у 1905 році. Трансформація відома як трансформація Лоренца після ХендріКлоренца (1853-1928), який частково передбачив роботу Ейнштейна, не дійшовши до правильної інтерпретації. Спотворення - це своєрідне згладжування і розтягування, як це передбачають руки. Крім того, ми вже бачили на малюнках a - c на сторінці 385, що ми вільні розтягувати або стискати все стільки, скільки нам подобається в горизонтальному і вертикальному напрямках, тому що це просто відповідає вибору різних одиниць вимірювання часу і відстань. На малюнку h я вибрав одиниці, які надають всьому малюнку зручну симетрію близько 45-градусної діагональної лінії. Зазвичай не має сенсу говорити про кут 45 градусів на графіку, осі якого мали різні одиниці. Але в теорії відносності симетричний вигляд трансформації говорить нам, що простір і час повинні розглядатися на одній основі і вимірювати в одних і тих же одиницях.

i/Інтерпретація перетворення Лоренца. Нахил, зазначений на малюнку, дає відносну швидкість двох систем відліку. Події A та B, які були одночасними у кадрі 1, не є одночасними у кадрі 2, де подія A відбувається праворуч від\(t=0\) лінії, представленої лівим краєм сітки, але подія B відбувається зліва від неї.

Як і в нашому обговоренні перетворення Галілея, схили трактуються як швидкості, а нахил навкологоризонтальних ліній на малюнку i інтерпретується як відносна швидкість двох спостерігачів. Різниця між галілейською версією та релятивістською полягає в тому, що зараз відбувається згладжування і з іншого боку. Лінії, які були вертикальними в оригінальній сітці, представляючи одночасні події, тепер нахиляються вправо. Це говорить нам про те, що, як того вимагає майно 5, різні спостерігачі не погоджуються з тим, чи є події, що відбуваються в різних місцях, одночасними. Експеримент Хафеле-Кітінга говорить нам, що цей ефект неодночасності досить малий, навіть коли швидкість така ж велика, як швидкість пасажирського літака, і це те, що ми очікували б за принципом відповідності. Спосіб, який це виражається в графіку, полягає в тому, що якщо ми виберемо одиницю часу, щоб бути другою, то одиниця відстані виявляється сотні тисяч миль. У цих одиницях швидкість пасажирського реактивного літака надзвичайно мала, тому нахил на\(v\) малюнку i надзвичайно малий, а кількість спотворень крихітна - це було б занадто мало, щоб побачити на цьому масштабі.

Єдине, що залишилося визначити про перетворення Лоренца - це розмір перетвореного паралелограма щодо розміру вихідного. Хоча креслення рук на малюнку h може припустити, що сітка деформується як каркас з жорсткої дроту для вішалки, це не так. Якщо ви уважно подивитеся на фігуру, то побачите, що краї згладженого паралелограма насправді трохи довші, ніж краю вихідного прямокутника. Насправді те, що залишається однаковим, це не довжини, а області, як доведено в підписі до малюнка j.

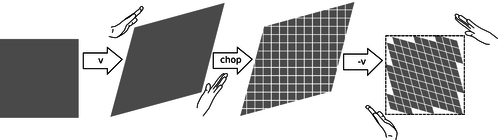
j/ Доказ того, що перетворення Лоренца не змінюють площу: ми спочатку піддаємо квадрат перетворенню зі швидкістю\(v\), і це збільшує його площу в коефіцієнт\(R(v)\), який ми хочемо довести дорівнює 1. Ми подрібнюємо отриманий паралелограм на маленькі квадрати і, нарешті, застосовуємо\(-v\) перетворення; це змінює площу кожного маленького квадрата на коефіцієнт\(R(-v)\), тому площа всієї фігури також масштабується\(R(-v)\). Кінцевим результатом є відновлення квадрату первісної форми і площі, так що\(R(v)R(-v)=1\). Але\(R(v)=R(-v)\) за властивістю 2 spacetime на сторінці 385, де зазначено, що всі напрямки в просторі мають однакові властивості, так\(R(v)=1\).

7.2.2\(\gamma\) Коефіцієнт

Маючи невелику алгебру та геометрію (домашнє завдання 7, стор. 439), можна використовувати властивість equal-area, щоб показати, що коефіцієнт\(\gamma\) (грецька буква гамма), визначений на малюнку k, задається рівнянням

\[\begin{equation*} \gamma = \frac{1}{\sqrt{1-v^2}} . \end{equation*}\]

Якщо ви добре навчалися фізиці, перше, що ви, мабуть, думаєте, коли дивитеся на це рівняння, це те, що це повинно бути нісенітницею, тому що його одиниці не мають сенсу. Як ми можемо взяти щось з одиницями швидкості в квадраті, і відняти його від безстрокового 1? Але пам'ятайте, що це виражається в наших особливих релятивістських одиницях, в яких одні і ті ж одиниці використовуються для відстані і часу. У цій системі швидкості завжди безроздільні. Подібні речі часто трапляються у фізиці. Наприклад, до того, як Джеймс Джоуль виявив збереження енергії, ніхто не знав, що теплова та механічна енергія - це різні форми одного і того ж, тому замість того, щоб вимірювати їх обидва в одиницях джоулів, як ми це зробили б зараз, вони вимірювали тепло в одній одиниці (наприклад, калорії) та механічну енергію в іншій (така як фут-фунти). У звичайних метричних одиницях нам просто потрібен додатковий коефіцієнт перетворення\(c\), і рівняння стає

\[\begin{equation*} \gamma = \frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}} . \end{equation*}\]

Ось чому ми дбаємо про це\(\gamma\). Малюнок k визначає його як співвідношення двох разів: час між двома подіями, вираженими в одній системі координат, і час між тими ж двома подіями, що вимірюються в іншій. Тлумачення таке:

k/\(\gamma\) Коефіцієнт.

Дилатація часу

Годинник працює найшвидше в рамках відліку спостерігача, який знаходиться в стані спокою щодо годинника. Спостерігач в русі щодо тактової частоти\(v\) сприймає годинник як біжать повільніше в рази\(\gamma\).

Як доведено на цифрах l і m, довжини також спотворюються:

l/Лінійка рухається в кадрі 1, представленому квадратом, але в спокої в кадрі 2, показаний у вигляді паралелограма. Кожна фотографія лінійки - це знімок, зроблений у певний момент, як судять за поняттям одночасності кадру 2. Спостерігач у кадрі 1 оцінює довжину лінійки замість цього відповідно до визначення одночасності кадру 1, тобто за допомогою точок, які вибудовуються вертикально на графіку. Лінійка виглядає коротше в кадрі, в якому вона рухається. Як доведено на малюнку m, довжина стискається від\(L\) до\(L/\gamma\).

m/Ця цифра доводить, як стверджується на малюнку l, що скорочення довжини дорівнює\(x=1/\gamma\). Спочатку нарізаємо паралелограм вертикально, як салямі, і скочуємо скибочки вниз, роблячи верхній і нижній краю горизонтальними. Потім те ж саме робимо в горизонтальному напрямку, формуючи прямокутник зі сторонами\(\gamma\) і\(x\). Оскільки і перетворення Лоренца, і процеси нарізки залишають області незмінними, площа\(\gamma x\) прямокутника повинна дорівнювати площі вихідного квадрата, яка дорівнює 1.

скорочення довжини

Метр-палиця здається найдовшою спостерігачеві, який перебуває у спокої щодо неї. Спостерігач, що рухається відносно метрової палиці,\(v\) спостерігає за палицею, яку потрібно вкоротити в рази\(\gamma\).

Вправа\(\PageIndex{1}\)

Що таке\(\gamma\) коли\(v=0\)? Що це означає?

(відповідь у зворотному боці PDF-версії книги)

Приклад\(\PageIndex{1}\): An interstellar road trip

Аліса залишається на землі, поки її близнюк Бетті вирушає на космічному кораблі для Тау Кеті, сусідньої зірки. Тау Кеті знаходиться на відстані 12 світлових років, тому, хоча Бетті подорожує на 87% швидкості світла, їй знадобиться багато часу, щоб дістатися туди: 14 років, за словами Аліси.

n/Приклад 1.

Бетті відчуває розширення часу. На такій швидкості вона\(\gamma\) дорівнює 2.0, так що плавання здасться їй лише 7 років. Але існує ідеальна симетрія між рамками відліку Аліси та Бетті, тому Бетті погоджується з Алісою щодо їх відносної швидкості; Бетті бачить себе як в спокої, тоді як сонце і Тау Кеті обидва рухаються назад на 87% швидкості світла. Як же тоді вона може спостерігати Тау Цеті, щоб дістатися до неї всього за 7 років, коли потрібно 14 років, щоб проїхати 12 світлових років з такою швидкістю?

Потрібно враховувати скорочення довжини. Бетті бачить, що відстань між сонцем і Тау Кеті скорочується в 2 рази. Те ж саме відбувається з Алісою, яка спостерігає за Бетті та її космічним кораблем, щоб передбачити.

Приклад\(\PageIndex{2}\): Large time dilation

Ефект розширення часу в експерименті Хафеле-Кітінга був дуже невеликим. Якщо ми хочемо побачити великий ефект розширення часу, ми не можемо зробити це з чимось розміром атомного годинника, який вони використовували; кінетична енергія була б більшою, ніж загальний мегатоннаж усіх світових ядерних арсеналів. Однак ми можемо прискорити субатомні частинки до швидкості, з якою\(\gamma\) велика. Для експериментальних фізиків частинок відносність - це те, що ви робите цілий день, перш ніж відправитися додому і зупинитися в магазині за молоком. Ранній, низькоточний експеримент такого роду був проведений Россі і Холлом в 1941 році, використовуючи природні космічні промені. На малюнку р показано експеримент 1974 року ² подібного типу, який перевіряв розширення часу, передбачене відносністю, з точністю близько однієї частини на тисячу.

Частинки\(\mu\), звані мюонами (названі на честь грецької літери «myoo»), вироблялися прискорювачем в ЦЕРН, недалеко від Женеви. Мюон - це, по суті, важча версія електрона. Мюони зазнають радіоактивного розпаду, триваючи в середньому лише 2.197,\(\mu\text{s}\) перш ніж вони випаровуються в електрон і два нейтрино. Експеримент 1974 року був фактично побудований для того, щоб виміряти магнітні властивості мюонів, але він зробив високоточний тест розширення часу як побічний продукт. Оскільки мюони мають такий же електричний заряд, як електрони, їх можна захопити за допомогою магнітних полів. Мюони вводили в кільце, показане на малюнку р, кружляли навколо нього, поки вони не зазнали радіоактивного розпаду. На швидкості, з якою рухалися ці мюони, вони мали\(\gamma=29.33\), тому в середньому вони тривали в 29,33 рази довше звичайного терміну служби. Іншими словами, вони були як крихітні будильники, які самознищувалися в випадково обраний час. На малюнку o показано кількість підрахованих радіоактивних розпадів в залежності від часу, що минув після того, як даний потік мюонів був введений в кільце для зберігання. Дві пунктирні лінії показують швидкості розпаду, передбачені з відносністю та без неї. Релятивістська лінія - це та, яка погоджується з експериментом.

o/Мюони прискорюються майже\(c\) зазнають радіоактивного розпаду набагато повільніше, ніж вони, за словами спостерігача в спокої щодо мюонів. Перші дві точки даних (незаповнені кола) були схильні до великих систематичних помилок.

p/Апарат, що використовується для перевірки релятивістського розширення часу, описаного в прикладі 2. Видатні чорно-білі блоки - це великі магніти, що оточують круглу трубу з вакуумом всередині. (c) 1974 року ЦЕРН.

Приклад\(\PageIndex{3}\): An example of length contraction

На малюнку q показано рендеринг художником скорочення довжини для зіткнення двох золотих ядер з релятивістськими швидкостями в прискорювачі RHIC в Лонг-Айленді, штат Нью-Йорк, який вийшов на лінію в 2000 році. Золоті ядра виглядали б майже сферичними (або трохи подовженими, як американський футбол) у кадрах, що рухаються разом з ними, але в кадрі лабораторії вони обидва виглядають різко передбаченими, коли вони наближаються до точки зіткнення. На пізніших знімках зображені ядра, що зливаються, утворюючи гарячий суп, в якому експериментатори сподіваються спостерігати нову форму речовини.

q/ Зіткнення ядер показують релятивістське скорочення довжини.

Приклад\(\PageIndex{1}\): The garage paradox

Один з найвідоміших з усіх так званих парадоксів відносності пов'язаний з нашим неправильним почуттям, що одночасність чітко визначена. Ідея полягає в тому, що можна було б взяти шкільний автобус і загнати його на релятивістських швидкостях в гараж звичайного розміру, в який він нормально не помістився б. Через скорочення довжини автобус нібито поміститься в гаражі. Водій, однак, сприйматиме гараж як контракт і, таким чином, ще менш здатний утримувати автобус.

Парадокс вирішується, коли ми визнаємо, що концепція примірки автобуса в гаражі «все відразу» містить приховане припущення, припущення, що має сенс запитати, чи може передня і задня частина автобуса одночасно перебувати в гаражі. Спостерігачі в різних системах відліку, що рухаються з високою відносною швидкістю, не обов'язково погоджуються, чи відбуваються речі одночасно. Як показано на малюнку r, людина в рамі гаража може закрити двері в одну мить В, він сприймає як одночасне з приходом переднього бампера А на задню стінку гаража, але водій не погодився б про одночасність цих двох подій, і сприймав би двері як мають закрилася довго після того, як вона переорана через задню стінку.

r/Приклад 4: У системі відліку гаража автобус рухається, і може поміститися в гаражі через його скорочення довжини. У системі відліку автобуса гараж рухається, і не може утримувати автобус через його скорочення довжини.

7.2.3 Універсальна швидкість\(c\)

Давайте трохи більше подумаємо про роль 45-градусної діагоналі в перетворенні Лоренца. Нахили на цих графіках інтерпретуються як швидкості. Ця лінія має нахил 1 в релятивістських одиницях, але цей нахил відповідає\(c\) звичайним метричним одиницям. Ми вже знаємо, що одиниця релятивістської відстані повинна бути надзвичайно великою порівняно з релятивістською одиницею часу, тому\(c\) повинна бути надзвичайно великою. Тепер зверніть увагу, що відбувається, коли ми виконуємо трансформацію Лоренца: ця конкретна лінія розтягується, але нова версія лінії лежить прямо поверх старої, а її нахил залишається таким же. Іншими словами, якщо один спостерігач каже, що щось має швидкість, рівну\(c\), кожен інший спостерігач також погодиться з цією швидкістю. (Те ж саме відбувається з\(-c\).)

Швидкості не просто додавати і віднімати.

Це контрінтуїтивно, оскільки ми очікуємо, що швидкості додаватимуться та віднімаються у відносному русі. Якщо собака тікає від мене зі швидкістю 5 м/с щодо тротуару, а я бігаю за ним зі швидкістю 3 м/с, швидкість собаки в моїй рамці відліку 2 м/с За всім, що ми дізналися про рух, собака повинна мати різну швидкість в двох кадрах: 5 м/с в рамі тротуару і 2 м/с в моєму. Але швидкості вимірюються діленням відстані на час, і відстань і час спотворюються релятивістськими ефектами, тому ми насправді не повинні очікувати, що звичайне арифметичне додавання швидкостей буде триматися в відносності; це наближення, яке діє при малих швидкостях порівняно з \(c\).

Універсальне обмеження швидкості

Наприклад, припустимо, Джанет здійснює подорож на космічному кораблі, і розганяється, поки вона не рухається\(0.6c\) відносно землі. Потім вона запускає космічний зонд у прямому напрямку зі швидкістю відносно свого корабля\(0.6c\). Ми можемо подумати, що зонд тоді рухався зі швидкістю\(1.2c\), але насправді відповідь все ще менше\(c\) (проблема 1, стор. 438). Це приклад більш загального факту про відносність, який полягає в тому, що\(c\) являє собою універсальне обмеження швидкості. Цього вимагає причинно-наслідковий зв'язок, як показано на малюнку s.

s/Доказ того, що причинно-наслідковий зв'язок накладає універсальне обмеження швидкості. У вихідному кадрі відліку, представленому квадратом, подія A відбувається трохи раніше події B. У новому кадрі, показаному паралелограмом\(t=0\), A відбувається після, але B відбувається раніше\(t=0\); тобто B відбувається до А. Час впорядкування двох подій було змінено. Це може статися тільки тому, що події A і B дуже близькі між собою в часі і досить далеко один від одного в просторі. Відрізок лінії, що з'єднує A і B, має нахил більше 1, що означає, що якщо ми хотіли бути присутніми на обох подіях, нам доведеться подорожувати зі швидкістю, більшою за\(c\) (що дорівнює 1 в одиницях, використовуваних на цьому графіку). Ви побачите, що якщо ви виберете будь-які дві точки, для яких нахил відрізка лінії, що з'єднує їх, менше 1, ви ніколи не зможете змусити їх перетинати нову\(t=0\) лінію цим смішним, зворотним часом способом. Оскільки різні спостерігачі не погоджуються щодо часового порядку подій, таких як A та B, причинність вимагає, щоб інформація ніколи не подорожувала від А до Б або від B до A; якби це сталося, то у нас були б парадокси подорожей у часі. Висновок полягає в тому, що\(c\) це максимальна швидкість причинно-наслідкового впливу в відносності.

т/Експеримент Майкельсона-Морлі, показаний на фотографіях, і малюнки з оригінального паперу 1887 р. Спрощений креслення апарату. Промінь світла від джерела, s, частково відбивається і частково передається напівпосрібленим дзеркалом\(\text{h}_1\). Дві частини напівінтенсивності променя відбиваються дзеркалами в a і b, возз'єдналися і спостерігаються в телескопі, т Якби земна поверхня повинна була рухатися через ефір, то час, прийнятий двома світловими хвилями для проходження через рухомий ефір, було б нерівним, і отриманий час відставання можна виявити, спостерігаючи перешкоди між хвилями, коли вони возз'єдналися. У реальному апараті світлові промені відбивалися неодноразово. Ефективна довжина кожної руки була збільшена до 11 метрів, що значно покращило його чутливість до невеликої очікуваної різниці швидкості світла. У більш ранній версії експерименту вони зіткнулися з проблемами з його «надзвичайною чутливістю до вібрації», яка була «настільки великою, що неможливо було побачити інтерференційні смуги, крім коротких інтервалів... навіть о другій годині ранку». Тому вони встановили все це на масивному камені, що плаває в басейні ртуті, що також дозволило легко обертати його. Фото апарату.

Світло подорожує в\(c\).

Тепер розглянемо промінь світла. Ми звикли говорити випадково про «швидкість світла», але що це насправді означає? Рух є відносним, тому зазвичай, якщо ми хочемо говорити про швидкість, ми повинні вказати, що він вимірюється відносно. Звукова хвиля має певну швидкість щодо повітря, а водяна хвиля має свою швидкість щодо води. Наприклад, якщо ми хочемо виміряти швидкість океанської хвилі, ми повинні обов'язково виміряти її в системі відліку в спокої щодо води. Але світло - це не вібрація фізичного середовища; воно може поширюватися через майже ідеальний вакуум космічного простору, як коли промені сонячного світла рухаються на землю. Це здається парадоксом: світло повинен мати певну швидкість, але немає можливості вирішити, в якій системі відліку його виміряти. Вихід з парадоксу полягає в тому, що світло повинен рухатися зі швидкістю, рівною\(c\). Оскільки всі спостерігачі погоджуються на швидкості\(c\), незалежно від їх системи відліку, все узгоджено.

Експеримент Майкельсона-Морлі

Сталість швидкості світла насправді вже спостерігалася, коли Ейнштейн був 8-річним хлопчиком, але оскільки ніхто не міг зрозуміти, як її інтерпретувати, результат значною мірою ігнорувався. У 1887 році Майкельсон і Морлі створили розумний апарат для вимірювання будь-якої різниці в швидкості світлових променів, що рухаються схід-захід і північ-південь. Рух землі навколо Сонця на 110 000 км/год (близько 0,01% від швидкості світла) припадає на наш захід протягом дня. Майкельсон і Морлі вважали, що світло - це вібрація загадкового середовища під назвою ефір, тому вони очікували, що швидкість світла буде фіксованою величиною щодо ефіру. Коли земля рухалася через ефір, вони думали, що будуть спостерігати вплив на швидкість світла вздовж лінії схід-захід. Наприклад, якщо вони випустили промінь світла в західному напрямку протягом дня, вони очікували, що він віддалиться від них з меншою, ніж звичайна швидкість, оскільки земля переслідувала його через ефір. Вони були здивовані, коли виявили, що очікуваного 0.01% зміни швидкості світла не відбулося.

Приклад\(\PageIndex{4}\): The ring laser gyroscope

Якщо ви літали в реактивному літаку, ви можете подякувати відносності за допомогу вам уникнути врізки в гору або океан. На малюнку u показаний стандартний шматок навігаційного обладнання, який називається кільцевим лазерним гіроскопом. Промінь світла розбивається на дві частини, направляється по периметру приладу, і возз'єднується. Оскільки швидкість світла постійна, ми очікуємо, що дві частини повернуться разом одночасно. Якщо вони цього не роблять, це докази того, що пристрій обертається. Комп'ютер літака відчуває це і зазначає, скільки обертання накопичилося.

u/кільцевий лазерний гіроскоп.

Приклад\(\PageIndex{6}\): No frequency-dependence

Відносність має тільки одну універсальну швидкість, тому вона вимагає, щоб всі світлові хвилі рухалися з однаковою швидкістю, незалежно від їх частоти і довжини хвилі. В даний час найкращі експериментальні випробування інваріантності швидкості світла щодо довжини хвилі походять від астрономічних спостережень гамма-сплеску, які є раптовими виливами високочастотного світла, які, як вважають, походять від вибуху наднової в іншій галактиці. Одне з таких спостережень, в 2009 році, ³ виявило, що часи прибуття всіх різних частот в сплеску відрізнялися не більше ніж на 2 секунди із загального часу в польоті близько десяти мільярдів років!

Питання для обговорення

◊ Людина в космічному кораблі, що рухається зі швидкістю 99.999999% світла щодо Землі, світить ліхтариком вперед через запилене повітря, тому промінь видно. Що вона бачить? Як би це виглядало спостерігачеві на Землі?

◊

Дискусійне питання B.

Питання, з яким часто борються студенти, полягає в тому, чи дійсно час і простір можуть бути спотворені, чи це просто здається таким чином. Порівняйте з оптичними ілюзіями або фокусами. Як ви могли переконатися, наприклад, що лінії на малюнку насправді паралельні? Релятивістські ефекти однакові чи ні?

◊ На космічному кораблі, що рухається з релятивістськими швидкостями, лекція здавалася б ще довшою і нуднішою, ніж зазвичай?

◊ Механічні годинники можуть впливати на рух. Наприклад, це було значним технологічним досягненням побудувати годинник, який міг плисти на борту корабля і все ще зберігати точний час, дозволяючи визначити довготу. Чим це схоже на релятивістське розширення часу або відрізняється від нього?

◊ Малюнок q зі сторінки 392, що зображує зіткнення двох ядер на прискорювачі RHIC, відтворюється нижче. Як виглядатимуть форми двох ядер для мікроскопічного спостерігача, що їде на лівому ядрі? Спостерігачу, що їде на правій руці? Чи можуть вони домовитися про те, що відбувається? Якщо ні, то чому б і ні - врешті-решт, вони не повинні бачити те ж саме, якщо вони обидва порівнюють два ядра пліч-о-пліч в один і той же момент часу?

v/Дискусійне питання Е: зіткнення ядер показують релятивістське скорочення довжини.

◊ Якщо ви приклеїте шматок поролону у вікно свого автомобіля під час руху по автостраді, вітер може трохи стиснути його. Чи має сенс інтерпретувати релятивістське скорочення довжини як тип деформації, яка штовхає атоми об'єкта разом, як це? Як це пов'язано з дискусійним питанням Е?

◊ Кулеметник на малюнку розсилає бризки куль. Припустимо, що кулі стріляють в космічний простір, і що пройдені відстані складають трильйони миль (щоб людська фігура на схемі не масштабувалася). Після довгого часу кулі досягають точок, показаних крапками, які знаходяться однаково далеко від гармати. Їх прибуття в ті точки - це події від А до Е, які відбуваються в різний час. Ланцюг ударів поширюється по всьому простору зі швидкістю, більшою ніж\(c\). Чи порушує це особлива відносність?

Дискусійне питання G.

7.2.4 Відсутність дій на відстані

Ньютонівська картина

Ньютонівська картина Всесвіту має частинки, які взаємодіють один з одним, докладаючи сили на відстані, і ці сили, як представляється, відбуваються без затримки часу. Наприклад, припустимо, що надпотужні інопланетяни, розлючені, коли чують музику диско в наших радіопередачах AM, приходять в нашу Сонячну систему з місією очистити Всесвіт від нашого естетичного забруднення. Вони прикладають силу до нашого сонця, змушуючи його вилітати з Сонячної системи на мільйон миль на годину. Згідно із законами Ньютона, гравітаційна сила Сонця на землі відразу ж почне падати. Це буде виявлено на землі, і оскільки сонячному світлу потрібно вісім хвилин, щоб дістатися від сонця до землі, зміна сили тяжіння, на думку Ньютона, стане першим способом, яким земляни дізнаються погані новини - сонце не почне помітно відступати лише трохи пізніше. Хоча цей сценарій вигадливий, він показує реальну особливість законів Ньютона: що інформація може передаватися з одного місця у Всесвіті в інше з нульовою затримкою часу, так що передача і прийом відбуваються точно в один і той же момент. Ньютон був досить гострим, щоб зрозуміти, що це вимагало нетривіального припущення, яке полягало в тому, що існує якийсь цілком об'єктивний і чітко визначений спосіб сказати, чи відбулися дві речі точно в один і той же момент. Він висловив це припущення прямо: «Абсолютне, істинне, і математичне час, само по собі, і від власної природи тече з постійною швидкістю, не зважаючи ні на що зовнішнє...»

Часові затримки сил, що чинилися на відстані

Відносність забороняє миттєву дію Ньютона на відстані. Бо припустимо, що миттєва дія на відстані існувала. Тоді можна було б надсилати сигнали з одного місця у Всесвіті в інше без будь-яких затримок у часі. Це дозволило б ідеально синхронізувати всі годинники. Але експеримент Хафела-Кітінга демонструє, що годинник A і B, які були спочатку синхронізовані, будуть дрейфувати з синхронізації, якщо один знаходиться в русі відносно іншого. При миттєвій передачі сигналів ми могли визначити, не чекаючи возз'єднання A і B, які були попереду і які були позаду. Оскільки їх не потрібно возз'єднувати, не потрібно піддаватися жодному прискоренню; кожен годинник може фіксувати інерційну систему відліку з вектором швидкості, який не змінює ні свого напрямку, ні його величини. Але це порушує принцип, що постійно-швидкісний рух є відносним, адже кожен годинник можна вважати перебувати в стані спокою, у власній системі відліку. Оскільки жоден експеримент ніколи не виявляв жодного порушення відносності руху, робимо висновок, що миттєве дію на відстані неможливо.

Оскільки сили не можуть передаватися миттєво, стає природним уявити силові ефекти, що поширюються назовні від їхнього джерела, як брижі на ставку, і тоді у нас немає іншого вибору, як призначити ці брижі деяку фізичну реальність. Ми називаємо їх полями, і вони мають своє самостійне існування. Гравітація передається через поле, яке називається гравітаційним полем. Крім гравітації, є й інші основні поля сили, такі як електрика та магнетизм (гл. 10 - 11). Брижі електричного і магнітного полів виявляються світловими хвилями. Це говорить нам про те, що швидкість, з якою поширюються брижі електричного та магнітного поля\(c\), повинна бути, і аргументом, подібним до тієї, що в підрозділі 7.2.3, повинна триматися для будь-якого іншого фундаментального поля, включаючи гравітаційне поле.

Поля не повинні похитуватися; вони можуть триматися нерухомо, а також. Наприклад, магнітне поле Землі майже постійне, тому ми можемо використовувати його для визначення напрямку.

Навіть порожній простір, значить, не є абсолютно безликим. Він має вимірювані властивості. Наприклад, ми можемо скинути скелю для того, щоб виміряти напрямок гравітаційного поля, або використовувати магнітний компас, щоб знайти напрямок магнітного поля. Ця концепція справила глибоке враження на Ейнштейна в дитинстві. Він нагадав, що в п'ятирічному віці дар магнітного компаса переконав його, що за речами є «щось, щось глибоко приховане».

Ще більше доказів того, що силові поля реальні: вони несуть енергію.

ж/Поля несуть енергію.

Аргумент куріння гармати для цього дивного поняття подорожі сили брижі походить від того, що вони несуть енергію. На малюнку х /1 Аліса і Бетті тримають кулі A і B на деякій відстані один від одного. Ці кулі створюють силу один на одного; насправді не має значення заради нашого аргументу, чи є ця сила гравітаційною, електричною чи магнітною. Скажімо, це електричне, тобто, що кульки мають такий електричний заряд, який іноді змушує ваші шкарпетки чіплятися, коли вони виходять з сушарки для білизни. Ми скажемо, що сила відразлива, хоча знову ж таки це не має значення.

x/Обговорення питання E.

Якщо Аліса вирішить перемістити свою м'яч ближче до Бетті, х /2, Алісі доведеться виконати механічну роботу проти електричного відштовхування, спалюючи частину калорій від того шоколадного чізкейка, який вона мала в обід. Це зниження хімічної енергії її організму компенсується відповідним збільшенням енергії електричної взаємодії. Мало того, але Аліса відчуває, що опір жорсткіше, коли кулі зближуються і відштовхування посилюється. Їй доводиться робити трохи зайвої роботи, але це все правильно враховується при взаємодії енергія.

Але тепер припустимо, х /3, що Бетті вирішує зіграти трюк над Алісою, кинувши B далеко так само, як Аліса готується рухатися А. Ми вже встановили, що Аліса не може відчути рух Б миттєво, тому електричні сили повинні фактично поширюватися електричним полем. Звичайно, цей експеримент є абсолютно непрактичним, але припустимо, заради аргументу, що час, який потребує зміни електричного поля для поширення по діаграмі, досить довгий, щоб Аліса могла завершити свій рух, перш ніж вона відчує ефект зникнення Б. Вона все ще отримує несвіжу інформацію про позицію Б. Коли вона рухається A вправо, вона відчуває відштовхування, тому що поле в її області простору все ще є полем, викликаним B в його старому положенні. Вона спалила деякі калорії шоколадного чізкейка, і, схоже, збереження енергії було порушено, тому що ці калорії не можуть бути належним чином враховані будь-якою взаємодією з B, якого давно немає.

Якщо сподіватися зберегти закон збереження енергії, то єдино можливий висновок - електричне поле саме по собі забирає енергію ватрушки. Насправді цей приклад являє собою непрактичний метод передачі радіохвиль. Аліса працює на заряді А, і ця енергія йде в радіохвилі. Навіть якби Б ніколи не існувало, радіохвилі все одно несли б енергію, і Алісі все одно довелося б зробити роботу, щоб їх створити.

Питання для обговорення

◊ Емі і Білл літають на космічних кораблі в протилежних напрямках з такими високими швидкостями, що легко помітний релятивістський вплив на швидкість потоку часу. Рух відносний, тому Емі вважає себе в спокої, а Білл - в русі. Вона каже, що час тече нормально для неї, але Білл повільний. Але Білл може сказати точно те ж саме. Як вони обидва можуть думати, що інший повільний? Чи можуть вони врегулювати розбіжності, потрапивши на радіо і побачивши, чий голос нормальний, а чиї звуки сповільнилися, а Дарт-Вейдери?

◊ На малюнку зображений відомий експеримент думки, розроблений Ейнштейном. Поїзд рухається з постійною швидкістю вправо, коли болти блискавки вдаряються об землю біля її передньої і задньої частини. Аліса, стоячи на бруді в середній точці спалахів, зауважує, що світло від двох спалахів надходить одночасно, тому вона каже, що два удари, мабуть, відбулися одночасно. Боб, тим часом, сидить на борту поїзда, в його середині. Він проходить повз Алісу в той момент, коли Аліса пізніше з'ясовує, що спалахи сталися. Пізніше він отримує спалах 2, а потім спалах 1. Він робить висновок, що оскільки обидві спалахи пройшли половину довжини поїзда, спалах 2, мабуть, відбувся першим. Як це можна змиритися з переконанням Аліси в те, що спалахи були одночасними? Поясніть за допомогою графіка.

◊ Вирішіть наступний парадокс, намалювавши просторово-часову діаграму (тобто графік\(x\) versus \(t\)). Andy and Beth are in motion relative to one another at a significant fraction of \(c\). As they pass by each other, they exchange greetings, and Beth tells Andy that she is going to blow up a stick of dynamite one hour later. One hour later by Andy's clock, she still hasn't exploded the dynamite, and he says to himself, “She hasn't exploded it because of time dilation. It's only been 40 minutes for her.” He now accelerates suddenly so that he's moving at the same velocity as Beth. The time dilation no longer exists. If he looks again, does he suddenly see the flash from the explosion? How can this be? Would he see her go through 20 minutes of her life in fast-motion?

◊ Використовуйте графік, щоб вирішити наступний парадокс відносності. Відносність говорить про те, що в одній системі відліку подія A могла статися до події B, але в чужому кадрі B прийде до А. Очевидно, що двоє людей могли зустрітися на A і поговорити, коли вони круїздили один за одним. Чи не повинні вони домовитися про те, чи вже відбувся Б?

◊ Вудилище на фігурі ідеально жорстке. При заході А молоток б'є одним кінцем стрижня. На події B інший кінець рухається. Оскільки стрижень ідеально жорсткий, він не може стискати, тому A і B є одночасними. У кадрі 2, B відбувається до А. Чи рух на правому кінці змусив людину зліва вирішити взяти молоток і використовувати його?

7.2.5 Світловий конус

y/Світловий конус.

З огляду на подію P, тепер ми можемо класифікувати всі причинно-наслідкові зв'язки, в яких P може брати участь. У ньютонівській фізиці ці відносини поділялися на два класи: P потенційно може спричинити будь-яку подію, яка лежить в її майбутньому, і могла бути викликана будь-якою подією в минулому. У відносності у нас є тристороння відмінність, а не двостороння. Існує третій клас подій, які знаходяться занадто далеко від P у просторі, і занадто близькі в часі, щоб дозволити будь-які причинно-наслідкові зв'язки, оскільки максимальна швидкість причинно-наслідкового зв'язку є\(c\). Оскільки ми працюємо в одиницях\(c=1\), в яких, межа цієї множини формується лініями з нахилом\(\pm1\) на\((t,x)\) ділянці. Це називається світловим конусом, з причин, які стають більш візуально очевидними, коли ми розглядаємо більше одного просторового виміру, фігуру аа.

aa/ Приклад 9.

Кажуть, що події, що лежать всередині світлих конусів один одного, мають часові стосунки. Події поза світловими конусами один одного є космічними по відношенню один до одного, і в разі, коли вони лежать на поверхнях світлових конусів один одного, термін є світлоподібним. \ myoptionalпідрозділ [2] {Просторово-часовий інтервал}

Світловий конус - об'єкт, що має центральне значення як в особливій, так і в загальній теорії відносності. Він пов'язує геометрію простору-часу з можливими причинно-наслідковими зв'язками між подіями. Це принципово, як працює відносність: це геометрична теорія причинності.

Ці ідеї, природно, змушують нас запитати, які плідні аналогії ми можемо сформувати між химерною геометрією простору-часу і більш звичною геометрією евклідової площини. Світловий конус розрізає простор. час на різні області відповідно до певних вимірювань взаємозв'язків між точками (подіями). Аналогічно, коло в евклідовій геометрії розрізає площину на дві частини, внутрішню та зовнішню, відповідно до вимірювання відстані від центру кола. Коло залишається однаковим, коли ми обертаємо площину. Світлий конус залишається незмінним, коли ми змінюємо рамки відліку. Давайте вибудовуємо аналогію більш явно.

Вимірювання в евклідовій геометрії

Ми говоримо, що два відрізки лінії є конгруентними\(\text{AB}\cong \text{CD}\), якщо відстань між точками A і B таке ж, як відстань між C і D, як вимірюється жорсткою лінійкою.

Вимірювання в просторі-часі

Визначаємо\(\text{AB}\cong \text{CD}\), якщо:

1. AB і CD обидва космічні, і дві відстані рівні, як вимірюється жорсткою лінійкою, в кадрі, де дві події торкаються лінійки одночасно.
2. AB і CD одночасно схожі на час, і два часові інтервали рівні, виміряні годинниками, що рухаються інерційно.
3. AB і CD обидва світлоподібні.

Три частини релятивістської версії вимагають певного обґрунтування.

Випадок 1 повинен бути таким, яким він є, тому що простір є частиною простору-часу. У спеціальній теорії відносності цей простір є евклідовим, тому визначення конгруентності має узгоджуватися з евклідовим визначенням, у випадку, коли можна застосувати евклідове визначення. Просторовий зв'язок між точками є необхідним і достатнім, щоб зробити це можливим. Якщо точки A і B є просторовими по відношенню один до одного, то існує система відліку, в якій вони є одночасними, тому ми можемо використовувати лінійку, яка знаходиться в стані спокою в цьому кадрі, щоб виміряти їх відстань. Якщо вони світлоподібні або часові, то такої системи відліку не існує. Наприклад, немає жодної системи відліку, в якій відновлення Карла VII на престол відбувається одночасно зі стратою Жанни д'Арк, тому ми не можемо домовитися про те, щоб обидві ці події торкнулися одного і того ж правителя одночасно.

Визначення у випадку 2 є єдиним розумним способом продовжити, якщо ми хочемо поважати симетричну обробку часу та простору в теорії відносності. Часоподібне співвідношення між подіями є необхідним і достатнім для того, щоб годинник міг переходити від одного до іншого. Це має значення, що годинник рухаються інерційно, тому що близнюки в прикладі 1 на стор. 391 не погоджуються з часом годинника між від'їздом і поверненням подорожі близнюка.

Випадок 3 може здатися дивним, оскільки він говорить про те, що будь-які два світлоподібних інтервалу є конгруентними. Але це єдино можливе визначення, адже цей випадок можна отримати як ліміт часуподібного. Припустимо, що АВ - це часовоподібний інтервал, але в рамці відліку планети Земля потрібно було б проїхати практично зі швидкістю світла, щоб досягти В від А. Потрібна швидкість менше\(c\) (тобто менше 1) на якусь крихітну величину\(\epsilon\). У земному кадрі годинник, про який йдеться у визначенні, страждає екстремальним тимчасовим розширенням. Час, що минув на годиннику, дуже мало. Оскільки\(\epsilon\) наближається до нуля, а зв'язок між А і В наближається до світлоподібного, цей час годин наближається до нуля. У цьому сенсі релятивістське поняття «відстань» сильно відрізняється від евклідового. У евклідовій геометрії відстань між двома точками може бути лише нулем, якщо вони є однією точкою.

Розщеплення справ, що беруть участь у релятивістському визначенні, трохи потворно. Відпрацювавши фізичну інтерпретацію, тепер ми можемо закріпити визначення приємніше, звернувшись до декартових координат.

Декартове визначення відстані в евклідовій геометрії

Задано вектор\((\Delta x,\Delta y)\) від точки А до точки Б, квадрат відстані між ними визначається як\(\overline{\text{AB}}^2=\Delta x^2+\Delta y^2\).

Визначення інтервалу в відносності

Задані точки, розділені\(\Delta x\) різницею координат\(\Delta y\)\(\Delta z\),\(\Delta t\),, і, проміжок часу\(\mathcal I\) (скорописна буква «I») між ними визначається як\(\mathcal I = \Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2\).

Це зазначено в натуральних одиницях, тому всі чотири терміни з правого боку мають однакові одиниці; в метричних одиницях з\(c \ne 1\), відповідні фактори\(c\) повинні бути вставлені, щоб зробити одиниці термінів узгоджені. Інтервал\(\mathcal I\) є додатним, якщо AB є часовим (незалежно від того, яка подія настане першою), нульовим, якщо світлоподібним, і негативним, якщо пробіл. Оскільки\(\mathcal I\) може бути негативним, ми не можемо взагалі взяти його квадратний корінь і визначити дійсне число\(\overline{\text{AB}}\), як у випадку Евкліда. Коли інтервал є часовим, ми можемо інтерпретувати\(\sqrt{\mathcal I}\) як час, і коли це простір, як ми можемо\(\sqrt{-\mathcal I}\) прийняти відстань.

Евклідове визначення відстані (тобто теорема Піфагора) корисно, оскільки дає однакову відповідь незалежно від того, як ми обертаємо площину. Хоча це заявлено з точки зору певної системи координат, його результат однозначно визначається, оскільки він однаковий незалежно від того, яку систему координат ми довільно вибираємо. \(\mathcal I\)Аналогічно, корисний, оскільки, як доведено в прикладі 8 нижче, він однаковий незалежно від нашої системи відліку, тобто незалежно від нашого вибору координат.

Приклад\(\PageIndex{7}\): Pioneer 10

\(\triangleright\)Космічний зонд Pioneer 10 був запущений в 1972 році, а в 1973 році став першим кораблем, який пролетів повз планету Юпітер. Вона перетнула орбіту планети Нептун в 1983 році, після чого телеметричні дані отримували аж до 2002 року. Наступна таблиця дає положення космічного корабля щодо Сонця рівно опівночі 1 січня 1983 року та 1 січня 1995 року. Дата 1983 року приймається бути\(t=0\).

т (и)	х	у	z
0	1 784 х 10 ^12 м	3 951 х 10 ^12 м	0,237 х 10 ^12 м
3 7869120000 х 10 ^8 с	2.420 х 10 ^12 м	8,827 х 10 ^12 м	0,488 х 10 ^12 м

Порівняйте час, що минув на космічному кораблі, з часом в рамках відліку, прив'язаного до сонця.

\(\triangleright\)Ми можемо перетворити ці дані в природні одиниці, причому одиниця відстані є другою (тобто світловою секундою, відстань світла проходить за одну секунду), а одиниця часу - секунди. Конвертуючи і здійснюючи це віднімання, ми маємо:

Δ т (и)	Δ х	Δ у	Δ z
3 7869120000 х 10 ^8 с	0,212 х 10 ^4 с	1,626 х 10 ^4 с	0,084 х 10 ^4 с

Порівнюючи показники часових і просторових чисел, ми можемо побачити, що космічний апарат рухався зі швидкістю на порядку швидкості світла, тому релятивістські ефекти повинні бути невеликими, але не зовсім незначними.\(10^{-4}\)

Оскільки інтервал схожий на час, ми можемо взяти його квадратний корінь і інтерпретувати його як час, що минув на космічному кораблі. Результат є\(\sqrt{\mathcal I}=3.786911996\times 10^8\ \text{s}\). Це на 0,4 с менше часу, що минув у системі відліку сонця.

z/Світло-прямокутники, приклад 8.
1. Прямокутник сірого світла представляє набір усіх подій, таких як P, які можна було відвідати після A та перед B
2. Прямокутник стає квадратом у кадрі, в якому A і B зустрічаються в одному місці в просторі.
3. Площа пунктирного квадрата дорівнює\(\tau^2\), тому площа сірого квадрата дорівнює\(\tau^2/2\).

Приклад\(\PageIndex{8}\): Invariance of the interval

У цьому прикладі ми доведемо, що інтервал однаковий незалежно від того, в якій системі відліку ми обчислюємо його. Це називається «інваріантність Лоренца». Доказ обмежується часомподібним випадком. Задані події A і B побудувати прямокутник світла, як визначено на малюнку ab /1. На с. 389 доведено, що перетворення Лоренца не змінює площу форми в\(t\) площині\(x\) -. Тому площа цього прямокутника незмінна, якщо ми перейдемо до системи відліку ab /2, в якій A і B відбулися в одному місці і були розділені часовим інтервалом\(\tau\). Ця область дорівнює половині інтервалу\(\mathcal I\) між A і B. Але простий розрахунок показує, що прямокутник в ab /1 також має площу, рівну половині інтервалу, розрахованого в цьому кадрі. Оскільки площа в будь-якому кадрі дорівнює половині інтервалу, а площа однакова у всіх кадрах, інтервал дорівнює і у всіх кадрах.

ab/Приклад 8.

Приклад\(\PageIndex{9}\): A numerical example of invariance

ac/Приклад 9.

На малюнку ac показані дві системи відліку в русі відносно один одного в\(v=3/5\). (Для цієї швидкості розтягування і розтирання основних діагоналей обидва рази 2.) Події позначені за координатами, які в кадрі, представленому квадратом,

\[\begin{align*} (t,x) & = (0,0) \text{and} \\ (t,x) &= (13,11) . \end{align*}\]

Інтервал між цими подіями становить\(13^2-11^2=48\). У кадрі, представленому паралелограмом, за координатами лежать ті ж дві події.

\[\begin{align*} (t',x') & = (0,0) \text{and} \\ (t',x') &= (8,4) . \end{align*}\]

Розраховуючи інтервал за допомогою цих значень
\(8^2-4^2=48\), виходить результат, який виходить таким же, як і в іншому кадрі.

Чотири вектори і внутрішній твір

Приклад 7 робить природним, що ми визначаємо тип вектора з чотирма компонентами, перший з яких стосується часу, а інші - просторовими. Вони відомі як чотири-вектори. Зрозуміло, як ми повинні визначити еквівалент точкового добутку в теорії відносності:

\[\begin{equation*} \mathbf{A}\cdot\mathbf{B} = A_t B_t - A_xB_x - A_yB_y - A_zB_z \end{equation*}\]

Термін «точковий добуток» має конотації позначення лише трьох векторів, тому операція прийняття скалярного добутку двох чотиривекторів зазвичай називають замість «внутрішнього добутку». Просторово-часовий інтервал потім можна розглядати як внутрішній добуток чотири-вектора з самим собою. Ми дбаємо про релятивістський внутрішній продукт з тієї ж причини, що ми дбаємо про його евклідову версію; обидва є скалярами, тому вони мають фіксоване значення незалежно від того, яку систему координат ми обираємо.

Приклад 10: Парадокс близнюків

Аліса і Бетті - однакові близнюки. Бетті відправляється в космічне плавання на релятивістських швидкостях, подорожуючи подалі від землі, а потім обертаючись і повертаючись назад. Тим часом Аліса залишається на землі. Коли Бетті повертається, вона молодша за Алісу через релятивістське розширення часу (приклад 1, стор. 391). Але чи не справедливо сказати, що космічний корабель Бетті стоїть на місці, а земля рухається? У цьому описі, чи не стане Аліса молодшою, а Бетті старшою? Це іменується як «парадокс близнюків». Це насправді не може бути парадоксом, оскільки це саме те, що спостерігалося в експерименті Хафела-Кітінга (стор. 381). Трек Бетті в\(x\) -\(t\) площині (її «світова лінія» на релятивістському жаргоні) складається з векторів\(\mathbf{b}\) і\(\mathbf{c}\) нанизаних впритул (малюнок оголошення). Ми могли б прийняти систему відліку, в якій Бетті перебувала в стані спокою під час\(\mathbf{b}\) (тобто\(b_x=0\)), але немає кадру, в якому\(\mathbf{b}\) і\(\mathbf{c}\) паралельні, тому немає кадру, в якому Бетті перебувала в спокої під час обох\(\mathbf{b}\) і\(\mathbf{c}\). Це вирішує парадокс. Ми вже встановили іншими методами, що Бетті старіє менше, ніж Аліса, але давайте подивимося, як це відбувається на простому числовому прикладі. Опускаючи одиниці і складаючи прості числа, припустимо, що вектори в малюнку оголошення є \[\begin{align*} \mathbf{a} &= (6,1) \\ \mathbf{b} &= (3,2) \\ \mathbf{c} &= (3,-1) , \end{align*}\] де компоненти наведені в порядку\((t,x)\). Час, який переживає Аліса, тоді \[\begin{equation*} |\mathbf{a}| = \sqrt{6^2-1^2} =5.9 , \end{equation*}\] що більше, ніж минулий час Бетті \[\begin{equation*} |\mathbf{b}|+|\mathbf{c}| = \sqrt{3^2-2^2}+\sqrt{3^2-(-1)^2} = 5.1 . \end{equation*}\]

Приклад 11: Одночасність використання внутрішніх виробів

ac/Приклад 11. Припустимо, що спостерігач O рухається інерційно вздовж вектора\(\mathbf{o}\), і нехай вектор, що розділяє дві події P і Q бути\(\mathbf{s}\). O судити ці події, щоб бути одночасними, якщо\(\mathbf{o}\cdot\mathbf{s}=0\). Щоб зрозуміти, чому це правда, припустимо, ми вибираємо систему координат, визначену О. У цій системі координат O вважає себе в спокої, тому вона каже, що її вектор має лише часовий компонент,\(\mathbf{o}=(\Delta t,0,0,0)\). Якщо вона вважає P і Q одночасними, то вектор від P до Q має вигляд\((0,\Delta x,\Delta y,\Delta z)\). Внутрішній твір тоді дорівнює нулю, так як кожен з чотирьох членів зникає. Оскільки внутрішній твір не залежить від вибору системи координат, не має значення, що ми вибрали одну, прив'язану до самої O. Будь-який інший спостерігач\(\text{O}'\) може подивитися на рух О, зауважити це\(\mathbf{o}\cdot\mathbf{s}=0\), і зробити висновок, що O повинен вважати P і Q одночасними, навіть якщо\(\text{O}'\) говорить, що вони не були.

Доплерівські зрушення світла і додавання швидкостей

Коли доплерівські зрушення трапляються з брижами на ставку або звуковими хвилями від літака, вони можуть залежати від відносного руху трьох різних об'єктів: джерела, приймача та середовища. Але легкі хвилі не мають середовища. Тому доплерівські зрушення світла можуть залежати тільки від відносного руху джерела і спостерігача.

оголошення/Візерунок хвиль, зроблений точковим джерелом, що рухається вправо через воду. Зверніть увагу на коротшу довжину хвилі хвиль, що випромінюються вперед, і довшу довжину хвилі зворотних хвиль.

Одним з простих випадків є той, при якому відносний рух джерела і приймача перпендикулярно лінії, що з'єднує їх. Тобто рух поперечне. Нерелятивістські доплерівські зрушення відбуваються через те, що відстань між джерелом і приймачем змінюється, тому в нерелятивістській фізиці ми взагалі не очікуємо жодного доплерівського зсуву, коли рух поперечний, і це те, що насправді спостерігається з високою точністю. Наприклад, на фотографії зображені укорочені і подовжені довжини хвиль праворуч і ліворуч, вздовж лінії руху джерела, але спостерігач вище або нижче джерела вимірює тільки нормальну, незміщену довжину хвилі і частоту. Але релятивістично ми маємо ефект розширення часу, тому для світлових хвиль, випромінюваних поперечно, існує доплерівський\(1/\gamma\) зсув частоти (або\(\gamma\) в довжині хвилі).

Інший простий випадок - той, при якому відносний рух джерела і приймача є поздовжнім, тобто вони або наближаються, або відступають один від одного. Наприклад, далекі галактики відступають від нашої галактики через розширення Всесвіту, і це розширення спочатку було виявлено через те, що спостерігалися доплерівські зрушення в бік червоного (низькочастотного) кінця спектра.

Нерелятивістично, ми очікуємо, що світло від такої галактики буде доплеровскім зміщеним за частотою вниз на певний коефіцієнт, що залежатиме від відносних швидкостей трьох різних об'єктів: джерела, середовища хвилі та приймача. Відносно речі стають простішими, оскільки світло не є вібрацією фізичного середовища, тому доплерівський зсув може залежати лише від однієї швидкості\(v\), яка є швидкістю, з якою збільшується поділ між джерелом та приймачем.

ae/ Графічне зображення перетворення Лоренца для швидкості\((3/5)c\). Довга діагональ розтягується в два рази, коротка - половина колишньої довжини, а площа така ж, як і раніше.

af/У випадку O, джерело і приймач знаходяться один на одного, так як джерело випромінює гребінь хвилі, він приймається без затримки часу. При P джерело випромінює ще один гребінь хвилі, а на Q приймач його отримує.

Квадрат на малюнку af - це «графічний папір», який використовує той, хто вважає джерело в стані спокою, тоді як паралелограм відіграє аналогічну роль для приймача. Малюнок малюється для випадку, коли\(v=3/5\) (в одиницях де\(c=1\)), і в цьому випадку коефіцієнт розтягування довгої діагоналі дорівнює 2. Щоб площа залишалася однаковою, коротку діагональ потрібно розтиснути до половини її початкового розміру. Але тепер це питання простої геометрії, щоб показати, що OP дорівнює половині ширини квадрата, і це говорить нам, що доплерівський зсув є коефіцієнтом 1/2 частоти. Тобто коефіцієнт сквиша короткої діагоналі трактується як доплерівський зсув. Щоб отримати це як загальне рівняння для швидкостей, відмінних від 3/5, можна показати шляхом прямої боротьби з результатом частини c задачі 7 на стор. 439, що доплерівський зсув дорівнює

\[\begin{equation*} D(v) = \sqrt{\frac{1-v}{1+v}} . \end{equation*}\]

\(v>0\)Ось випадок, коли джерело і приймач стають все далі один від одного, випадок,\(v\lt0\) коли вони наближаються. (Це протилежне конвенції про знак, що використовується в підрозділі 6.1.5. Тут зручно змінювати конвенції, щоб ми могли використовувати позитивні значення\(v\) у випадку космологічних червоних зрушень, які є найважливішим додатком.)

Припустимо, що Аліса залишається вдома на землі, поки її близнюк Бетті злітає на своєму ракетному кораблі на 3/5 швидкості світла. Коли я вперше навчився відносності, найбільше мені заподіяло біль, було розуміння того, як кожен спостерігач міг сказати, що інший - той, чий час був повільним. Мені здавалося, що якби я міг прийняти таблетку, яка прискорить мій розум і моє тіло, то, природно, я б бачив усіх інших як повільних. Чи не повинно те ж саме стосуватися відносності? Але припустимо, що Аліса і Бетті потрапляють на радіо і намагаються вирішити, хто швидкий, а хто повільний. Голос кожного близнюка звучить уповільнено doooowwwn до іншого. Якщо Аліса плескає в долоні двічі, з часовим інтервалом в одну секунду за годинником, Бетті чує, як плескають по радіо дві секунди один від одного, але ситуація точно симетрична, і Аліса чує те ж саме, якщо Бетті плескає. Кожен близнюк аналізує ситуацію, використовуючи діаграму, ідентичну ах, і приписує спостереження своєї сестри складному поєднанню спотворення часу, часу, необхідного радіосигналами для поширення, і руху її близнюка щодо неї.

самостійна перевірка:

Переверніть книгу догори дном і переосмислите фігуру ах.

(відповідь у зворотному боці PDF-версії книги)

Приклад 12: Властивість симетрії ефекту Доплера
Припустимо, що А і В знаходяться в спокої відносно один одного, але С рухається по лінії між А і В. А передає сигнал в С, який потім ретранслює його в Б. Сигнал накопичує два доплерівських зрушення, і результат - їх добуток\(D(v)D(-v)\). Але цей твір повинен дорівнювати 1, тому ми повинні мати\(D(-v)D(v)=1\), що можна перевірити безпосередньо з рівняння.

Приклад 13: Експеримент Айвса-Стілвелла

Результат прикладу 12 став основою одного з найбільш ранніх лабораторних тестів спеціальної відносності, проведеного Айвсом і Стілвеллом в 1938 році. Вони спостерігали світло, що випромінюється збудженим пучком\(\text{H}_2^+\) і\(\text{H}_3^+\) іонами зі швидкістю в кілька десятих відсотків\(c\). Вимірюючи світло як попереду, так і ззаду променів, вони виявили, що добуток доплерівських зрушень\(D(v)D(-v)\) дорівнює 1, як передбачено відносністю. Якби відносність була помилковою, то можна було б очікувати, що продукт буде відрізнятися від 1 на суму, яка була б виявлена в їх експерименті. У 2003 році Saathoff et al. провели надзвичайно точну версію методики Івс-Стілвелла з\(\text{Li}^+\) іонами, що рухаються на 6,4%\(c\). Частоти, що спостерігаються, в одиницях МГц, становили: ф о = 546466918,8±0,4 (незміщена частота) f o D (-v) = 582490203,44±0,09 (Зсунута частота, вперед) f о Д (v) = 512671442.9±0,5 (Зсунута частота, назад) \(\sqrt{f_\text{o}D(-v)\cdot f_\text{o} D(v)}\) = 546466918,6±0,3 Результати показують неймовірно точну згоду між\(f_\text{o}\) і\(\sqrt{f_\text{o}D(-v)\cdot f_\text{o} D(v)}\), як очікувалося, релятивістично, оскільки\(D(v)D(-v)\) передбачається дорівнює 1. Угода поширюється на 9 значущих цифр, тоді як якщо відносність була помилковою, мала бути відносна розбіжність про\(v^2=.004\), тобто невідповідність третьої значущої цифри. Вражаюча згода з теорією зробила цей експеримент громовідводом для антивідносних поглядів.

На стор. 394 ми побачили, що релятивістські швидкості не повинні бути точно адитивними, а задача 1 на стор. 438 перевіряє це в особливому випадку, коли A рухається відносно B at\(0.6c\) і B відносно C at\(0.6c\) — результату не буде\(1.2c\). Релятивістський доплерівський зсув забезпечує простий спосіб отримання загального рівняння для релятивістської комбінації швидкостей; задача 17 на с. 442 направляє вас через кроки цієї деривації, а результат наведено на стор. 936.

Дописувачі та атрибуція

• Template:ContribCrowell