10.3: Принцип Гамільтона

Тепер дозвольте мені показати, що рівняння руху Лагранжа, які були виведені в сек. \(2.1\)з законів Ньютона, також може бути отриманий з так званого принципу Гамільтона,\({ }^{16}\) а саме умова мінімуму (а точніше екстремума) наступного інтеграла, званого дією:\[S \equiv \int_{t_{\text {ini }}}^{t_{\text {fin }}} L d t,\] де\(t_{\text {ini }}\) і\(t_{\text {fin }}\) знаходяться, відповідно, початковий і кінцевий моменти час, при якому всі узагальнені координати і швидкості вважаються фіксованими (не змінюються) - див. Рис.\(2 .\)

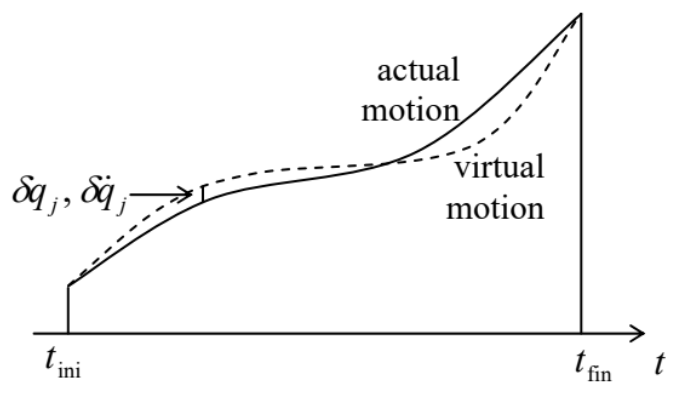Малюнок 10.2. Виведення принципу Гамільтона.

Доказ цього твердження (у царині класичної механіки) досить простий. Враховуючи, подібно до п. 2.1, можливу віртуальну варіацію руху, описану нескінченно малими відхиленнями\(\left\{\delta q_{j}(t), \delta \dot{q}_{j}(t)\right\}\) від реального руху, необхідною умовою для\(S\) того, щоб бути мінімальним,\(\delta L\) є\[\delta S \equiv \int_{t_{\text {ini }}}^{t_{\text {fin }}} \delta L d t=0,\] де\(\delta S\) і є варіації дії та Функція Лагранжа, відповідна множині\(\left\{\delta q_{j}(t), \delta \ddot{q}_{j}(t)\right\}\). Як вже обговорювалося в п. 2.1, ми можемо використовувати операцію варіації так само, як звичайну диференціацію (але у фіксований час, див. Рисунок 2), міняючи ці дві операції, якщо це необхідно, див. Рисунок\(2.3\) та його обговорення. Таким чином, ми можемо написати\[\delta L=\sum_{j}\left(\frac{\partial L}{\partial q_{j}} \delta q_{j}+\frac{\partial L}{\partial \dot{q}_{j}} \delta \ddot{q}_{j}\right)=\sum_{j} \frac{\partial L}{\partial q_{j}} \delta q_{j}+\sum_{j} \frac{\partial L}{\partial \dot{q}_{j}} \frac{d}{d t} \delta q_{j} .\] Після підключення останнього виразу до Eq. (48), ми можемо інтегрувати другий член частинами:\[\begin{aligned} \delta S &=\int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \sum_{j} \frac{\partial L}{\partial q_{j}} \delta q_{j} d t+\sum_{j} \int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \frac{\partial L}{\partial \dot{q}_{j}} \frac{d}{d t} \delta q_{j} d t \\ &=\int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \sum_{j} \frac{\partial L}{\partial q_{j}} \delta q_{j} d t+\sum_{j}\left[\frac{\partial L}{\partial \dot{q}_{j}} \delta q_{j}\right]_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}}-\sum_{j} \int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \delta q_{j} d\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)=0 \end{aligned}\] Оскільки узагальнені координати у початковій та кінцевій точках вважаються фіксованими (не впливають на зміну), все\(\delta q_{j}\left(t_{\mathrm{ini}}\right)\) і \(\delta q_{j}\left(t_{\mathrm{fin}}\right)\)зникають, так що другий член в останній формі Eq. (50) також зникає. Тепер множивши і діливши останній член цього виразу на\(d t\), ми, нарешті, отримаємо\[\delta S=\int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \sum_{j} \frac{\partial L}{\partial q_{j}} \delta q_{j} d t-\sum_{j} \int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \delta q_{j} \frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right) d t=-\int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \sum_{j}\left[\frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial q_{j}}\right] \delta q_{j} d t=0\] Це відношення повинно триматися для довільного набору функцій\(\delta q_{j}(t)\), і для будь-якого часового інтервалу, і це можливо тільки в тому випадку, якщо вирази в квадратних дужках дорівнюють нулю для всіх \(j\), даючи нам множину рівнянь Лагранжа (2.19). Отже, принцип Гамільтона дійсно дає рівняння руху Лагранжа.

Цікаво побачити, як працює принцип Гамільтона для конкретних випадків. Як дуже простий приклад, розглянемо звичайний 1D лінійний генератор, з функцією Лагранжа, яка використовується так багато разів раніше в цьому курсі:\[L=\frac{m}{2} \dot{q}^{2}-\frac{m \omega_{0}^{2}}{2} q^{2} .\] Як ми знаємо дуже добре, рівняння руху Лагранжа для цього точно\(L\) задовольняються будь-якою синусоїдальною функцією з частотою \(\omega_{0}\), Зокрема симетричною функцією часу\[q_{\mathrm{e}}(t)=A \cos \omega_{0} t, \quad \text { so that } \dot{q}_{\mathrm{e}}(t)=-A \omega_{0} \sin \omega_{0} t .\] На обмеженому часовому інтервалі, скажімо\(0 \leq \omega_{0} t \leq+\pi / 2\), ця функція досить плавна і може бути добре наближена іншими простими, розумно підібраними функціями часу, наприклад за\[q_{\mathrm{a}}(t)=A\left(1-\lambda t^{2}\right), \quad \text { so that } \dot{q}_{\mathrm{a}}(t)=-2 A \lambda t,\] умови, що параметр \(\lambda\)підбирається також розумним чином. Візьмемо\(\lambda=\left(\pi / 2 \omega_{0}\right)^{2}\), щоб наближена функція\(q_{\mathrm{a}}(t)\) збігалася з точною функцією\(q_{\mathrm{e}}(t)\) на обох кінцях нашого часового інтервалу (рис. 3):\[q_{\mathrm{a}}\left(t_{\mathrm{ini}}\right)=q_{\mathrm{e}}\left(t_{\mathrm{ini}}\right)=A, \quad q_{\mathrm{a}}\left(t_{\mathrm{fin}}\right)=q_{\mathrm{e}}\left(t_{\mathrm{fin}}\right)=0, \quad \text { where } t_{\mathrm{ini}} \equiv 0, \quad t_{\mathrm{fin}} \equiv \frac{\pi}{2 \omega_{0}},\] і перевіримо, який з них принцип Гамільтона «віддає перевагу», тобто яка функція дає найменшу дію.

Малюнок 10.3. Ділянки функцій,\(q(t)\) заданих Eqs. (53) і (54).

Елементарний розрахунок дії (47), що відповідає цим двом функціям, виходить\[S_{\mathrm{e}}=\left(\frac{\pi}{8}-\frac{\pi}{8}\right) m \omega_{0} A^{2}=0, \quad S_{\mathrm{a}}=\left(\frac{4}{3 \pi}-\frac{2 \pi}{15}\right) m \omega_{0} A^{2} \approx(0.4244-0.4189) m \omega_{0} A^{2}>0,\] з першими членами у всіх дужках, що надходять від тимчасових інтегралів кінетичної енергії, а другі члени, з тих потенційної енергії.

Цей результат показує, по-перше, що точна функція часу, за яку ці два внески точно скасовуються,\({ }^{17}\) дійсно «краща» для мінімізації дії. По-друге, для наближеної функції два внески в дію досить близькі до точних, а значить, майже скасовують один одного, сигналізуючи про те, що це наближення дуже розумне. Очевидно, що в деяких випадках, коли точного аналітичного рішення рівнянь руху не вдається знайти, мінімізація\(S\) шляхом коригування одного або декількох вільних параметрів, включених у вгадану «пробну» функцію, може бути використана для пошуку розумного наближення для фактичного закону руху. також дуже корисно зробити поняття дії\(S\), визначене Eq. (47), більш прозорим шляхом обчислення його для простого випадку однієї частинки, що рухається в потенційному полі, яке зберігає свою енергію\(E=T+U\). У цьому випадку функція Лагранжа\(L=T-U\) може бути представлена як\[L=T-U=2 T-(T+U)=2 T-E=m v^{2}-E,\] з незалежною від часу\(E\), так що\[S=\int L d t=\int m v^{2} d t-E t+\text { const. }\] Представляючи вираз під залишився інтегралом як\(m \mathbf{v} \cdot \mathbf{v} d t=\mathbf{p} \cdot(d \mathbf{r} / d t) d t=\mathbf{p} \cdot d \mathbf{r}\), ми нарешті отримаємо,\[S=\int \mathbf{p} \cdot d \mathbf{r}-E t+\text { const }=S_{0}-E t+\text { const },\] де час незалежний інтеграл часто\[S_{0} \equiv \int \mathbf{p} \cdot d \mathbf{r}\] називають скороченим дією.

Цей вираз може бути використаний для встановлення ще одного важливого зв'язку між класичною та квантовою механікою - тепер у своїй картині Шредінгера. Дійсно, у квазікласичному (WKB) наближенні цієї картини\({ }^{19}\) частинка фіксованої енергії описується хвилею\[\Psi(\mathbf{r}, t) \propto \exp \left\{i\left(\int \mathbf{k} \cdot d \mathbf{r}-\omega t+\text { const }\right)\right\},\] де Броля, де\(\mathbf{k}\) хвильовий вектор пропорційний імпульсу частинки, а частота\(\omega\) - її енергії:\[\mathbf{k}=\frac{\mathbf{p}}{\hbar}, \quad \omega=\frac{E}{\hbar} .\] Підключивши ці вирази до Eq. (61) і порівнюючи результат з Eq. (59), ми бачимо, що хвильова функція WKB може бути представлена як\[\Psi \propto \exp \{i S / \hbar\} .\] Отже, принцип Гамільтона (48) означає, що загальна фаза квазікласичної хвильової функції повинна бути мінімальною вздовж реальної траєкторії частинки. Але це саме так званий принцип ейконального мінімуму, добре відомий з оптики (хоча і для будь-яких інших хвиль), де він служить для визначення шляхів променів у межі геометричної оптики - подібно до умови наближення WKB. Таким чином, співвідношення\(S / \hbar\) може розглядатися так само, як ейкональне, тобто повне фазове накопичення, хвиль де Броля. \({ }^{20}\)

Тепер, порівнюючи Eq. (60) з Eq. (39), ми бачимо, що змінна дії\(J\) - це всього лише зміна скороченого дії\(S_{0}\) уздовж одного контуру фазової площини (поділена на\(2 \pi\)). Це означає, зокрема, що в наближенні WKB\(J\) є число хвиль де Броля по класичній траєкторії частинки, тобто ціле значення відповідного квантового числа. Якщо параметри системи змінюються повільно, квантове число має залишатися цілим і, отже,\(J\) не може змінюватися, даючи квантово-механічну інтерпретацію адіабатичної інваріантності. Це дійсно захоплююче: факт класичної механіки може бути «виведений» (або, принаймні, зрозумілий) легше з точки зору квантової механіки. \({ }^{21}\)

---

\({ }^{16}\)Його ще називають «принципом найменшої дії», або «принципом стаціонарної дії». (Ці імена можуть бути більш справедливими в контексті багаторічної історії розвитку принципу, починаючи від його більш простих окремих форм, до яких відносяться імена П. де Ферма, П. Мопертюа, Л.Ейлера, і Ж.-Л. Лагранж.)

\({ }^{17}\)Таке скасування, тобто рівність\(S=0\), звичайно, не є загальною вимогою; воно специфічне лише для цього конкретного прикладу.

\({ }^{18}\)Це по суті класичний аналог варіаційного методу квантової механіки - див., наприклад, QM Sec. \(2.9 .\)

\({ }^{19}\)Див., наприклад, QM Розділ 3.1.

\({ }^{20}\)Дійсно, еквалайзер (63) був відправною точкою для розробки Р.Фейнмана його інтегральної формулювання квантової механіки - див., наприклад, QM Sec. 5.3.

\({ }^{21}\)Нагадаємо, ми зіткнулися з подібним приємним сюрпризом під час обговорення невиродженого параметричного збудження в с. \(6.7\).

\({ }^{22}\)Див., наприклад, глави 6-9 в I. C. Percival і D.Richards, Вступ до динаміки, Cambridge U. прес,\(1983 .\)