9.1: Хаос на картах

Можливість квазівипадкової динаміки детермінованих систем з декількома ступенями свободи (нині називається детермінованим хаосом - або просто «хаосом») була помічена ще до\(20^{\text {th }}\) століття,\({ }^{1}\) але отримала широке визнання лише після публікації теоретичної статті 1963 року метеоролог Едвард Лоренц. У цій роботі він розглядав чисельні розв'язки наступної системи трьох нелінійних звичайних диференціальних рівнянь,\[\begin{aligned} \dot{q}_{1} &=a_{1}\left(q_{2}-q_{1}\right) \\ \dot{q}_{2} &=a_{2} q_{1}-q_{2}-q_{1} q_{3}, \\ \dot{q}_{3} &=q_{1} q_{2}-a_{3} q_{3}, \end{aligned}\] як рудиментарну модель теплообміну через горизонтальний шар рідини, що розділяє дві тверді пластини. (Експеримент показує, що якщо нижня пластина тримається гарячішою, ніж верхня, рідина може проявляти турбулентну конвекцію.) Він виявив, що в певному діапазоні констант\(a_{1,2,3}\) рішення Eq. (1) слідує за складними, непередбачуваними, неповторюваними траєкторіями в 3D\(q\) -просторі. Причому функції\(q_{j}(t)\) (де\(j=1,2,3\)) настільки чутливі до початкових умов,\(q_{j}(0)\) що в досить великий час розв'язки\(t\), відповідні дещо іншим початковим умовам, стають абсолютно різними.

Дуже скоро стало зрозуміло, що така поведінка характерно для ще більш простих математичних об'єктів, званих картами, так що я почну своє обговорення хаосу саме з цих об'єктів. 1D карта - це, по суті, правило для знаходження наступного числа\(q_{n+1}\) дискретної послідовності, пронумерованої цілочисельним індексом\(n\), в найпростіших випадках з використанням тільки останнього відомого значення\(q_{n}\). Найвідомішим прикладом є так звана\(\operatorname{logistic}\) карта:\(^{2}\)\[q_{n+1}=f\left(q_{n}\right) \equiv r q_{n}\left(1-q_{n}\right) .\] Основні властивості цієї карти можна зрозуміти за допомогою графічного зображення (сподіваюся, без пояснення), показаного на малюнку 1. \({ }^{3}\)Можна легко помітити, що на\(r<1\) (рис. 1а) послідовність логістичної карти швидко сходиться до тривіальної фіксованої точки\(q^{(0)}=0\), оскільки кожне наступне значення менше попереднього.\(q\) Однак при\(r\) збільшенні вище 1 (як у прикладі, показаному на малюнку 1б), фіксована точка\(q^{(0)}\) стає нестійкою. Дійсно\(q_{n}<<1\), в, карта дає\(q_{n+1} \approx r q_{n}\), так що при\(r>1\), значення\(q_{n}\) ростуть з кожною ітерацією. Замість нестабільної точки\(q^{(0)}=0\), в діапазоні\(1<r<r_{1}\)\(r_{1} \equiv 3\), де карта має стабільну фіксовану точку,\(q^{(1)}\) яку можна знайти, підключивши це значення до обох частин Eq. (2):\[q^{(1)}=f\left(q^{(1)}\right) \equiv r q^{(1)}\left(1-q^{(1)}\right),\] даючи\(q^{(1)}=1-1 / r-\) побачити ліву гілку графіка, показаного на малюнку\(2 .\)

Малюнок 9.1. Графічний аналіз логістичної карти для: (a)\(r<1\) та (b)\(r>1\).

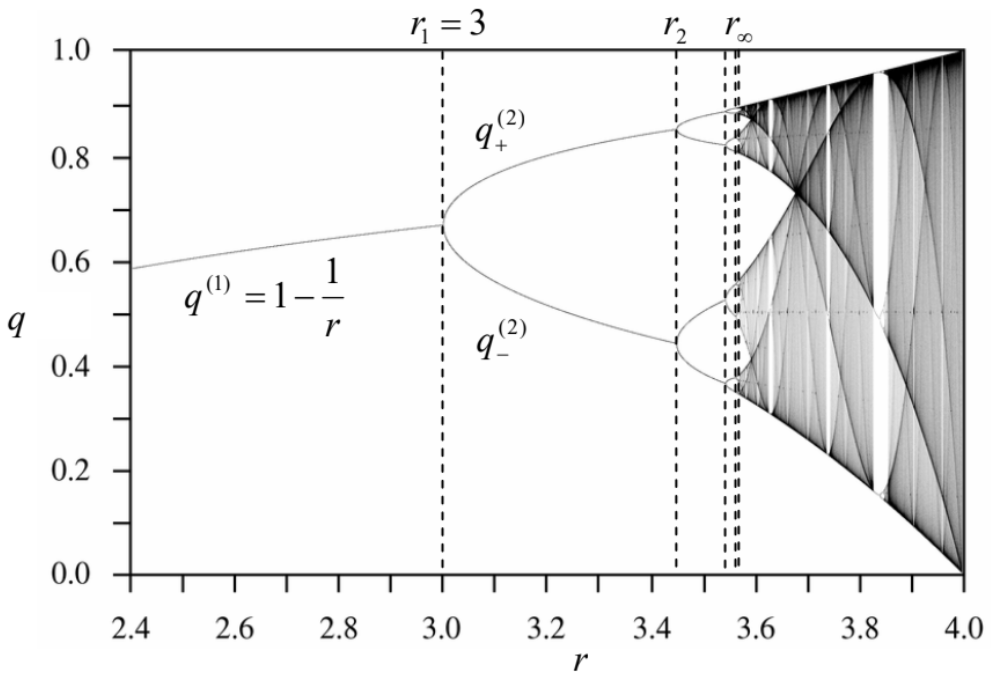Малюнок 9.2. Фіксовані точки та хаотичні регіони логістичної карти. Адаптовано, під CCO 1.0 Всесвітнє присвячення громадського надбання, з оригіналу Джордана Пірса, доступний за адресою http://en.wikipedia.org/wiki/Logistic_map. (Дуже приємна жива симуляція карти також доступна на цьому веб-сайті.)

Однак при\(r>r_{1}=3\), нерухома точка\(q^{(1)}\) також стає нестійкою. Щоб довести\(q^{(1)}\) це, візьмемо
\(q_{n} \equiv q^{(1)}+\widetilde{q}_{n}\), припустимо, що відхилення\(\widetilde{q}_{n}\) від фіксованої точки невелике, і лінеаризувати карту (2)
так\(\widetilde{q}_{n}-\) само, як ми неодноразово робили для диференціальних рівнянь раніше в цьому курсі. Результат\[\widetilde{q}_{n+1}=\left.\frac{d f}{d q}\right|_{q=q^{(1)}} \widetilde{q}_{n}=r\left(1-2 q^{(1)}\right) \widetilde{q}_{n}=(2-r) \widetilde{q}_{n} .\] Довести це, візьмемо\[\widetilde{q}_{n+1}=\left.\frac{d f}{d q}\right|_{q=q^{(1)}} \tilde{q}_{n}=r\left(1-2 q^{(1)}\right) \widetilde{q}_{n}=(2-r) \widetilde{q}_{n} .\] Це показує, що при\(0<2-r<1\), тобто при\(1<r<2\), відхилення\(\widetilde{q}_{n}\) зменшуються монотонно. В\(-1<2-r\)\(<0\), тобто в діапазоні\(2<r<3\), знак відхилень чергується, але їх величина все одно зменшується,\(-\) як і в стабільному фокусі, див. Розділ 5.6. Однак при\(-1<2-r\)\(r>r_{1} \equiv 3\), тобто відхилення ростуть за величиною, при цьому все ж змінюючи свій знак, на кожному кроці. Так як екв. (2) не має інших фіксованих точок, це означає, що при\(n\)\(\rightarrow \infty\), значення\(q_{n}\) не сходяться в одну точку; скоріше, в межах діапазону\(r_{1}<r<r_{2}\) вони наближаються до граничного циклу чергування двох точок,\(q_{+}{ }^{(2)}\) і\(q_{-}{ }^{(2)}\), які задовольняють наступну систему алгебраїчні рівняння:\[q_{+}^{(2)}=f\left(q_{-}^{(2)}\right), \quad q_{-}^{(2)}=f\left(q_{+}^{(2)}\right) .\] Ці точки також побудовані на малюнку 2, як функції параметра\(r\). Те, що сталося в точці,\(r_{1}\)\(=3\) називається періодом-подвоєння біфуркації.

Історія повторюється в тому\(r=r_{2} \equiv 1+\sqrt{6} \approx 3.45\), де система переходить від 2-точкового граничного циклу до 4-точкового циклу, потім в\(r=r_{3} \approx 3.54\), де граничний цикл стає складається з 8 чергуються точок і т.д. найбільш примітно, період подвоєння точок біфуркації\(r_{n}\), при цьому кількість точок в граничному циклі подвоюється від\(2^{n-1}\) точок до\(2^{n}\) точок, ставати все ближче і ближче. Чисельні розрахунки показують\(n \rightarrow \infty\), що в цих точках дотримується наступної асимптотичної поведінки:\[r_{n} \rightarrow r_{\infty}-\frac{C}{\delta^{n}}, \text { where } r_{\infty}=3.5699 \ldots, \quad \delta=4.6692 \ldots\] параметр\(\delta\) називається постійною Фейгенбаума; для інших карт та деяких динамічних систем (див. Наступний розділ) послідовності подвоєння періодів слідують аналогічному закону, але з різними значеннями з\(\delta\).

Більш важливим для нас, однак, є те, що відбувається в\(r>r_{\infty} .\) Численні чисельні експерименти, повторювані з підвищенням точності,\({ }^{4}\) підтвердили, що тут система повністю невпорядкована, без відтворюваного граничного циклу, хоча (як показано на малюнку 2) в\(r \approx r_{\infty}\), всі\(q_{n}\) послідовні значення все ще обмежується кількома вузькими регіонами. \({ }^{5}\)Однак, оскільки параметр збільшується\(r\) далеко за межі\(r_{\infty}\), ці регіони розширюються та зливаються. Це так званий глибокий хаос, без видимого порядку взагалі. \({ }^{6}\)

Найголовніша особливість хаосу (в цій і будь-якій іншій системі) - експоненціальна розбіжність траєкторій. Для 1D карти це означає, що навіть якщо початкові умови\(q_{1}\) в двох реалізаціях карт відрізняються на дуже малу величину\(\Delta q_{1}\), різниця\(\Delta q_{n}\) між відповідними послідовностями\(q_{n}\) зростає, в середньому, експоненціально с\(n\). Такі показники можуть бути використані для характеристики хаосу. Дійсно, очевидне узагальнення Eq. (4) до довільної точки\(q_{n}\) є\[\Delta q_{n+1}=e_{n} \Delta q_{n},\left.\quad e_{n} \equiv \frac{d f}{d q}\right|_{q=q_{n}} .\] Припустимо, що\(\Delta q_{1}\) це настільки мало, що\(N\) перші значення\(q_{n}\) відносно близькі один до одного. Потім за допомогою еквалайзера (7) для цих кроків ми отримуємо\[\Delta q_{N}=\Delta q_{1} \prod_{n=1}^{N} e_{n}, \quad \text { so that } \ln \left|\frac{\Delta q_{N}}{\Delta q_{1}}\right|=\sum_{n=1}^{N} \ln \left|e_{n}\right| \text {. }\] Числові експерименти показують, що в більшості хаотичних режимів при\(N \rightarrow \infty\) такій сумі коливається приблизно середнє значення\(\lambda N\), яке зростає як, при цьому параметр, який\[\lambda \equiv \lim _{\Delta q_{1} \rightarrow 0} \lim _{N \rightarrow \infty} \frac{1}{N} \sum_{n=1}^{N} \ln \left|e_{n}\right|,\] називається\({ }^{7}\) показником Ляпунова, незалежний від початкові умови. Нижня панель на малюнку 3 показана\(\lambda\) як функція параметра\(r\) для логістичної карти (2). (Його верхня панель показує ті ж дані, що і на малюнку 2, і вона відтворена тут тільки заради порівняння.)

Малюнок 9.3. Показник Ляпунова для логістичної карти. Адаптовано, з дозволу, з монографії Шустера та Джаста (наведено нижче). C Вілі-ВЧ Верлаг\(\mathrm{GmbH}\) & Ко. КгаА.

Зауважте, що at\(r<r_{\infty}, \lambda\) є негативним, що вказує на стабільність послідовності, окрім точок,\(r_{1}, r_{2}, \ldots\) де стане позитивним,\(\lambda\) якби зміни граничного циклу (біфуркації) не повернули її назад на негативну територію. Однак at\(r>r_{\infty}, \lambda\) стає позитивним, повертаючись до негативних значень лише в обмежених інтервалах стабільних граничних циклів. Очевидно, що в чисельних експериментах (які домінують у дослідженнях детермінованого хаосу) показник Ляпунова може бути використаний як хороший показник глибини хаосу. \({ }^{8}\)

Незважаючи на всю велику кількість результатів, опублікованих для конкретних карт,\({ }^{9}\) і кілька цікавих загальних спостережень (наприклад, існування послідовностей біфуркації Фейгенбаума), наскільки мені відомо, ніхто ще не може передбачити закономірності, подібні до тих, що показані на малюнку 2 та 3, просто дивлячись на власне правило відображення, тобто без проведення фактичних числових експериментів. На жаль, розуміння детермінованого хаосу в інших системах не набагато краще.

---

\({ }^{1}\)Це може бути простежено принаймні до паперу 1892 року того ж Жюля Анрі Пуанкаре, який вже був благоговінно згаданий у главі 5. Посилаючись на це: «... може статися, що невеликі відмінності в початкових умовах породжують дуже великі в кінцевих явищах. [...] Передбачення стає неможливим».

\({ }_{2}\)Його хаотичні властивості вперше обговорювалися в 1976 році Робертом Мей, хоча сама карта є однією з простих екологічних моделей, які неодноразово обговорювалися набагато раніше, і може бути простежена принаймні до 1838 роботи П'єра Франсуа Верхулста.

\({ }^{3}\)Оскільки максимальне значення функції\(f(q)\), досягнуте при\(q=1 / 2\), дорівнює\(r / 4\), відображення може бути обмежено сегментом\(x=[0,1]\), якщо параметр\(r\) знаходиться в межах від 0 до 4. Оскільки всі цікаві властивості карти, включаючи хаос, можна знайти в цих межах, я буду обговорювати тільки цей діапазон\(r\).

\({ }^{4}\)Читач повинен пам'ятати, що так само, як і звичайні («натурні») експерименти, чисельні експерименти також мають обмежену точність, обумовлену неминучими похибками округлення.

\({ }^{5}\)Геометрія цих областей, по суті, фрактальна, тобто має проміжний проміжок розмірності між 0 (який матиме будь-яка кінцева множина геометричних точок) та 1 (що стосується одномерного континууму). Широке обговорення фрактальної геометрії та їх зв'язку з детермінованим хаосом можна знайти, наприклад, у книзі Б.Мандельброта, Фрактальна геометрія природи, W.H. Freeman,\(1983 .\)

\({ }^{6}\)Це не означає, що розвиток хаосу завжди є монотонною функцією\(r\). Як показує малюнок 2, протягом певних інтервалів цього параметра хаотична поведінка раптово зникає, замінюючись, як правило, на кілька точкових граничних циклів, просто для відновлення на іншій стороні інтервалу. Іноді (але не завжди!) «шлях до хаосу» на кордоні цих інтервалів слідує за тією ж Фейгенбаумом послідовності дворазових біфуркацій.

\({ }^{7}\)Після Олександра Михайловича Ляпунова (1857-1918), прославився своїми дослідженнями стійкості динамічних систем.

\({ }^{8} N\)-розмірні карти, які стосуються\(N\) -мірних векторів, а не скалярів, можуть характеризуватися показниками\(N\) Ляпунова, а не одиницею. Для хаотичної поведінки досить лише одного з них стати позитивним. Для таких систем може бути більш актуальною інша міра хаосу - ентропія Колмогорова. Ця міра, і її зв'язок з показниками Ляпунова обговорюються, наприклад, в С.М. \(2.2\).

\({ }^{9}\)Див., наприклад, глави 2-4 в H. Schuster і W. Just, Детермінований хаос,\(4^{\text {th }}\) ред., Wiley-VCH, 2005, або глави 8-9 в J. Thompson and H. Stewart, Нелінійна динаміка і хаос,\(2^{\text {nd }}\) ред., Wiley, 2002.