Skip to main content
LibreTexts - Ukrayinska

27.3: Тиск у рідині

  1. Last updated
  2. Save as PDF
  • Page ID
    75551

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Коли на поверхню рідини прикладається сила зсуву, рідина зазнає потоку. Коли рідина статична, сила на будь-якій поверхні всередині рідини повинна бути перпендикулярною (нормальною) кожній стороні цієї поверхні. Ця сила обумовлена зіткненнями між молекулами рідини з одного боку поверхні з молекулами з іншого боку. Для статичної рідини ці сили повинні дорівнювати нулю. Розглянемо невелику порцію статичної рідини, показану на малюнку 27.1. Ця частина рідини розділена на дві частини, які ми позначимо 1 і 2, невеликим математичним розділеним поверхневим\(S\) елементом площі\(A_{S}\). Сила\(\overrightarrow{\mathbf{F}}_{1,2}(S)\) на\(S\) поверхні області 2 внаслідок зіткнень між молекулами 1 і 2 перпендикулярна поверхні.

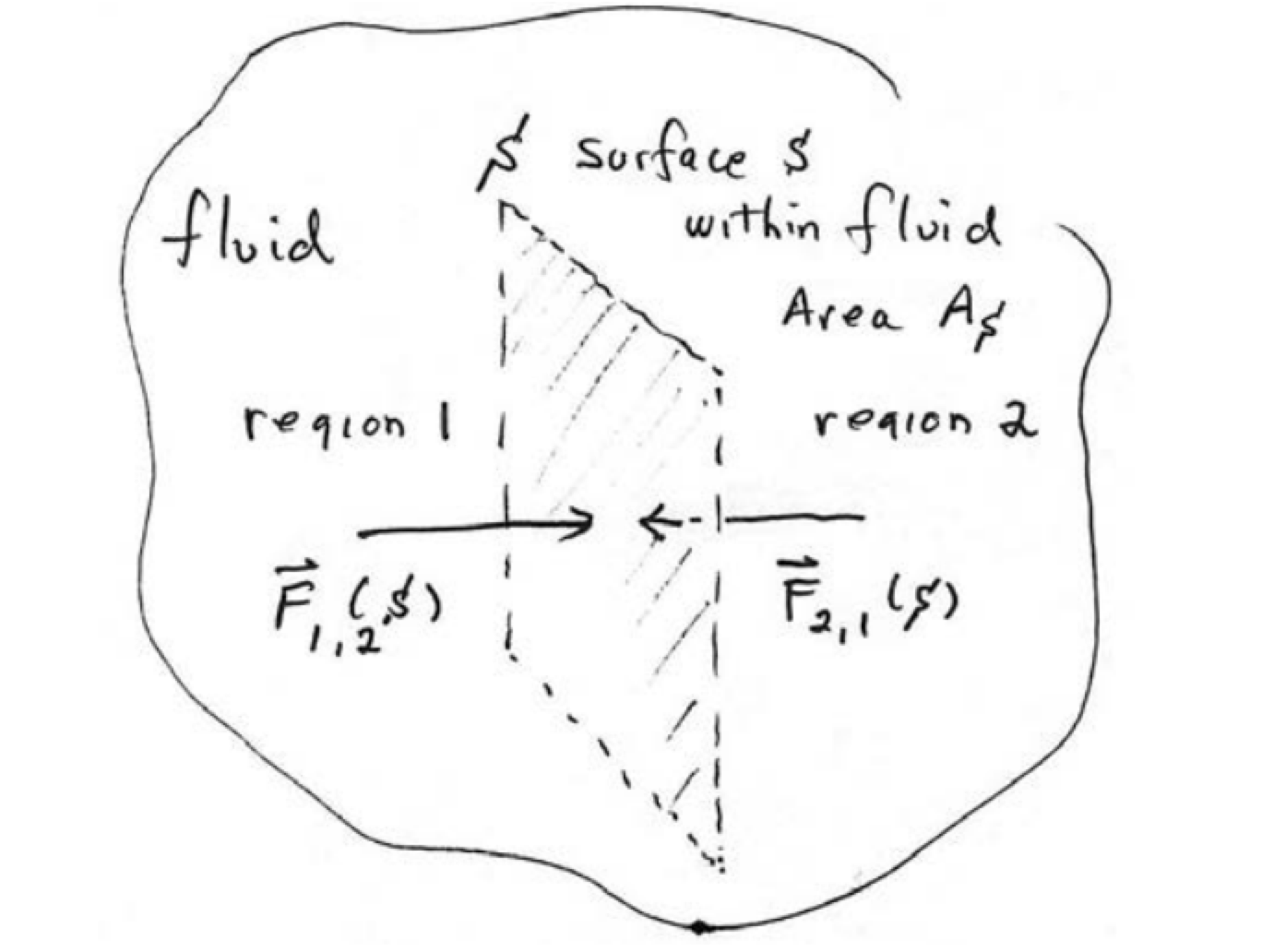
    clipboard_e531eff975b97c9fd2210204802c2192d.png
    Малюнок 27.1: Сили на поверхні всередині рідини

    Сила\(\overrightarrow{\mathbf{F}}_{21}(S)\) на поверхні області 1 внаслідок зіткнень між молекулами 1 і 2 по Третьому закону Ньютона задовольняє\[\overrightarrow{\mathbf{F}}_{1,2}(S)=-\overrightarrow{\mathbf{F}}_{2,1}(S) \nonumber \] Позначити величину цих сил, що утворюють цю пару взаємодії шляхом\[F_{\perp}(S)=\left|\overrightarrow{\mathbf{F}}_{1,2}(S)\right|=\left|\overrightarrow{\mathbf{F}}_{2,1}(S)\right| \nonumber \] Визначення гідростатичного тиску в тих точках всередині рідини, які лежать на поверхня\(S\)\[P \equiv \frac{F_{\perp}(S)}{A_{S}} \nonumber \] по Тиск в точці на поверхні\(S\) є межею\[P=\lim _{A_{S} \rightarrow 0} \frac{F_{\perp}(S)}{A_{S}} \nonumber \] Одиниці СІ для тиску є\(\mathrm{N} \cdot \mathrm{m}^{-2}\) і називається паскалем (Па), де\[1 \mathrm{Pa}=1 \mathrm{N} \cdot \mathrm{m}^{-2}=10^{-5} \mathrm{bar} \nonumber \] Атмосферний тиск в точці - це сила на одиницю площі, що чиниться на малій поверхні, що містить цю точку по вага повітря над цією поверхнею. У більшості випадків атмосферний тиск тісно наближається гідростатичним тиском, викликаним вагою повітря над точкою вимірювання. На даній площі поверхні ділянки низького тиску мають меншу атмосферну масу над своїм розташуванням, тоді як ділянки високого тиску мають більшу атмосферну масу над їх розташуванням. Так само зі збільшенням висоти виникає менше вищерозташованої атмосферної маси, так що атмосферний тиск зменшується зі збільшенням висоти. В середньому стовп повітря на один квадратний сантиметр в поперечному перерізі, вимірюваний від рівня моря до вершини атмосфери, має масу близько 1,03 кг і вагу близько 10,1 Н. (Колонка на один квадратний дюйм в поперечному перерізі мала б вагу близько 14,7 фунтів, або близько 65,4 Н). Стандартна атмосфера [атм] - одиниця тиску така, що\[1 \mathrm{atm}=1.01325 \times 10^{5} \mathrm{Pa}=1.01325 \mathrm{bar} \nonumber \]