13.12: Додаток 13А Робота над системою двох частинок

Покажемо, що робота, виконана внутрішньою силою при зміні системи з двох частинок мас\(m_{1}\) і\(m_{1}\) відповідно від початкового стану А до кінцевого стану В дорівнює

\[W_{\mathrm{c}}=\frac{1}{2} \mu\left(v_{B}^{2}-v_{A}^{2}\right) \nonumber \]

де\(v_{B}^{2}\) - квадрат відносної швидкості в стані B,\(v_{A}^{2}\) - квадрат відносної швидкості в стані А, і\(\mu=m_{1} m_{2} /\left(m_{1}+m_{2}\right)\).

Розглянемо два тіла 1 і 2 і пару сил взаємодії, показану на малюнку 13A.1.

Малюнок 13A.1 Система двох тіл, що взаємодіють

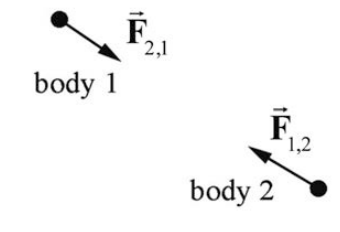
Вибираємо систему координат, показану на малюнку 13А.2.

Рисунок 13A.2 Система координат взаємодії двох тіл

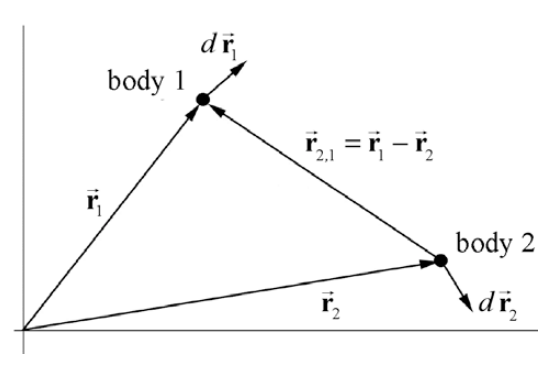
Другий закон Ньютона, застосований до тіла 1, є

\[\overrightarrow{\mathbf{F}}_{2,1}=m_{1} \frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}} \nonumber \]

і застосовується до тіла 2

\[\overrightarrow{\mathbf{F}}_{1,2}=m_{2} \frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}} \nonumber \]

Розділіть кожну сторону рівняння (13.1.2) на\(m_{1}\),

\[\frac{\overrightarrow{\mathbf{F}}_{2,1}}{m_{1}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}} \nonumber \]

і розділити кожну сторону рівняння (13.1.3) на\(m_{2}\),

\[\frac{\overrightarrow{\mathbf{F}}_{1,2}}{m_{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}} \nonumber \]

Відніміть рівняння (13.1.5) з рівняння (13.1.4), що дає

\[\frac{\overrightarrow{\mathbf{F}}_{2,1}}{m_{1}}-\frac{\overrightarrow{\mathbf{F}}_{1,2}}{m_{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}}-\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \nonumber \]

де\(\overrightarrow{\mathbf{r}}_{2,1}=\overrightarrow{\mathbf{r}}_{1}-\overrightarrow{\mathbf{r}}_{2}\). Використовуйте Третій закон Ньютона\(\overrightarrow{\mathbf{F}}_{2,1}=-\overrightarrow{\mathbf{F}}_{1,2}\) на лівій стороні рівняння (13.1.6), щоб отримати

\[\overrightarrow{\mathbf{F}}_{2,1}\left(\frac{1}{m_{1}}+\frac{1}{m_{2}}\right)=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}}-\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \nonumber \]

\(d^{2} \overrightarrow{\mathbf{r}}_{1,2} / d t^{2}\)Величина - відносне прискорення тіла 1 по відношенню до тіла 2.

Визначте

\[\frac{1}{\mu} \equiv \frac{1}{m_{1}}+\frac{1}{m_{2}} \nonumber \]

Кількість\(\mu\) відома як зменшена маса системи. Рівняння (13.1.7) тепер набуває вигляду

\[\overrightarrow{\mathbf{F}}_{2,1}=\mu \frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \nonumber \]

Робота, виконана в системі з витіснення двох мас з початкового стану А в кінцевий стан В, дається

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{1}+\int_{A}^{B} \overrightarrow{\mathbf{F}}_{1,2} \cdot d \overrightarrow{\mathbf{r}}_{2} \nonumber \]

Нагадаємо, по теоремі робочої енергії, що LHS - це робота, виконана над системою,

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{1}+\int_{A}^{B} \overrightarrow{\mathbf{F}}_{1,2} \cdot d \overrightarrow{\mathbf{r}}_{2}=\Delta K \nonumber \]

З третього закону Ньютона сума в рівнянні (13.1.10) стає

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{1}-\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{2}=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot\left(d \overrightarrow{\mathbf{r}}_{1}-d \overrightarrow{\mathbf{r}}_{2}\right)=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{2,1} \nonumber \]

де\(d \overrightarrow{\mathbf{r}}_{2,1}\) - відносне зміщення двох тіл. Тепер ми можемо замінити другий закон Ньютона, рівняння (13.1.9), для відносного прискорення в рівняння (13.1.12),

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{2,1}=\int_{A}^{B} \mu \frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \cdot d \overrightarrow{\mathbf{r}}_{2,1}=\mu \int_{A}^{B}\left(\frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t}\right) d t \nonumber \]

де ми використовували співвідношення між диференціальними елементами\(d{\mathbf{r}}_{2,1}=\frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} d t\). Правило добутку для похідних скалярного добутку вектора з самим собою дано для цього випадку

\[\frac{1}{2} \frac{d}{d t}\left(\frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t}\right)=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} \nonumber \]

Замініть рівняння (13.1.14) на рівняння (13.1.13), яке потім стає

\[W=\mu \int_{A}^{B} \frac{1}{2} \frac{d}{d t}\left(\frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t}\right) d t \nonumber \]

Рівняння (13.1.15) тепер є інтегралом точної похідної, що дає

\[W=\left.\frac{1}{2} \mu\left(\frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t}\right)\right|_{A} ^{B}=\left.\frac{1}{2} \mu\left(\overrightarrow{\mathbf{v}}_{2,1} \cdot \overrightarrow{\mathbf{v}}_{2,1}\right)\right|_{A} ^{B}=\frac{1}{2} \mu\left(v_{B}^{2}-v_{A}^{2}\right) \nonumber \]

де\(\overrightarrow{\mathbf{V}}_{2,1}\) - відносна швидкість між двома тілами. Важливо зазначити, що у вищезгаданій деривації, якби ми обмінялися ролями тіла 1 і 2, тобто\(1 \rightarrow 2 \text { and } 2 \rightarrow 1\) ми отримали б однаковий результат, тому що

\ [\ почати {вирівняний}
\ стрілка над праворуч {\ mathbf {F}} _ {1,2} &=-\ переправа {\ mathbf {F}} _ {2,1}\
\\ переправа стрілка {\ mathbf {r}} _ {1,2} &=\ переправа {\ mathbf {r}} _ {2} -\ переправа стрілка {\ mathbf {r}} _ {1} =-\ переправа стрілка {\ mathbf {r}} _ {2,1}\
d\ стрілка переходу {\ mathbf {r}} _ { 1,2} &= d\ ліворуч (\ переправа стрілка {\ mathbf {r}} _ {2} -\ переправа стрілка {\ mathbf {r}} _ {1}\ праворуч) =-d\ переправа стрілка {\ mathbf {r}}\\
\ переправа стрілка {\ mathbf {v}} _ {1,2} &=-\ переправа стрілка {\ mathbf {v}} _ {2,1}
\ кінець {вирівняний}\ nonumber\]

Рівняння (13.1.16) має на увазі, що виконана робота - це зміна кінетичної енергії системи, яку ми можемо записати через зменшену масу і зміну квадрата відносної швидкості двох об'єктів

\[\Delta K=\frac{1}{2} \mu\left(v_{B}^{2}-v_{A}^{2}\right) \nonumber \]