8.7: Опрацьовані приклади

Приклад 8.7 Сходи

Об'єкт масою m в момент t = 0 має швидкість$v_{0}$ Він ковзає відстань s по горизонтальному підлозі, а потім з вершини сходів (рис. 8.35). Коефіцієнт кінетичного тертя між об'єктом і підлогою -$\mu_{\mathrm{k}}$ Об'єкт б'є в дальній кінець третьої сходи. Кожна сходи має підйом h і прогін d. Нехтуйте опором повітря і використовуйте g для гравітаційної постійної. (а) Яка відстань s, на якій об'єкт ковзає по підлозі?

Малюнок 8.35 Об'єкт, що падає вниз по сходах

Рішення: Існує два різних етапи руху об'єкта, початковий горизонтальний рух, а потім вільне падіння. Задане кінцеве положення об'єкта, в дальньому кінці третьої сходи, визначить горизонтальну складову швидкості в той момент, коли об'єкт покинув вершину сходів. Це в свою чергу може бути використано для визначення часу сповільнення об'єкта уздовж підлоги, а значить і пройденого на підлозі відстані. Задані величини - m, v0, μk, g, h і d.

Для горизонтального руху виберіть координати з початковою позицією блоку. Виберіть позитивний$\hat{\mathbf{i}}$ напрямок, щоб бути горизонтальним, спрямованим вліво на малюнку 8.35,$\hat{\mathbf{j}}$ -напрямок, щоб бути вертикальним (вгору). Сили на об'єкт - це$m \overrightarrow{\mathbf{g}}=-m g \hat{\mathbf{j}}$ гравітація, нормальна сила$\overrightarrow{\mathbf{N}}=N \hat{\mathbf{j}}$ і кінетична сила тертя$\overrightarrow{\mathbf{f}}_{\mathrm{k}}=-f_{\mathrm{k}} \hat{\mathbf{i}}$. Складовими векторів у другому$\overrightarrow{\mathbf{F}}=m \overrightarrow{\mathbf{a}}$ законі Ньютона є

\ [\ почати {вирівняний}
-f_ {\ mathrm {k}} &=м a_ {x}\\
n-м g &=m a_ {y}
\ кінець {вирівняний}\ nonumber\]

Об'єкт не рухається у напрямку y;$a_{y}=0$ і, таким чином, з другого виразу в (8.6.19),$N=m g$ Величина сили тертя тоді$f_{\mathrm{k}}=\mu_{\mathrm{k}} N=\mu_{\mathrm{k}} m g$, і перший вираз в (8.6.19) дає x -компонент прискорення як$a_{x}=-\mu_{\mathrm{k}} g$ тому, що прискорення є постійним x - складова швидкості задається

$$v_{x}(t)=v_{0}+a_{x} t \nonumber$$

де$v_{0}$ - х -складова швидкості об'єкта, коли він тільки почав ковзати. Зсув задається

$$x(t)-x_{0}=v_{0} t+\frac{1}{2} a_{x} t^{2} \nonumber$$

Позначте час, коли блок просто покине посадку$t_{1}$, де$x\left(t_{1}\right)=s$ і швидкість якраз при досягненні приземлення$v_{x}\left(t_{1}\right)=v_{x, 1}$. Початкова швидкість -$v_{0}$ і$x_{0}=0$. Використовуючи початкові і кінцеві умови, і значення прискорення, Рівняння (8.6.21) стає

$$s=v_{0} t_{1}-\frac{1}{2} \mu_{k} g t_{1}^{2} \nonumber$$

Розв'яжіть Рівняння (8.6.20) за час, коли блок досягає краю посадки,

$$t_{1}=\frac{v_{x, 1}-v_{0}}{-\mu_{\mathrm{k}} g}=\frac{v_{0}-v_{x, 1}}{\mu_{\mathrm{k}} g} \nonumber$$

Заміна рівняння (8.6.23) на рівняння (8.6.22) дає

$$s=v_{0}\left(\frac{v_{0}-v_{x, 1}}{\mu_{\mathrm{k}} g}\right)-\frac{1}{2} \mu_{k} g\left(\frac{v_{0}-v_{x, 1}}{\mu_{\mathrm{k}} g}\right)^{2} \nonumber$$

і після деякої алгебри ми можемо переписати рівняння (8.6.24) як

$$s=\frac{v_{0}^{2}-v_{x, 1}^{2}}{2 \mu_{\mathrm{k}} g} \nonumber$$

Від вершини сходів до дальнього кінця третьої сходи об'єкт знаходиться у вільному падінні. Виберіть позитивний$\hat{\mathbf{i}}$ -напрямок, щоб бути горизонтальним, спрямованим вліво на малюнку 8.35, а позитивний$\hat{\mathbf{j}}$ -напрямок - вертикальним (вгору) і тепер виберіть початок у верхній частині сходів, де об'єкт спочатку йде у вільне падіння. Компонентами прискорення є$a_{x}=0$$a_{y}=-g$, початкова x -складова швидкості є$v_{x, 1}$, початкова y -складова швидкості є$v_{y, 0}=0$, початкова x -позиція є$x_{0}=0$ і початкова y -позиція є$y_{0}=0$. Скидання,$t=0$ коли об'єкт просто залишає сходову площадку. Нехай$t_{2}$ позначають момент потрапляння об'єкта на сходи, де$y\left(t_{2}\right)=-3 h$ і$x\left(t_{2}\right)=3 d$. Рівняння, що описують положення і швидкість об'єкта в часі$t=t_{2}$, є

$$x\left(t_{2}\right)=3 d=v_{x, 1} t_{2} \nonumber$$

$$y\left(t_{2}\right)=-3 h=-\frac{1}{2} g t_{2}^{2} \nonumber$$

Розв'яжіть рівняння (8.6.26) для$t_{2}$ отримання прибутку

$$t_{2}=\frac{3 d}{v_{x, 1}} \nonumber$$

Замініть рівняння (8.6.28) у рівняння (8.6.27) та усуньте змінну$t_{2}$

$$3 h=\frac{1}{2} g \frac{9 d^{2}}{v_{x, 1}^{2}} \nonumber$$

Рівняння (8.6.29) тепер можна вирішити для квадрата горизонтальної складової швидкості,

$$v_{x, 1}^{2}=\frac{3 g d^{2}}{2 h} \nonumber$$

Тепер замініть Рівняння (8.6.30) у Рівняння (8.6.25), щоб визначити відстань, яку об'єкт пройшов на посадці,

$$s=\frac{v_{0}^{2}-\left(3 g d^{2} / 2 h\right)}{2 \mu_{\mathrm{k}} g} \nonumber$$

Приклад 8.8 Переміщення кошика по доріжці

Малюнок 8.36 Падаючий блок прискорить візок на доріжці за допомогою тягового зусилля струни. Датчик сили вимірює натяг в струні.

Розглянемо візок, який вільно ковзає по горизонтальній доріжці (рис. 8.36). Зусилля прикладається до візка через струну, яка прикріплена до датчика сили, встановленого на візку, обмотується навколо шківа і прикріплена до блоку на іншому кінці. Коли блок буде звільнений, візок почне прискорюватися. Датчик сили і візок разом мають масу$m_{\mathrm{C}}$, а підвішений блок має масу$m_{\mathrm{B}}$. Нехтуйте невеликою масою струни і шківа, і припускайте, що струна нерозтягується. Коефіцієнт кінетичного тертя між візком і колією дорівнює$\mu_{\mathrm{k}}$. Визначити (i) прискорення візка, і (ii) натяг в струні.

Рішення: Загалом, ми хотіли б намалювати діаграми вільного тіла на всіх окремих об'єктах (візок, датчик, шків, мотузка та блок), але ми також можемо вибрати систему, що складається з двох (або більше) об'єктів, знаючи, що сили взаємодії між будь-якими двома об'єктами скасуються попарно Третім законом Ньютона. У цьому прикладі ми виберемо датчик/візок як одне вільне тіло, а блок як інше вільне тіло. Діаграма сили вільного тіла для датчика/візка показана на малюнку 8.37.

Малюнок 8.37 Діаграма сили на датчику/візку з векторним розкладанням контактної сили на горизонтальну і вертикальну складові

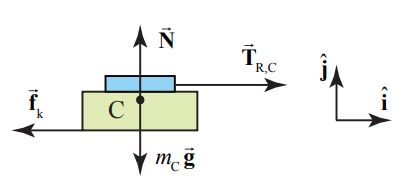
На датчик/візок діють три сили: гравітаційна сила$m_{\mathrm{C}} \overrightarrow{\mathbf{g}}$, сила$\overrightarrow{\mathbf{T}}_{\mathrm{R}, \mathrm{C}}$ тяги мотузки на датчику сили та сила контакту між колією та візком. На малюнку 8.34 ми розкладаємо контактну силу на дві її складові - кінетичну силу тертя$\overrightarrow{\mathbf{f}}_{\mathrm{k}}=-f_{\mathrm{k}} \hat{\mathbf{i}}$ і нормальну силу,$\overrightarrow{\mathbf{N}}=N \hat{\mathbf{j}}$.

Візок прискорюється лише в горизонтальному напрямку,$\overrightarrow{\mathbf{a}}_{\mathrm{C}}=a_{\mathrm{C} x} \hat{\mathbf{i}}$ тому складова сили у вертикальному напрямку повинна бути нульовою$a_{\mathrm{C}_{y}}=0$. Тепер ми можемо застосувати Другий закон Ньютона в горизонтальному і вертикальному напрямках і знайти, що

$$\hat{\mathbf{i}}: T_{\mathrm{R}, \mathrm{C}}-f_{\mathrm{k}}=m_{\mathrm{C}} a_{\mathrm{C}, x} \nonumber$$

$$\hat{\mathbf{j}}: \quad N-m_{\mathrm{C}} g=0 \nonumber$$

З Рівняння (8.6.33) робимо висновок, що нормальною складовою є

$$N=m_{\mathrm{C}} g \nonumber$$

Ми використовуємо рівняння (8.6.34) для нормальної сили, щоб знайти, що величина кінетичної сили тертя дорівнює

$$f_{\mathrm{k}}=\mu_{\mathrm{k}} N=\mu_{\mathrm{k}} m_{\mathrm{c}} g \nonumber$$

Тоді рівняння (8.6.32) стає

$$T_{\mathrm{R}, \mathrm{C}}-\mu_{\mathrm{k}} m_{\mathrm{C}} g=m_{\mathrm{C}} a_{\mathrm{C}, x} \nonumber$$

Схема сили для блоку показана на малюнку 8.38. Дві сили, що діють на блок, - це$\overrightarrow{\mathbf{T}}_{\mathrm{R}, \mathrm{B}}$ сила тяги струни і сила тяжіння$m_{\mathrm{B}} \overrightarrow{\mathbf{g}}$. Тепер ми застосуємо Другий закон Ньютона до блоку і знаходимо, що

$$\hat{\mathbf{J}}_{\mathrm{B}}: m_{\mathrm{B}} g-T_{\mathrm{R}, \mathrm{B}}=m_{\mathrm{B}} a_{B, y} \nonumber$$

Малюнок 8.38 Сили, що діють на блок

У Рівнянні (8.6.37) символ$a_{B, y}$ представляє складову прискорення зі знаком, визначеним нашим вибором напрямку вниз для одиничного вектора$\hat{\mathbf{j}}_{\mathrm{B}}$. Зауважимо, що ми зробили інший вибір напрямку для вектора одиниці у вертикальному напрямку на діаграмі вільного тіла для блоку, показаного на малюнку 8.37. Кожна діаграма вільного тіла має незалежний набір одиничних векторів, які визначають знак умовності для векторного розкладання сил, що діють на вільне тіло, і прискорення вільного тіла. У нашому прикладі, з одиничним вектором, спрямованим вниз на малюнку 8.38, якщо ми вирішуємо для складової прискорення і вона позитивна, то ми знаємо, що напрямок прискорення - вниз.

Існує другий тонкий спосіб введення знаків щодо сил, що діють на вільне тіло. У нашому прикладі сила між струною і блоком, що діє на блок, вказує вгору, тому при векторному розкладанні сил, що діють на блок, що з'являється на лівій стороні Рівняння (8.6.37), ця сила має знак мінус і величину,$\overrightarrow{\mathbf{T}}_{\mathrm{R}, \mathrm{B}}=-T_{\mathrm{R}, \mathrm{B}} \hat{\mathbf{j}}_{\mathrm{B}}$ де$T_{\mathrm{R}, \mathrm{B}}$ приймається позитивним.

Наше припущення про те, що маса мотузки і маса шківа мізерно малі, дозволяє стверджувати, що натяг в мотузці рівномірне і за величиною дорівнює силам на кожному кінці мотузки,

$$T_{\mathrm{R}, \mathrm{B}}=T_{\mathrm{R}, \mathrm{C}} \equiv T \nonumber$$

Ми також припустили, що струна нерозтягується (не розтягується). Це означає, що мотузка, блок та датчик/візок мають однакову величину прискорення,

$$a_{\mathrm{C}, x}=a_{\mathrm{B}, y} \equiv a \nonumber$$

Використовуючи рівняння (8.6.38) та (8.6.39), тепер ми можемо переписати рівняння руху для датчика/кошика, рівняння (8.6.36), як

$$T-\mu_{\mathrm{k}} m_{\mathrm{C}} g=m_{\mathrm{C}} a \nonumber$$

і рівняння руху (8.6.37) для блоку як

$$m_{\mathrm{B}} g-T=m_{\mathrm{B}} a \nonumber$$

У нас є тільки два невідомих T і a, тому тепер ми можемо вирішити два рівняння (8.6.40) і (8.6.41) одночасно для прискорення датчика/візка і натягу в мотузці. Спочатку вирішуємо Рівняння (8.6.40) для натягу

$$T=\mu_{\mathrm{k}} m_{\mathrm{C}} g+m_{\mathrm{C}} a \nonumber$$

а потім підставити рівняння (8.6.42) на рівняння (8.6.41) і знайти, що

$$m_{\mathrm{B}} g-\left(\mu_{\mathrm{k}} m_{\mathrm{C}} g+m_{\mathrm{C}} a\right)=m_{\mathrm{B}} a \nonumber$$

Тепер ми можемо вирішити рівняння (8.6.43) для прискорення,

$$a=\frac{m_{\mathrm{B}} g-\mu_{\mathrm{k}} m_{\mathrm{C}} g}{m_{\mathrm{C}}+m_{\mathrm{B}}} \nonumber$$

Заміна рівняння (8.6.44) на рівняння (8.6.42) дає напругу в струні,

\ [\ почати {вирівнювання}
T &=\ mu_ {\ mathrm {k}} m_ {\ mathrm {C}} g+m_ {\ mathrm {C}} a\\
&=\ mu_ {\ mathrm {k}} m_ {\ математика {C}} g+m_ {\ mathrm {C}\ математика {B}} g-\ mu_ {\ mathrm {k}} m_ {\ математика {C}} г} {m_ {\ mathrm {C}} +m_ {\ mathrm {B}}\\
&=\ ліворуч (\ mu_ {\ mathrm {k}} +1\ праворуч)\ frac {m_ {\ mathrm {C}} m_ {\ mathrm {B}}} {m_ {\ mathrm {C}} +m_ {\ mathrm {B}} г
\ кінець {вирівняний}\ номер\]

У цьому прикладі ми застосували Другий закон Ньютона до двох об'єктів: один складний об'єкт, що складається з датчика і візка, а інший блок. Ми проаналізували сили, що діють на кожен об'єкт, а також будь-які обмеження, накладені на прискорення кожного об'єкта. Ми використовували силові закони для кінетичного тертя та гравітації на кожній системі вільного тіла. Три рівняння руху дозволяють визначити сили, які залежать від параметрів у прикладі: напруга в мотузці, прискорення предметів і нормальна сила між візком і столом.

Приклад 8.9 Умови обмеження шківів та канатів

Розглянемо розташування шківів і блоків, показане на малюнку 8.39. Шківи приймаються безмасовими і без тертя, а сполучні струни - безмасовими і нерозтяжними. Позначте відповідні маси блоків as$m_{1}$$m_{2}$, і$m_{3}$. Верхній шків на малюнку вільно обертається, але його центр маси не рухається. Обидва шківа мають однаковий радіус R. (a) Як пов'язані прискорення об'єктів? (b) Намалюйте діаграми сили на кожному рухомому об'єкті. (c) Вирішити для прискорення об'єктів і напруженості в мотузках.

Малюнок 8.39 Система обмеженого шківа

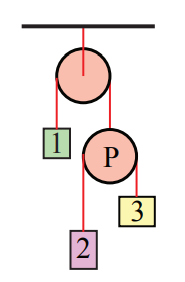
Рішення: (а) Виберіть початок у центрі верхнього шківа. Ввести координатні функції для трьох рухомих блоків,$y_{1}$,$y_{2}$, і$y_{3}$. Ввести координатну функцію\ begin {equation} y_ {P}\ end {рівняння} для рухомого шківа (шків праворуч внизу на рис. 8.40). Виберіть вниз для позитивного напрямку; система координат показана на малюнку нижче.

Малюнок 8.40 Скоординована система для системи шківів

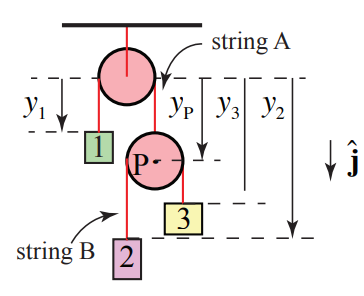
Довжина рядка A задається

$$l_{A}=y_{1}+y_{P}+\pi R \nonumber$$

де$\pi R$ - довжина дуги мотузки, що контактує зі шківом. Ця довжина постійна, і тому друга похідна по часу дорівнює нулю,

$$0=\frac{d^{2} l_{A}}{d t^{2}}=\frac{d^{2} y_{1}}{d t^{2}}+\frac{d^{2} y_{P}}{d t^{2}}=a_{y, 1}+a_{y, P} \nonumber$$

При цьому блок 1 і рухомий шків компоненти прискорення рівні за величиною, але протилежні за знаком,

$$a_{y, P}=-a_{y, 1} \nonumber$$

Довжина рядка B задається

$$l_{B}=\left(y_{3}-y_{p}\right)+\left(y_{2}-y_{p}\right)+\pi R=y_{3}+y_{2}-2 y_{P}+\pi R \nonumber$$

де$\pi R$ - довжина дуги мотузки, що контактує зі шківом. Ця довжина також постійна, тому друга похідна по часу дорівнює нулю,

$$0=\frac{d^{2} l_{B}}{d t^{2}}=\frac{d^{2} y_{2}}{d t^{2}}+\frac{d^{2} y_{3}}{d t^{2}}-2 \frac{d^{2} y_{p}}{d t^{2}}=a_{y, 2}+a_{y, 3}-2 a_{y, P} \nonumber$$

Ми можемо замінити рівняння (8.6.48) для прискорення шківа в Рівняння (8.6.50), що дає зв'язок обмеження між складовими прискорення трьох блоків,

$$0=a_{y, 2}+a_{y, 3}+2 a_{y, 1} \nonumber$$

б) Діаграми сили вільного тіла: сили, що діють на блок 1, є: гравітаційна сила$m_{1} \overrightarrow{\mathbf{g}}$ і сила тяги$\overrightarrow{\mathbf{T}}_{A, 1}$ струни А, що діє на блок 1. Позначте величину цієї сили$T_{A}$ тим, що тятива приймається безмасовою і шків приймається безмасовим і нефрикційним, натяг$T_{A}$ в струні рівномірний і за величиною дорівнює тяговому зусиллю струни на блоці. Схема вільного тіла на блоці 1 показана на малюнку 8.41 (а).

Малюнок 8.41 Діаграма сили вільного тіла на (а) блоці 1; (б) блок 2; (в) блок 3; (г) шків

Другий закон Ньютона, застосований до блоку 1, тоді

$$\hat{\mathbf{j}}: m_{1} g-T_{A}=m_{1} a_{y, 1} \nonumber$$

Сили на блоці 2 - це гравітаційна сила$m_{2} \overrightarrow{\mathbf{g}}$ і струна В, що утримує блок$\overrightarrow{\mathbf{T}}_{B, 2}$, з величиною$T_{B}$. Діаграма вільного тіла для сил, що діють на блок 2, показана на малюнку 8.41 (б). Другий закон Ньютона, застосований до блоку 2,

$$\hat{\mathbf{j}}: m_{2} g-T_{B}=m_{2} a_{y, 2} \nonumber$$

Сили на блоці 3 є гравітаційною силою$m_{3} \overrightarrow{\mathbf{g}}$ і струною, що утримує блок$\overrightarrow{\mathbf{T}}_{B, 3}$, з величиною, рівною$T_{B}$ тому, що шків Р приймається як безтертя, так і безмасовим. Діаграма вільного тіла для сил, що діють на блок 3, показана на малюнку 8.41 (в). Другий закон Ньютона, застосований до блоку 3,

$$\hat{\mathbf{j}}: m_{3} g-T_{B}=m_{3} a_{y, 3} \nonumber$$

Сили на рухомому шківі Р - сила гравітації$m_{P} \overrightarrow{\mathbf{g}}=\overrightarrow{\mathbf{0}}$ (шків приймається безмасовим); струна В тягне вниз по шківу з кожного боку з силою,$\overrightarrow{\mathbf{T}}_{B, P}$ яка має величину$T_{B}$. Струна А утримує шків вгору з силою$\overrightarrow{\mathbf{T}}_{A, P}$ з величиною,$T_{A}$ рівною натягу в струні А. Діаграма вільного тіла для сил, що діють на рухомий шків, показана на малюнку 8.41 (г). Другий закон Ньютона, застосований до шківа

$$\hat{\mathbf{j}}: 2 T_{B}-T_{A}=m_{P} a_{y, P}=0 \nonumber$$

Оскільки шків вважається безмасовим, ми можемо використовувати це останнє рівняння, щоб визначити умову, що напруга в двох струн повинна задовольняти,

$$2 T_{B}=T_{A} \nonumber$$

Тепер ми в змозі визначити прискорення блоків і натяг в двох струн. Записуємо відповідні рівняння у вигляді резюме.

$$0=a_{y, 2}+a_{y, 3}+2 a_{y, 1} \nonumber$$

$$m_{1} g-T_{A}=m_{1} a_{y, 1} \nonumber$$

$$m_{2} g-T_{B}=m_{2} a_{y, 2} \nonumber$$

$$m_{3} g-T_{B}=m_{3} a_{y, 3} \nonumber$$

$$2 T_{B}=T_{A} \nonumber$$

Існує п'ять рівнянь з п'ятьма невідомими, тому ми можемо вирішити цю систему. Спочатку ми використаємо рівняння (8.6.61), щоб усунути напругу$T_{A}$ в рівнянні (8.6.58), що дає

$$m_{1} g-2 T_{B}=m_{1} a_{y, 1} \nonumber$$

Тепер ми вирішуємо рівняння (8.6.59), (8.6.60) і (8.6.62) для прискорень,

$$a_{y, 2}=g-\frac{T_{B}}{m_{2}} \nonumber$$

$$a_{y, 3}=g-\frac{T_{B}}{m_{3}} \nonumber$$

$$a_{y, 1}=g-\frac{2 T_{B}}{m_{1}} \nonumber$$

Тепер ми підставляємо ці результати для прискорень у рівняння обмеження, Рівняння (8.6.57),

$$0=g-\frac{T_{B}}{m_{2}}+g-\frac{T_{B}}{m_{3}}+2 g-\frac{4 T_{B}}{m_{1}}=4 g-T_{B}\left(\frac{1}{m_{2}}+\frac{1}{m_{3}}+\frac{4}{m_{1}}\right) \nonumber$$

Тепер ми можемо вирішити це останнє рівняння для натягу в рядку B,

$$T_{B}=\frac{4 g}{\left(\frac{1}{m_{2}}+\frac{1}{m_{3}}+\frac{4}{m_{1}}\right)}=\frac{4 g m_{1} m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber$$

З Рівняння (8.6.61) напруга в струні А дорівнює

$$T_{A}=2 T_{B}=\frac{8 g m_{1} m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber$$

Знаходимо прискорення блоку 1 з Рівняння (8.6.65), використовуючи Рівняння (8.6.67) для натягу в струні B,

$$a_{y, 1}=g-\frac{2 T_{B}}{m_{1}}=g-\frac{8 g m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}}=g \frac{m_{1} m_{3}+m_{1} m_{2}-4 m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber$$

Знаходимо прискорення блоку 2 з Рівняння (8.6.63), використовуючи Рівняння (8.6.67) для натягу в струні B,

$$a_{y, 2}=g-\frac{T_{B}}{m_{2}}=g-\frac{4 g m_{1} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}}=g \frac{-3 m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber$$

Аналогічно знаходимо прискорення блоку 3 з Рівняння (8.6.64), використовуючи Рівняння (8.6.67) для натягу в струні B,

$$a_{y, 3}=g-\frac{T_{B}}{m_{3}}=g-\frac{4 g m_{1} m_{2}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}}=g \frac{m_{1} m_{3}-3 m_{1} m_{2}+4 m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber$$

В якості перевірки на нашу алгебру відзначимо, що

\ [\ begin {масив} {l}
2 a_ {1, y} +a_ {2, y} +a_ {3, y} =\\
2 г\ frac {m_ {1} m_ {3} +m_ {2} -4 m_ {2} m_ {3}} {m_ {1} m_ {3} _ {2} +4 м_ {2} м_ {3}} +г\ фракція {-3 м_ {1} м_ {3} +м_ {1} м_ {2} +4 м_ {2} м_ {3}} {м_ {1} м_ {3} +м_ {1} м_ {2} +4 м_ {2} м_ {3}} +4 м_ {2} м_ {3}} +4 м_ {3}} +4 м_ {3} c {m_ {1} м_ {3} -3 м_ {1} м_ {2} +4 м_ {2} м_ {3}} {m_ {1} m_ {3} +m_ {1} m_ {2} +4 m_ {2} m_ {3}}\\
=0
\ end {масив}\ nonumber\]

Приклад 8.10 Прискорення клина

Малюнок 8.42 Блок на прискорювальному клині

45o клин висувається вздовж столу з постійним прискоренням$\overrightarrow{\mathbf{A}}$ відповідно до спостерігача в стані спокою щодо столу. Блок масою m ковзає без тертя вниз по клину (рис. 8.42). Знайдіть його прискорення щодо спостерігача в стані спокою щодо столу. Запишіть план знаходження величини прискорення блоку. Переконайтеся, що ви чітко вказуєте, які концепції ви плануєте використовувати для обчислення будь-яких відповідних фізичних величин. Також чітко викладіть будь-які припущення, які ви робите. Переконайтеся, що ви додали будь-які діаграми сили вільного тіла або ескізи, які ви плануєте використовувати.

Рішення: Виберіть систему координат блоку і клина, як показано на малюнку 8.43. Тоді$\overrightarrow{\mathbf{A}}=A_{x, w} \hat{\mathbf{i}}$ де$A_{x, w}$ - х-складова прискорення клина.

Малюнок 8.43 Система координат блоку на прискорювальному клині

Ми застосуємо Другий закон Ньютона до блоку, що ковзає вниз по клину. Оскільки клин прискорюється, існує залежність між x - і y - складовими прискорення блоку. Для того, щоб знайти це обмеження, ми вибираємо систему координат для клину та блоку, що ковзає вниз по клину, показаному на малюнку нижче. Ми знайдемо залежність обмежень між складовими прискорень блоку і клина геометричним аргументом. З малюнка вище ми бачимо, що

$$\tan \phi=\frac{y_{b}}{l-\left(x_{b}-x_{w}\right)} \nonumber$$

Тому

$$y_{b}=\left(l-\left(x_{b}-x_{w}\right)\right) \tan \phi \nonumber$$

Якщо ми диференціюємо рівняння (8.6.73) двічі щодо часу, зазначивши, що

$$\frac{d^{2} l}{d t^{2}}=0 \nonumber$$

ми маємо, що

$$\frac{d^{2} y_{b}}{d t^{2}}=-\left(\frac{d^{2} x_{b}}{d t^{2}}-\frac{d^{2} x_{w}}{d t^{2}}\right) \tan \phi \nonumber$$

Тому

$$a_{b, y}=-\left(a_{b, x}-A_{x, w}\right) \tan \phi \nonumber$$

де

$$A_{x, w}=\frac{d^{2} x_{w}}{d t^{2}} \nonumber$$

Тепер намалюємо схему сили вільного тіла для блоку (рис. 8.44). Другий закон Ньютона в$\hat{\mathbf{i}}$ - напрямку стає

$$N \sin \phi=m a_{b x} \nonumber$$

і$\hat{\mathbf{j}}$ -напрямок стає

$$N \cos \phi-m g=m a_{b, y} \nonumber$$

Малюнок 8.44 Діаграма сили вільного тіла на блоці

Ми можемо вирішити для нормальної сили з Рівняння (8.6.78):

$$N=\frac{m a_{b, x}}{\sin \phi} \nonumber$$

Тепер ми замінюємо рівняння (8.6.76) та рівняння (8.6.80) на рівняння (8.6.79), що дає

$$\frac{m a_{b, x}}{\sin \phi} \cos \phi-m g=m\left(-\left(a_{b, x}-A_{w, x}\right) \tan \phi\right) \nonumber$$

Тепер ми прибираємо це врожайність

$$m a_{b, x}(\operatorname{cotan} \phi+\tan \phi)=m\left(g+A_{w, x} \tan \phi\right) \nonumber$$

Таким чином, x-складова прискорення тоді

$$a_{b, x}=\frac{g+A_{w, x} \tan \phi}{\operatorname{cotan} \phi+\tan \phi} \nonumber$$

З Рівняння (8.6.76), y -складова прискорення

$$a_{b, y}=-\left(a_{b, x}-A_{w, x}\right) \tan \phi=-\left(\frac{g+A_{w, x} \tan \phi}{\operatorname{cotan} \phi+\tan \phi}-A_{w, x}\right) \tan \phi \nonumber$$

Це спрощує

$$a_{b, y}=\frac{A_{w, x}-g \tan \phi}{\operatorname{cotan} \phi+\tan \phi} \nonumber$$

Коли$\phi=45^{\circ}$, cotan$45^{\circ}=\tan 45^{\circ}=1$, і так Рівняння (8.6.83) стає

$$a_{b, x}=\frac{g+A_{w, x}}{2} \nonumber$$

і рівняння (8.6.85) стає

$$a_{b, y}=\frac{A-g}{2} \nonumber$$

Величина прискорення тоді

\ [\ почати {вирівняний}
a=\ sqrt {a_ {b, x} ^ {2} +a_ {b, y} ^ {2}} &=\ sqrt {\ ліворуч (\ frac {g+a_ {w x}}} {2}\ праворуч) ^ {2} +\ вліво (\ frac {A_ {w x} -g} {2}\ праворуч) ^ {2} +\ вліво (\ frac {A_ {w x} -g} {2}\ праворуч) ^ {2} +\ вліво (\ frac {
A 2}}\ a &=\ sqrt {\ ліворуч (\ frac {g^ {2} +A_ {w} ^ {2}} {2}\ праворуч)}
\ кінець {вирівняний}\ nonumber\]

Приклад 8.11: Капістан

Пристрій під назвою капстан використовується на борту кораблів для того, щоб контролювати мотузку, яка знаходиться під великим натягом. Канат обмотується навколо нерухомого барабана радіусом R, як правило, на кілька витків (на рис. 8.45 показано близько трьох четвертих обороту, як видно з верхнього боку). Навантаження на мотузку тягне її з силою$T_{A}$ і матрос утримує інший кінець мотузки з набагато меншою силою$T_{B}$. Коефіцієнт статичного тертя між мотузкою і барабаном дорівнює$\mu_{\mathrm{s}}$. Моряк тримає мотузку так, що вона ось-ось зісковзне. Покажіть,$T_{B}=T_{A} e^{-\mu_{s} \theta_{B A}}$ де$\theta_{B A}$ знаходиться кут, підтягнутий мотузкою на барабані.

Малюнок 8.47. Правий край зрізу знаходиться під кутом θ, а лівий край зрізу знаходиться під$\theta+\Delta \theta$ кутовим краєм кінця зрізу робить з горизонтальним є$\Delta \theta / 2$. На цю ділянку мотузки діють чотири сили. Сили - це нормальна сила між капістаном і мотузкою, спрямованою назовні, статичною силою тертя та напругою на будь-якому кінці зрізу. Мотузка тримається в точці просто ковзання, тому, якщо навантаження надасть більшу силу, мотузка зісковзне вправо. Тому напрямок статичної сили тертя між капстаном і мотузкою, що діє на мотузку, вказує вліво. Натяг на правій стороні зрізу позначається знаком$T(\theta) \equiv T$, при цьому натяг на лівій стороні зрізу позначається$T(\theta+\Delta \theta) \equiv T+\Delta T$. Чи збільшується напруга в цьому зрізі з правого боку на ліву, збільшується, залишається колишнім або зменшується? Напруга зменшується через те, що навантаження з лівого боку менше, ніж навантаження з правого боку. Зауважте, що$\Delta T<0$.

Малюнок 8.47 Діаграма сили вільного тіла на малому шматочку мотузки

Векторне розкладання сил задається

$$\hat{\mathbf{i}}: T \cos (\Delta \theta / 2)-f_{s}-(T+\Delta T) \cos (\Delta \theta / 2) \nonumber$$

$$\hat{\mathbf{j}}:-T \sin (\Delta \theta / 2)+N-(T+\Delta T) \sin (\Delta \theta / 2) \nonumber$$

Для малих кутів$\Delta \theta$$\cos (\Delta \theta / 2) \cong 1$, і$\sin (\Delta \theta / 2) \cong \Delta \theta / 2$ Використовуючи малі кутові наближення, векторне розкладання сил у напрямку x ($\hat{\mathbf{i}}$напрямок) стає

\ [\ почати {вирівняний}
T\ cos (\ Дельта\ тета/2) -f_ {s} - (Т+\ Дельта Т)\ cos (\ Дельта\ тета/2) &\ simeq T-f_ {s} - (Т+\ Дельта Т)\\
&=-f_ {s} -\ Дельта Т
\ кінець {вирівняний}\ nonumber\]

За умовою статичної рівноваги сума х -складових сил дорівнює нулю,

$$-f_{\mathrm{s}}-\Delta T=0 \nonumber$$

Векторне розкладання сил у -напрямку ($+\hat{\mathbf{j}}$-напрямок) приблизно

\ [\ почати {вирівняний}
-T\ sin (\ Дельта\ тета/2) +N- (Т+\ Дельта Т)\ sin (\ Дельта\ тета/2) &\ simeq-t\ Дельта\ тета/2+N- (Т+\ Дельта Т)\ Дельта\ тета/2\
&= -T\ Theta\ Ta+N-\ Дельта Т\ дельта
\ тета/2\ кінець {}\ номер\]

В останньому рівнянні вище ми можемо ігнорувати терміни, пропорційні$\Delta T \Delta \theta$ тому, що вони є добутком двох малих величин і, отже, набагато менші, ніж члени, пропорційні$\Delta T$ або$\Delta \theta$. Векторне розкладання у напрямку y стає

$$-T \Delta \theta+N \nonumber$$

Статична рівновага має на увазі, що ця сума y -складових сил дорівнює нулю,

$$-T \Delta \theta+N=0 \nonumber$$

Ми можемо вирішити це рівняння для величини нормальної сили

$$N=T \Delta \theta \nonumber$$

Просто умова ковзання полягає в тому, що величина статичного тертя досягає свого максимального значення.

$$f_{\mathrm{s}}=\left(f_{\mathrm{s}}\right)_{\max }=\mu_{\mathrm{s}} N \nonumber$$

Тепер ми можемо об'єднати рівняння (8.6.92) і (8.6.97), щоб отримати

$$\Delta T=-\mu_{s} N \nonumber$$

Тепер підставляємо величину нормальної сили, Рівняння (8.6.96), в Рівняння (8.6.98), даючи

$$-\mu_{s} T \Delta \theta-\Delta T=0 \nonumber$$

Нарешті, вирішити це рівняння для відношення зміни натягу до зміни кута,

$$\frac{\Delta T}{\Delta \theta}=-\mu_{\mathrm{s}} T \nonumber$$

Похідна натягу по відношенню до кута θ визначається як межа

$$\frac{d T}{d \theta} \equiv \lim _{\Delta \theta \rightarrow 0} \frac{\Delta T}{\Delta \theta} \nonumber$$

і Рівняння (8.6.100) стає

$$\frac{d T}{d \theta}=-\mu_{s} T \nonumber$$

Це приклад лінійного диференціального рівняння першого порядку, яке показує, що швидкість зміни натягу щодо кута θ пропорційна негативу напруги під цим кутом θ. Це рівняння може бути вирішено шляхом інтеграції з використанням техніки поділу змінних. Спочатку ми переписуємо рівняння (8.6.102) як

$$\frac{d T}{T}=-\mu_{s} d \theta \nonumber$$

Інтегруйте обидві сторони, зазначивши, що коли θ = 0, натяг дорівнює силі навантаження,$T_{A}$ а коли кут$\theta=\theta_{A, B}$ натягу дорівнює$T_{B}$ силі, яку моряк прикладає до мотузки,

$$\int_{T=T_{A}}^{T=T_{B}} \frac{d T}{T}=-\int_{\theta=0}^{\theta=\theta_{B A}} \mu_{s} d \theta \nonumber$$

Результатом інтеграції є

$$\ln \left(\frac{T_{B}}{T_{A}}\right)=-\mu_{s} \theta_{B A} \nonumber$$

Зверніть увагу, що експоненціальна натурального логарифма

$$\exp \left(\ln \left(\frac{T_{B}}{T_{A}}\right)\right)=\frac{T_{B}}{T_{A}} \nonumber$$

отже, експонентірованіе обох сторін рівняння (8.6.105) дає

$$\frac{T_{B}}{T_{A}}=e^{-\mu_{\mathrm{s}} \theta_{B A}} \nonumber$$

напруга зменшується експоненціально,

$$T_{B}=T_{A} e^{-\mu_{s} \theta_{B A}} \nonumber$$

Оскільки напруга зменшується експоненціально, матросу потрібно лише застосувати невелику силу, щоб запобігти ковзанню мотузки.

Приклад 8.12 Вільне падіння з повітряним перетягуванням

Розглянемо об'єкт масою m, який знаходиться у вільному падінні, але відчуває опір повітря. Величина сили опору задається рівнянням (8.6.1), де$\rho$ - щільність повітря, А - площа поперечного перерізу предмета в площині, перпендикулярній руху, і$C_{D}$ коефіцієнт опору. Припустимо, що об'єкт звільнений від спокою і дуже швидко досягає швидкості, в якій застосовується рівняння (8.6.1). Визначте (i) кінцеву швидкість і (ii) швидкість об'єкта як функцію часу.

Рішення: Виберіть позитивний напрямок y вниз з початковою позицією об'єкта, як показано на малюнку 8.48 (a).

Малюнок 8.48 (a) Система координат для мармуру; (б) діаграма сили вільного тіла на мармурі

Існують дві сили, що діють на об'єкт: гравітаційна сила та сила опору, яка задається рівнянням (8.6.1). Схема вільного тіла показана на малюнку 8.48 (б). Другий закон Ньютона тоді

$$m g-(1 / 2) C_{D} A \rho v^{2}=m \frac{d v}{d t} \nonumber$$

Набір$\beta=(1 / 2) C_{D} A \rho$. Другий закон Ньютона потім можна записати як

$$m g-\beta v^{2}=m \frac{d v}{d t} \nonumber$$

Спочатку, коли об'єкт щойно звільняється з v = 0, опір повітря дорівнює нулю, а прискорення dv/dt максимальне. Коли об'єкт збільшує свою швидкість, опір повітря стає більшим і dv/dt зменшується, поки об'єкт не досягне кінцевої швидкості і dv/dt = 0. Встановіть dv/dt = 0 в Рівнянні (8.6.15) і вирішіть для кінцевої швидкості отримання.

$$v_{\infty}=\sqrt{\frac{m g}{\beta}}=\sqrt{\frac{2 m g}{C_{D} A \rho}} \nonumber$$

Значення величини кінцевої швидкості наведені в таблиці 8.3 для безлічі об'єктів з однаковим коефіцієнтом опору$C_{D}=0.5$

Таблиця 8.3 Швидкості терміналів для об'єктів різного розміру з$C_{D}=0.5$

Для інтеграції Equation (8.6.15) застосуємо методику поділу змінних та інтеграції частковими дробами. Спочатку перепишіть рівняння (8.6.15) як

$$\frac{-\beta}{m} d t=\frac{d v}{\left(v^{2}-\frac{m g}{\beta}\right)}=\frac{d v}{\left(v^{2}-v_{\infty}^{2}\right)}=\left(-\frac{1}{2 v_{\infty}\left(v+v_{\infty}\right)}+\frac{1}{2 v_{\infty}\left(v-v_{\infty}\right)}\right) d v \nonumber$$

Тоді інтегральний вираз рівняння (8.6.112)

$$-\int_{v^{\prime}=0}^{v^{\prime}=v(t)} \frac{d v^{\prime}}{2 v_{\infty}\left(v^{\prime}+v_{\infty}\right)}+\int_{v=0}^{v=v(t)} \frac{d v^{\prime}}{2 v_{\infty}\left(v^{\prime}-v_{\infty}\right)}=-\frac{\beta}{m} \int_{t=0}^{t^{\prime}=t} d t^{\prime} \nonumber$$

Інтеграція прибутковості

\ [\ begin {масив} {l}
-\ int_ {v^ {\ прайм} =0} ^ {v^ {\ прайм} =v (t)}\ frac {d v^ {\ прайм}} {\ прайм} {\ прайм}} ^ {v^ {\ прайм} =v (t)}\ frac {d v^ {\ прайм}} {2 v_ {\ infty}\ лівий (v^ {\ прайм} -v_ {\ infty}\ праворуч)} =-\ frac {\ бета^ {t^ {\ прайм} =t}} {м}\ int_ {t^ {\ прайм}} {t} d t^ {\ прайм }\
\ frac {1} {2 v_ {\ infty}}\ ліворуч (-\ ln\ ліворуч (\ frac {v (t) +v_ {\ infty}} {v_ {\ intty}}\ праворуч) +\ ln\ ліворуч (\ frac {v_ {\ infty} -v (t)} {v_ {\ intty}}\ праворуч) =-\ frac {\ бета} {m} t
\ end {масив}\ nonumber\]

Після деяких алгебраїчних маніпуляцій рівняння (8.6.114) можна переписати як

$$\ln \left(\frac{v_{\infty}-v(t)}{v(t)+v_{\infty}}\right)=-\frac{2 v_{\infty} \beta}{m} t \nonumber$$

Рівняння експоненції (8.6.115) дає

$$\left(\frac{v_{\infty}-v(t)}{v(t)+v_{\infty}}\right)=e^{-\frac{2 v_{\omega} \beta}{m} t} \nonumber$$

Після деякої алгебраїчної перестановки y -складова швидкості як функція часу задається

\ [\ почати {масив} {c}
v (t) =v_ {\ infty}\ ліворуч (\ frac {1-e^ {-\ frac {2 v_ {w}\ beta_ {t}} {m}}} {1+e^ {-\ frac {2 v_ {\ infty}\ beta_ {t}} {m}}}}\ праворуч) =v_ _ {\ infty}\ tan h\ ліворуч (\ frac {v_ {\ infty}\ бета} {м} т\ справа)\\ текст {де}
\ frac {v_ {\ infty}\ бета} {m} =\ frac {\ бета} {m}\ sqrt {\ frac {m g} {\ бета}} =\ sqrt {\ frac {\ бета г} {m}} =\ sqrt {\ frac {(1/2) C_ {D} A\ rho g} {m}}
\ end {масив}\ nonumber\]