2.12: Рівняння Шредінгера та колапс хвильової функції

Ми бачили, що хвильова функція вільної частинки маси\(m\) задовольняє,\[\label{e2.78} \psi(x,t)=\int_{-\infty}^{\infty}\bar{\psi}(k)\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\,dk,\] де\(\bar{\psi}(k)\) визначається\(\psi(x,0)\), і\[\label{e2.79} \omega(k) = \frac{\hbar\,k^{\,2}}{2\,m}.\] Випливає з Рівняння ([e2.78]), що\[\label{e2.80} \frac{\partial\psi}{\partial x} = \int_{-\infty}^{\infty}({\rm i}\,k)\,\bar{\psi}(k)\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\,dk,\] і\[\frac{\partial^{\,2}\psi}{\partial x^{\,2}} = \int_{-\infty}^{\infty}(-k^{\,2})\,\bar{\psi}(k)\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\,dk,\] тоді як\[\frac{\partial \psi}{\partial t} = \int_{-\infty}^{\infty}(-{\rm i}\,\omega)\,\bar{\psi}(k)\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\,dk.\] Таким чином,\[{\rm i}\,\frac{\partial\psi}{\partial t} +\frac{\hbar}{2\,m}\,\frac{\partial^{\,2}\psi}{\partial x^{\,2}} = \int_{-\infty}^{\infty}\left(\omega-\frac{\hbar\,k^{\,2}}{2\,m}\right)\bar{\psi}(k)\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\,dk= 0,\] де було використано дисперсійне відношення ([e2.79]). Помноживши на\(\hbar\), отримуємо\[\label{e2.84} {\rm i}\,\hbar\,\frac{\partial\psi}{\partial t} = -\frac{\hbar^{\,2}}{2\,m}\frac{\partial^{\,2}\psi}{\partial x^{\,2}}.\] Цей вираз відомий як рівняння Шредінгера, оскільки воно було вперше введено Ервіном Шредінгером в 1926 році. Рівняння Шредінгера - це лінійне рівняння з частинними похідними другого порядку, яке регулює часову еволюцію хвильової функції частинки і, як правило, легше розв'язати, ніж інтегральне рівняння ([e2.78]).

Звичайно, Equation ([e2.84]) застосовується лише до вільно рухаються частинок. На щастя, досить легко здогадатися узагальнення цього рівняння для частинок, що рухаються в якомусь потенціалі\(V(x)\). Імовірно, з Equation ([e2.80]), що ми можемо ідентифікувати за\(k\) допомогою диференціального оператора\(-{\rm i}\,\partial/\partial x\). Отже, диференціальний оператор праворуч рівняння ([e2.84]) еквівалентний\(\hbar^{\,2}\,k^{\,2}/(2\,m)\). Але,\(p = \hbar\,k\). Таким чином, оператор також еквівалентний\(p^{\,2}/(2\,m)\), який є всього лише енергією вільно рухається частинки. Однак при наявності потенціалу\(V(x)\) записується енергія частинки\(p^{\,2}/(2\,m) + V\). Таким чином, здається розумним зробити підстановку\[-\frac{\hbar^{\,2}}{2\,m}\frac{\partial^{\,2}}{\partial x^{\,2}}\rightarrow -\frac{\hbar^{\,2}}{2\,m}\frac{\partial^{\,2}}{\partial x^{\,2}} + V(x).\] Це призводить до загальної (одновимірної) форми рівняння Шредінгера:\[{\rm i}\,\hbar\,\frac{\partial\psi}{\partial t} = -\frac{\hbar^{\,2}}{2\,m}\frac{\partial^{\,2}\psi}{\partial x^{\,2}} + V(x)\,\psi.\]

Згортання хвильової функції

Розглянемо розширену хвильову функцію,\(\psi(x,t)\). Відповідно до нашої звичайної інтерпретації,\(|\psi(x,t)|^{\,2}\) пропорційна щільності ймовірності вимірювання положення частинки, що дає значення\(x\) в часі\(t\). Якщо хвильова функція розширена, то існує широкий діапазон ймовірних значень, які це вимірювання може дати. Припустимо, що робимо такий вимір, і отримуємо значення\(x_0\). Тепер ми знаємо, що частка знаходиться за адресою\(x=x_0\). Якщо ми зробимо ще одне вимірювання відразу після першого, то здоровий глузд говорить нам, що ми повинні отримати те саме значення\(x_0\), оскільки частинка не може помітно змістити положення в нескінченно малому часовому інтервалі. Таким чином, відразу після першого вимірювання вимірювання положення частинки, безумовно, дасть значення\(x_0\), і не має шансів дати будь-яке інше значення. Це означає, що хвильова функція повинна була згорнутися до якоїсь функції «спайка», розташованої на\(x=x_0\). Це проілюстровано на малюнку [coll]. Звичайно, як тільки хвильова функція звалилася, вона знову починає розширюватися, як обговорювалося в розділі 1.13. Таким чином, друге вимірювання повинно бути зроблено досить швидко після першого, щоб гарантувати, що буде отриманий той же результат.

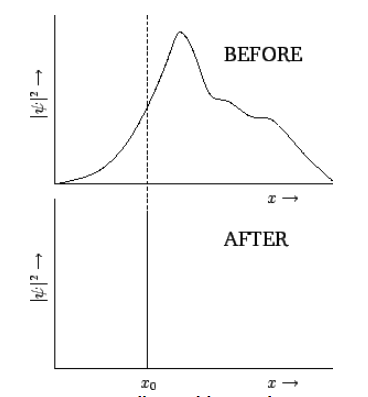
Малюнок 9: Згортання хвильової функції при вимірюванні.

Попереднє обговорення ілюструє важливий момент квантової механіки. А саме, що хвильова функція частинки змінюється розривно (у часі) кожного разу, коли проводиться вимірювання. Зроблено висновок, що існує два типи часової еволюції хвильової функції в квантовій механіці. По-перше, існує плавна еволюція, яка регулюється рівнянням Шредінгера. Ця еволюція відбувається між вимірами. По-друге, існує переривчаста еволюція, яка відбувається кожного разу, коли проводиться вимірювання.

Автори та атрибуція

• Template:ContribFitzpatrick