2.11: Еволюція хвильових пакетів
- Page ID
- 77123
Ми бачили в Equation ([e2.45]), як записати хвильову функцію частинки, яка спочатку локалізована в\(x\) -просторі. Розберемо, як ця хвильова функція розвивається в часі. Відповідно до Рівняння ([e2.42]), ми маємо\[\label{e2.56} \psi(x,t) = \int_{-\infty}^{\infty} \bar{\psi}(k)\,{\rm e}^{\,{\rm i}\,\phi(k)}\,dk,\] де\[\phi(k) = k\,x - \omega(k)\,t.\] Функція\(\bar{\psi}(k)\) отримується шляхом перетворення Фур'є хвильової функції в\(t=0\). [Див. Рівняння ([e2.42a]) і ([e2.51]).] Згідно з рівнянням ([e2.53]),\(|\bar{\psi}(k)|\) сильно досягається пік навколо\(k=k_0\). Таким чином, це розумне наближення до Тейлора розширити\(\phi(k)\)\(k_0\). Зберігаючи терміни до другого порядку в\(k-k_0\), отримуємо\[\psi(x,t)\propto \int_{-\infty}^{\infty} \bar{\psi}(k)\, \exp\!\left[\,{\rm i}\left\{\phi_0+ \phi_0'\,(k-k_0) + \frac{1}{2}\,\phi_0''\,(k-k_0)^{\,2}\right\}\right],\] де\[\begin{aligned} \phi_0 &= \phi(k_0) = k_0\,x-\omega_0\,t,\\[0.5ex] \phi_0'&= \frac{d\phi(k_0)}{dk} = x - v_g\,t,\\[0.5ex] \phi_0''&=\frac{d^{\,2}\phi(k_0)}{dk^{\,2}} = - \alpha\,t,\end{aligned}\] з\[\begin{aligned} \omega_0 &= \omega(k_0),\\[0.5ex] v_g &= \frac{d\omega(k_0)}{dk},\\[0.5ex] \alpha &= \frac{d^{\,2}\omega(k_0)}{dk^{\,2}}.\label{e2.64}\end{aligned}\] підстановкою з рівняння ([e2.51]), переставляючи, а потім змінюючи змінну інтеграції на\(y=(k-k_0)/(2\,{\mit\Delta}k)\), отримуємо\[\psi(x,t)\propto {\rm e}^{\,{\rm i}\,(k_0\,x-\omega_0\,t)} \int_{-\infty}^{\infty}{\rm e}^{\, {\rm i}\,\beta_1\,y-(1+{\rm i}\,\beta_2)\,y^{\,2}}\,dy,\] де,\[\begin{aligned} \beta_1 &= 2\,{\mit\Delta}k\,(x-x_0-v_g\,t),\\[0.5ex] \beta_2&= 2\,\alpha\,({\mit\Delta}k)^{\,2}\,t.\end{aligned}\] до речі\({\mit\Delta k}=1/(2\,{\mit\Delta}x)\), де \({\mit\Delta}x\)початкова ширина хвильового пакета. Попередній вираз можна переставити, щоб дати\[\label{e2.69} \psi(x,t)\propto {\rm e}^{\,{\rm i}\,(k_0\,x-\omega_0\,t)-(1+{\rm i}\,\beta_2)\,\beta^{\,2}/4}\int_{-\infty}^\infty {\rm e}^{-(1+{\rm i}\,\beta_2)\,(y-y_0)^{\,2}}\,dy,\] де\(y_0={\rm i}\,\beta/2\) і\(\beta=\beta_1/(1+{\rm i}\,\beta_2)\). Знову змінюючи змінну інтеграції\(z=(1+{\rm i}\,\beta_2)^{1/2}\,(y-y_0)\), ми\[\psi(x,t)\propto (1+{\rm i}\,\beta_2)^{-1/2}\,{\rm e}^{\,{\rm i}\,(k_0\,x-\omega_0\,t)-(1+{\rm i}\,\beta_2)\,\beta^{\,2}/4}\int_{-\infty}^\infty {\rm e}^{-z^{\,2}}\,dz.\] отримуємо інтеграл тепер просто зводиться до числа. Отже, ми отримуємо\[\label{exxx} \psi(x,t)\propto\frac{\exp\left[\,{\rm i}\,(k_0\,x-\omega_0\,t) - (x-x_0-v_g\,t)^{\,2}\,\{1-{\rm i}\,2\,\alpha\,({\mit\Delta}k)^{\,2}\,t\}/(4\,\sigma^{\,2})\right]}{\left[1+{\rm i}\,2\,\alpha\,({\mit\Delta}k)^{\,2}\,t\right]^{1/2}},\] де\[\label{e2.70} \sigma^{\,2}(t) = ({\mit\Delta}x)^{\,2} + \frac{\alpha^{\,2}\,t^{\,2}}{4\,({\mit\Delta}x)^{\,2}}.\] Зверніть увагу, що попередня хвильова функція ідентична нашій вихідній хвильовій функції ([e2.45]) at\(t=0\). Це виправдовує наближення, яке ми зробили раніше Тейлором, розширюючи фазовий фактор\(\phi(k)\) про\(k=k_0\).
Відповідно до Рівняння ([exxx]) пишеться щільність ймовірності нашої частинки як функція часу\[|\psi(x,t)|^{\,2} \propto \sigma^{\,-1}(t)\exp\left[-\frac{(x-x_0-v_g\,t)^{\,2}}{2\,\sigma^{\,2}(t)}\right].\] Отже, розподіл ймовірностей є гауссовим, характерної ширини\(\sigma(t)\), що піки при\(x=x_0+v_g\,t\). Найбільш вірогідне положення нашої частки збігається з піком функції розподілу. Таким чином, найбільш імовірне положення частки задається\[x = x_0+v_g\,t.\] Це видно, що частка ефективно рухається з рівномірною швидкістю,\[v_g = \frac{d\omega}{dk},\] яка відома як групова швидкість. Іншими словами, плоска хвиля рухається з фазовою швидкістю\(v_p=\omega/k\), тоді як хвильовий пакет рухається з груповою швидкістю,\(v_g=d\omega/dt\). З співвідношення дисперсії ([e2.38]) для хвиль частинок випливає, що\[v_g = \frac{p}{m}.\] Однак з Рівняння ([e2.31]) видно, що це ідентично класичній швидкості частинок. Отже, співвідношення дисперсії ([e2.38]) виявляється узгодженим з класичною фізикою, зрештою, як тільки ми розуміємо, що окремі частинки повинні бути ідентифіковані за допомогою хвильових пакетів, а не плоских хвиль. Насправді плоска хвиля зазвичай інтерпретується як безперервний потік частинок, що поширюються в тому ж напрямку, що і хвиля.
Відповідно до Equation ([e2.70]), ширина нашого хвильового пакету зростає з часом. Дійсно, з Рівняння ([e2.38]) і ([e2.64]) випливає, що характерний час для хвильового пакету початкової ширини\({\mit\Delta} x\), що подвоюється в просторовій мірі, є\[t_2 \sim \frac{m\,({\mit\Delta}x)^{\,2}}{\hbar}.\] Наприклад, якщо електрон спочатку локалізований в області атомного масштабу (тобто, \({\mit\Delta} x\sim 10^{-10}\,{\rm m}\)) то час подвоєння - це лише близько\(10^{-16}\,{\rm s}\). Очевидно, що хвильові пакети частинок (для вільно рухаються частинок) поширюються дуже швидко.
Зверніть увагу, з попереднього аналізу, що швидкість поширення хвильового пакету в кінцевому рахунку регулюється другою\(\omega(k)\) похідною щодо\(k\). [Див. Рівняння ([e2.64]) і ([e2.70]).] Це пояснює, чому функціональний зв'язок між\(\omega\) і\(k\), як правило, відомий як відношення дисперсії - він регулює, наскільки швидко хвильові пакети розходяться з плином часу. Однак для особливого випадку, де\(\omega\) є лінійна функція\(k\), друга похідна по відношенню до\(k\) дорівнює нулю, а, отже, відсутня дисперсія хвильових пакетів: тобто хвильові пакети поширюються без зміни форми.\(\omega\) Співвідношення дисперсії ([e2.7]) для світлових хвиль є лінійним в\(k\). Звідси випливає, що світлові імпульси поширюються через вакуум, не поширюючись. Ще одна властивість лінійних дисперсійних відносин полягає в тому\(v_p=\omega/k\), що фаза-швидкість, і групова швидкість\(v_g=d\omega/dk\), ідентичні. Таким чином, плоскі світлові хвилі і світлові імпульси поширюються через вакуум з характерною швидкістю\(c=3\times 10^8\,{\rm m/s}\). Звичайно, співвідношення дисперсії ([e2.38]) для хвиль частинок не є лінійним\(k\). Отже, плоскі хвилі частинок та хвильові пакети частинок поширюються з різними швидкостями, а хвильові пакети частинок також поступово розсіюються з плином часу.
Принцип невизначеності Гейзенберга
Згідно з аналізом, що міститься в попередніх двох розділах, хвильовий пакет частинок, який спочатку локалізується в\(x\) -просторі з характерною шириною\({\mit\Delta}x\), також локалізується в\(k\) -просторі з характерною шириною\({\mit\Delta}k= 1/(2\,{\mit\Delta} x)\). Однак з плином часу ширина хвильового пакету в\(x\) -просторі збільшується, тоді як ширина хвильового пакету в\(k\) -просторі залишається незмінною. [Зрештою, наш попередній аналіз отриманий\(\psi(x,t)\) з Equation ([e2.56]), але припускав, що це\(\bar{\psi}(k)\) було дано рівнянням ([e2.51]) у всі часи.] Отже, загалом можна сказати, що\ begin {рівняння}\ Delta x\ Delta k\ gtrsim\ frac {1} {2}\ end {рівняння} Крім того, ми можемо думати\({\mit\Delta}x\) і\({\mit\Delta} k\) як характеризує нашу невизначеність щодо значень положення частинки та хвильового числа відповідно.
Вимірювання хвильового числа частинки\(k\), еквівалентно вимірюванню її імпульсу\(p\), тому що\(p=\hbar \,k\). Отже,\(k\) невизначеність у порядку\({\mit\Delta} k\) означає\(p\) невизначеність у порядку\({\mit\Delta}p=\hbar\,{\mit\Delta}k\). З попередньої нерівності випливає, що\ begin {рівняння}\ Delta x\ Delta p\ gtrsim\ frac {\ hbar} {2}\ end {рівняння} Це відомий принцип невизначеності Гейзенберга, вперше запропонований Вернером Гейзенбергом в 1927 році. За цим принципом неможливо одночасно виміряти положення і імпульс частинки (точно). Дійсно, гарне знання положення частинки передбачає погане знання її імпульсу, і навпаки. Зверніть увагу, що принцип невизначеності є прямим наслідком представлення частинок у вигляді хвиль.
З Рівнянь ([e2.38]), ([e2.64]) і ([e2.70]) видно, що в цілому хвильова функція частинок початкової ширини\({\mit\Delta} x\) (at\(t=0\)) поширюється\[\label{espread} \sigma\sim \frac{\hbar\,t}{m\,{\mit\Delta}x}.\] так\(t\), що її просторова протяжність стає Легко продемонструвати, що це поширення є наслідком принципу невизначеності. Оскільки початкова невизначеність у положенні частинки є\({\mit\Delta}x\), випливає, що невизначеність у її імпульсі є порядковою\(\hbar/{\mit\Delta}x\). Це означає невизначеність у швидкості\({\mit\Delta}v = \hbar/(m\,{\mit\Delta}x)\). Таким чином, якщо ми уявляємо, що частини хвильової функції поширюються на\(v_0+ {\mit\Delta}v/2\)\(v_0-{\mit\Delta}v/2\), а інші при, де середня швидкість поширення, то\(v_0\) хвильова функція буде поширюватися з часом. Дійсно\(t\), загалом ми очікуємо,\[\sigma \sim {\mit\Delta}v\,t \sim \frac{\hbar\,t}{m\,{\mit\Delta}x},\] що ширина хвильової функції буде ідентичною рівнянню ([espread]). Очевидно, що поширення хвильової функції частинки слід інтерпретувати як збільшення нашої невизначеності щодо положення частинки, а не збільшення просторової протяжності самої частинки.
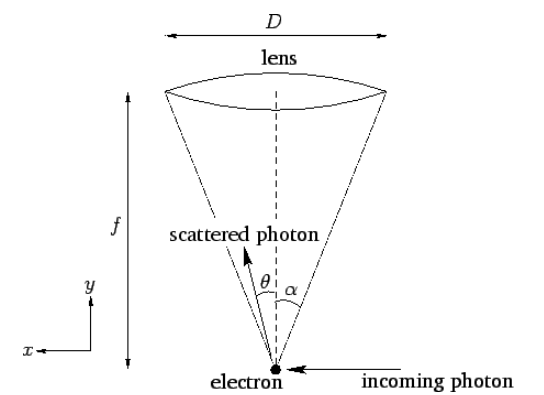
Малюнок 8: Мікроскоп Гейзенберга.
Рисунок [fh] ілюструє відомий експеримент думки, відомий як мікроскоп Гейзенберга. Припустимо, що ми намагаємося зобразити електрон за допомогою простої оптичної системи, в якій об'єктив має діаметр\(D\) і фокусну довжину\(f\). (На практиці це було б можливо лише за допомогою надзвичайно короткохвильового світла.) Відомим результатом в оптиці є те, що така система має мінімальну кутову роздільну здатність\(\lambda/D\), де\(\lambda\) знаходиться довжина хвилі світла, що висвітлює електрон. Якщо електрон розміщений у фокусі лінзи, де досягається мінімальна роздільна здатність, то це призводить до невизначеності в поперечному положенні електрона\[{\mit\Delta}x \simeq f\,\frac{\lambda}{D}.\] Однак,\[\tan\alpha = \frac{D/2}{f},\] де\(\alpha\) знаходиться напівкут, поглиблений лінзою на електроні. Припускаючи, що\(\alpha\) це мало, ми можемо написати\[\alpha\simeq \frac{D}{2\,f},\] так\[{\mit\Delta} x\simeq \frac{\lambda}{2\,\alpha}.\]. З цього випливає, що ми можемо зменшити невизначеність в положенні електрона, мінімізуючи співвідношення\(\lambda/\alpha\): тобто використовуючи короткохвильове випромінювання та ширококутну лінзу.
Розглянемо тепер мікроскоп Гейзенберга з квантово-механічної точки зору. Згідно з квантовою механікою, електрон знімається, коли він розсіює вхідний фотон до об'єктива об'єктиву. Нехай хвильовий вектор вхідного фотона має\((x,y)\) складові\((k,0)\). Див. Рисунок [fh]. Якщо розсіяний фотон піддає кут\(\theta\) з центральною лінією оптичної системи, як показано на малюнку, то записується його хвильовий вектор\((k\,\sin\theta, k\cos\theta)\). Тут ми ігноруємо будь-який зсув довжини хвилі фотона при розсіюванні - іншими словами, величина\({\bf k}\) -вектора вважається однаковою до і після розсіювання. Таким чином, зміна\(x\) -складової хвильового вектора фотона є\({\mit\Delta}k_x= k\,(\sin\theta-1)\). Це означає зміну фотонної\(x\) -складової імпульсу\({\mit\Delta}p_x = \hbar\,k\,(\sin\theta-1)\). При збереженні імпульсу\(x\) імпульс електрона зміниться на рівну і протилежну величину. Однак\(\theta\) може варіюватися весь шлях від\(-\alpha\) до\(+\alpha\), і розсіяний фотон все одно буде збиратися системою візуалізації. Звідси випливає, що невизначеність в імпульсі електрона\[{\mit\Delta} p \simeq 2\,\hbar\,k\,\sin\alpha\simeq \frac{4\pi\,\hbar\,\alpha}{\lambda}.\] Зауважте, що для зменшення невизначеності в імпульсі нам потрібно максимізувати співвідношення\(\lambda/\alpha\). Це прямо протилежне тому, що нам потрібно зробити, щоб зменшити невизначеність у позиції. Помноживши попередні два рівняння, отримаємо\[{\mit\Delta x}\,{\mit\Delta} p\sim h,\] яке по суті є принципом невизначеності.
Згідно з мікроскопом Гейзенберга, принцип невизначеності випливає з двох фактів. По-перше, неможливо виміряти будь-яку властивість мікроскопічної динамічної системи, не порушивши кілька систему. По-друге, частинки та світла енергія та імпульс квантуються. Отже, існує межа того, наскільки малими ми можемо зробити вищезгадане порушення. Таким чином, існує незменшена невизначеність в певних вимірах, яка є наслідком самого акту вимірювання.