13.10: Трансформатор

Last updated
Save as PDF

Page ID: 78646

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Ми познайомилися з трансформатором коротко в розділі 10.9. Там ми вказували, що ЕРС, індукована у вторинній котушці, дорівнює кількості витків у вторинній котушці, що перевищує швидкість зміни магнітного потоку; а потік пропорційний ЕРС, застосованої до первинного часу кількості витків у первинному. Звідси ми вивели добре відоме відношення

\[\tag{13.10.1}\dfrac{V_2}{V_1}=\dfrac{N_2}{N_1}\]

відношення первинного і вторинного напруги до кількості витків в кожному. Тепер розглянемо трансформатор більш детально, зокрема, розглянемо, що відбувається, коли ми підключаємо вторинну котушку в ланцюг і беремо з неї харчування.

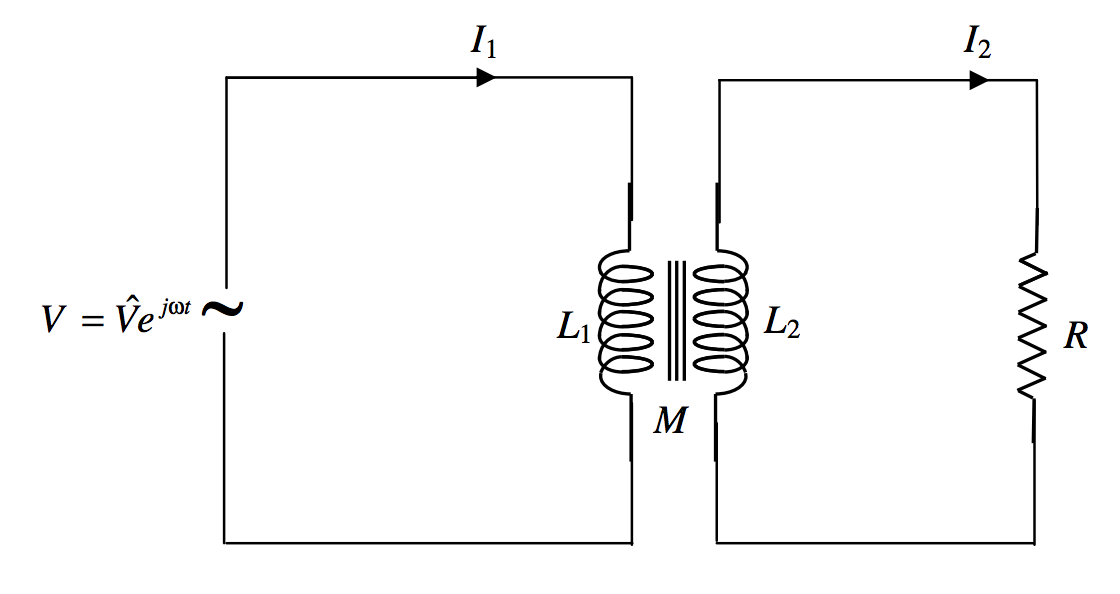
Малюнок\(\text{XIII.12}\)

На малюнку\(\text{XIII.12}\), we apply an AC EMF \(V=\hat{V}e^{j\omega t}\) to the primary circuit. The self inductance of the primary coil is \(L_1\), і в первинному ланцюзі\(I_1\) протікає змінний струм. Самоіндуктивність вторинної котушки є\(L_2\), а взаємна індуктивність двох котушок є\(M\). Якщо муфта між двома котушками дуже щільна, то в\(M=\sqrt{L_1L_2}\); іншому випадку вона менше цього. Я припускаю, що опір первинного контуру набагато менше, ніж реактивний опір, тому я збираюся нехтувати ним.

Вторинна котушка підключається до опору\(R\) . У вторинному ланцюзі\(I_2\) протікає змінний струм.

Давайте застосуємо закон Ома (або друге правило Кірхгофа) до кожного з двох контурів.

У первинному ланцюзі застосована ЕРС V протиставляється дві зворотні ЕРС:

\[\tag{13.10.2}V=L_1\dot I_1 +M\dot I_2.\]

Тобто

\[\tag{13.10.3}V=j\omega L_1 I_1 +j\omega MI_2.\]

Аналогічно для вторинного контуру:

\[\tag{13.10.4}0=j\omega MI_1+j\omega L_2I_2+RI_2.\]

Це два одночасних рівняння для струмів, і ми можемо (з невеликим зусиллям) вирішити їх для\(I_1\) і\(I_2\) :

\[\label{13.10.5}\tag{13.10.5}\left [ \dfrac{RL_1}{M}+j\left (\dfrac{\omega L_1L_2}{M}-\omega M \right )\right ]I_1=\left (\dfrac{L_2}{M}-j\dfrac{R}{\omega M}\right )V\]

\[\tag{13.10.6}\left [R+j\left ( \omega L_2-\dfrac{\omega M^2}{L_1}\right ) \right ]I_2=-\dfrac{MV}{L_1}.\]

Це було б легше зрозуміти, якби ми зробили необхідну алгебру, щоб записати їх у формах, а\(I_1=(a+jb)V\text{ and }I_2=(c+jd)V\). We could then easily see the phase relationships between the current and \(V\) також пікові значення струмів. Немає ніяких причин, чому ми не повинні спробувати це, але я буду трохи ледачим, перш ніж я це зроблю, і я збираюся припустити, що у нас є добре розроблений трансформатор, в якому вторинна котушка дійсно щільно намотана навколо первинної, і\(M=\sqrt{L_1L_2}\) якщо ви хочете, ви можете продовжувати з менш ефективним трансформатором, з\(M=k\sqrt{L_1L_2}\) де\(k\) коефіцієнт зчеплення менше 1, але я збираюся дотримуватися\(M=\sqrt{L_1L_2}\). У такому випадку рівняння\ ref {13.10.5} і 6 в кінцевому підсумку набувають форми

\[\tag{13.10.7}I_1=\left ( \dfrac{L_2}{L_1R}-j\dfrac{1}{L_1\omega}\right ) V = \left ( \dfrac{N_2^2}{N_1^2R}-j\dfrac{1}{L_1\omega}\right )V\]

\[\label{13.10.8}\tag{13.10.8}I_2=-\dfrac{1}{R}\sqrt{\dfrac{L_2}{L_1}}V=-\dfrac{N_2}{N_1R}V.\]

Ці рівняння скажуть нам при розгляді величини струмів та їх фази щодо\(V\) .

Тепер подивіться на схему, зображену на малюнку\(\text{XIII.13}\).

Малюнок\(\text{XIII.13}\)

На рис\(\text{XIII.13}\) we have a resistance \(R(N_1/N_2)^2\) in parallel with an inductance \(L_1\). Допуски цих двох елементів є, відповідно,\((N_2/N_1)^2/R\) і\(-j/(L_1\omega)\), тому загальний дохід є\(\dfrac{N_2^2}{N_1^2R}-j\dfrac{1}{L_1\omega}\). Таким чином, що стосується взаємозв'язку між струмом і напругою, то первинний ланцюг трансформатора точно еквівалентна схемі, намальованої на малюнку\(\text{XIII.13}\). Щоб побачити взаємозв'язок між\(I_1\) і\(V\), нам потрібно дивитися не далі, ніж малюнок\(\text{XIII.13}\).

Аналогічно, Equation\ ref {13.10.8} показує нам, що зв'язок між\(I_2\) і точно\(V\) такий, як якщо б у нас був генератор змінного струму ЕРС\(N_2V/N_1\) connected across \(R\), як на малюнку\(\text{XIII.14}\).

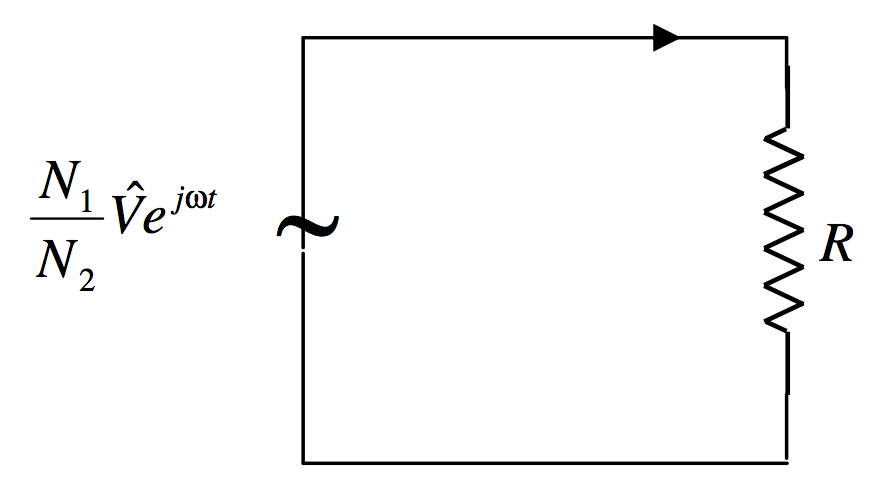
Малюнок\(\text{XIII.14}\)

Зверніть увагу, що при короткому замиканні вторинної (тобто якщо\(R = 0\) і якщо опір вторинної котушки буквально дорівнює нулю) як первинний, так і вторинний струм стають нескінченними. Якщо вторинну ланцюг залишити розімкнутою (тобто\(R = \infty\)), вторинний струм дорівнює нулю (як очікувалося), а первинний струм, також як очікувалося, не дорівнює нулю, а є\(-jV/(L_1\omega)\); That is to say, the current is of magnitude \(V/(L_1\omega)\) і він відстає від напруги на 90 ^о, так само, як ніби вторинної ланцюга там не було.