Skip to main content
LibreTexts - Ukrayinska

5.7: Трансформація Дельта-Зірка

  1. Last updated
  2. Save as PDF
  • Page ID
    78533

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Як ми зробили з резисторами в розділі 4.12, ми можемо зробити перетворення дельта-зірки за допомогою конденсаторів.

    \(\text{FIGURE V.7}\)

    Я залишаю це читачеві, щоб показати, що ємність між будь-якими двома клемами в лівій коробці така ж, як ємність між відповідними двома клемами в правій коробці за умови, що

    \[c_1=\frac{C_2C_3+C_3C_1+C_1C_2}{C_1},\label{5.7.1}\]

    \[c_2=\frac{C_2C_3+C_3C_1+C_1C_2}{C_2},\label{5.7.2}\]

    \[c_3=\frac{C_2C_3+C_3C_1+C_1C_2}{C_3},\label{5.7.3}\]

    Зворотними відносинами є

    \[C_1=\frac{c_2c_3}{c_1+c_2+c_3},\label{5.7.4}\]

    \[C_2=\frac{c_3c_1}{c_1+c_2+c_3},\label{5.7.5}\]

    \[C_3=\frac{c_1c_2}{c_1+c_2+c_3},\label{5.7.6}\]

    Наприклад, просто для задоволення, яка ємність між точками A і B на малюнку\(V.8\), на якому я позначив окремі ємності в мікрофарадах?

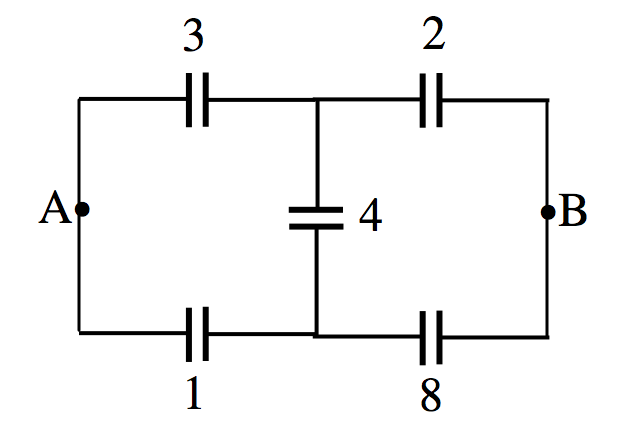
    \(\text{FIGURE V.8}\)

    Перші три конденсатора з'єднуються в дельта. Замініть їх на еквівалентну конфігурацію зірки. Після цього вона повинна бути прямолінійною. Я роблю відповідь 2.515\(\mu F\).