5.7: Потенціал

Якщо потрібна робота для переміщення маси з точки$\text{A}$ в точку$\text{B}$, кажуть, що існує гравітаційна різниця потенціалів між$\text{A}$ і$\text{B}$, з тим,$\text{B}$ що знаходиться на вищому потенціалі. Робота, необхідна для переміщення одиничної маси від$\text{A}$ до$\text{B}$, називається різницею потенціалів між$\text{A}$ і$\text{B}$. У одиницях СІ вона виражається в$\text{J kg}^{−1}$.

Ми визначили лише різницю потенціалів між двома точками. Якщо ми хочемо визначити потенціал в точці, необхідно довільно визначити потенціал в конкретній точці, щоб бути нульовим. Ми можемо, наприклад, визначити потенціал на рівні підлоги нульовим, і в цьому випадку потенціал на висоті$h$ над підлогою є$gh$; однаково ми можемо вибрати для визначення потенціалу на рівні вершини лабораторії рівним нулю, і в цьому випадку потенціал на висоті$z$ вище Верх лави є$gz$. Оскільки значення потенціалу в точці залежить від того, де ми визначаємо нуль потенціалу, часто можна побачити, що потенціал в якийсь момент дорівнює деякому математичному виразу плюс довільна константа. Значення константи буде визначено, як тільки ми вирішимо, де ми хочемо визначити нульовий потенціал.

У небесній механіці прийнято привласнювати нульовий потенціал всім точкам на нескінченній відстані від будь-яких тіл, що цікавлять.

Припустимо, ми вирішили визначити потенціал в точці,$\text{A}$ щоб бути нулем, і що потенціал в$\text{B}$ тоді$ψ$$\text{J kg}^{−1}$. Якщо ми переміщаємо точкову масу$m$ від$\text{A}$ до$\text{B}$, нам доведеться виконати кількість роботи, рівну$mψ \ \text{J}$. Потенційна енергія маси,$m$ коли вона знаходиться на$\text{B}$ - це тоді$mψ$. У цих примітках я зазвичай використовую символ$ψ$ для потенціалу в точці та символ$V$ потенційної енергії маси в точці.

При переміщенні точкової маси від$\text{A}$ до$\text{B}$, не має значення, який маршрут береться. Все, що має значення, - це різниця потенціалів між$\text{A}$ і$\text{B}$. Сили, які мають властивість, що робота, необхідна для переміщення з однієї точки в іншу, є маршрутно-незалежною, називаються консервативними силами; гравітаційні сили - консервативними. Потенціал у точці є скалярною величиною; він не має особливого напрямку, пов'язаного з ним.

Якщо це вимагає роботи для переміщення тіла з точки$\text{A}$ в точку$\text{B}$ (тобто якщо існує різниця потенціалів між$\text{A}$ і$\text{B}$, і$\text{B}$ знаходиться на більш високому потенціалі, ніж$\text{A}$), це означає, що має бути гравітаційне поле, спрямоване від$\text{B}$ до$\text{A}$.

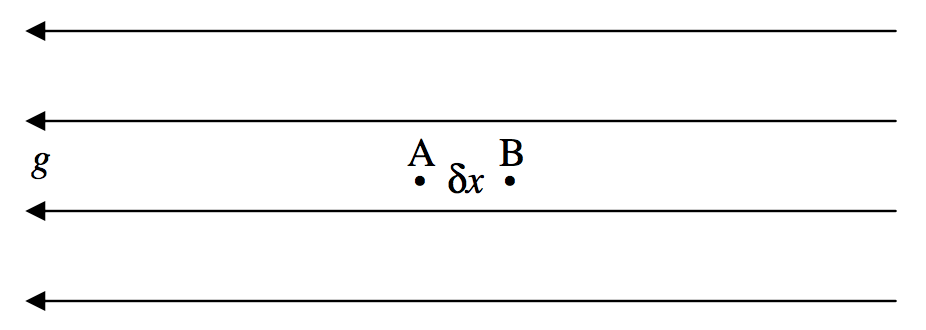
$\text{FIGURE V.22}$

$\text{V.22}$На малюнку показані дві точки$\text{B}$,$\text{A}$ і, відстань$δx$ один від одного, в області простору, де гравітаційне поле$g$ спрямоване в негативному$x$ напрямку. Ми припустимо, що різниця потенціалів між$\text{A}$ і$\text{B}$ є$δψ$. За визначенням, робота, необхідна для переміщення одиниці маси від$\text{A}$ до$\text{B}$ є$δψ$. Також за визначенням сила на одиницю маси є$g$, так що робота, виконана над одиничною масою$gδx$. Таким чином, ми маємо

$$g = - \frac{dψ}{dx}. \label{5.7.1} \tag{5.7.1}$$

Знак мінус вказує на те, що, поки потенціал збільшується зліва направо, гравітаційне поле спрямоване вліво. На словах гравітаційне поле мінус потенційний градієнт.

Це був одновимірний приклад. У більш пізньому розділі, коли ми обговорюємо векторний оператор$\nabla$, ми запишемо рівняння$\ref{5.7.1}$ в його тривимірному вигляді

$$\textbf{g} = - \textbf{grad}ψ = - \nabla ψ. \label{5.7.2} \tag{5.7.2}$$

Хоча$ψ$ сама по собі є скалярною величиною, що не має спрямованих властивостей, її градієнт - це, звичайно ж, вектор.