19.2: Обстеження зірок
- Page ID
- 78261
Цілі навчання
До кінця цього розділу ви зможете:
- Зрозумійте поняття тріангуляції відстаней до віддалених об'єктів, включаючи зірки
- Поясніть, чому космічні супутники забезпечують більш точні відстані, ніж наземні методи
- Обговоріть зусилля астрономів з вивчення найближчих до Сонця зірок
Це величезний крок, щоб перейти від планет до зірок. Наприклад, наш зонд «Вояджер 1», який був запущений в 1977 році, тепер подорожував далі від Землі, ніж будь-який інший космічний корабель. Як це написано в 2016 році, «Вояджер 1» - 134 АС від Сонця. 1 Найближча зірка, однак, - це сотні тисяч АС з Землі. Незважаючи на це, ми можемо, в принципі, оглядати відстані до зірок, використовуючи ту саму техніку, яку використовує інженер-будівельник для огляду відстані до недоступної гори чи дерева - метод тріангуляції.
Тріангуляція в космосі
Практичний приклад тріангуляції - власне глибинне сприйняття. Як вам приємно виявити щоранку, коли ви дивитеся в дзеркало, ваші два очі розташовані на деякій відстані один від одного. Тому ви розглядаєте світ з двох різних точок зору, і саме ця подвійна перспектива дозволяє отримати загальне уявлення про те, наскільки далеко знаходяться об'єкти.
Щоб побачити, що ми маємо на увазі, візьміть ручку і тримайте її на кілька дюймів перед обличчям. Подивіться на нього спочатку одним оком (закривши інше), а потім перемикайте очі. Зверніть увагу, як перо, здається, зміщується щодо предметів по всій кімнаті. Тепер тримайте ручку на відстані витягнутої руки: зрушення менше. Якщо ви пограєте з переміщенням ручки на деякий час, ви помітите, що чим далі ви її тримаєте, тим менше вона, здається, зміщується. Ваш мозок автоматично виконує такі порівняння і дає вам досить гарне відчуття того, наскільки далеко знаходяться речі у вашому безпосередньому сусідстві.
Якби руки були зроблені з гуми, ви могли б розтягнути ручку досить далеко від очей, щоб зрушення стало непомітним. Це тому, що наше сприйняття глибини не вдається для об'єктів, що знаходяться на відстані кількох десятків метрів. Для того, щоб побачити зсув об'єкта міського кварталу або більше від вас, ваші очі потрібно було б розвести набагато далі.
Давайте подивимося, як геодезисти користуються однією і тією ж ідеєю. Припустимо, ви намагаєтеся виміряти відстань до дерева через глибоку річку (рис.\(\PageIndex{1}\)). Ви встановили дві станції спостереження на деякій відстані один від одного. Ця відстань (лінія AB на малюнку\(\PageIndex{1}\)) називається базовою лінією. Тепер напрямок до дерева (С на малюнку) по відношенню до базової лінії спостерігається від кожної станції. Зверніть увагу, що C з'являється в різних напрямках від двох станцій. Ця видима зміна напрямку віддаленого об'єкта внаслідок зміни точки огляду спостерігача називається паралаксом.
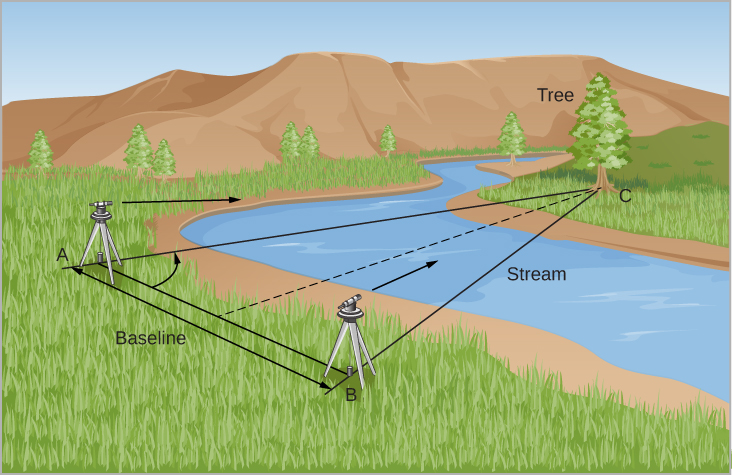
Паралакс - це також кут, який роблять лінії змінного струму та BC - у математичному плані кут, підведений базовою лінією. Знання кутів у A та B та довжини базової лінії, AB, дозволяє вирішити трикутник ABC для будь-якого його виміру - скажімо, відстані змінного струму або BC. Рішення може бути досягнуто шляхом побудови масштабного креслення або за допомогою тригонометрії для числового розрахунку. Якби дерево було далі, весь трикутник був би довшим і стрункішим, а кут паралакса був би меншим. Таким чином, у нас є загальне правило, що чим менше паралакс, тим віддаленішим повинен бути об'єкт, який ми вимірюємо.
На практиці види базових показників, які геодезисти використовують для вимірювання відстаней на Землі, абсолютно марні, коли ми намагаємося виміряти відстані в космосі. Чим далі знаходиться астрономічний об'єкт, тим довшою має бути базова лінія, щоб дати нам розумний шанс зробити вимірювання. На жаль, майже всі астрономічні об'єкти знаходяться дуже далеко. Для вимірювання їх відстаней потрібна дуже велика базова лінія і високоточні кутові вимірювання. Місяць - єдиний об'єкт, досить близький, щоб його відстань можна було знайти досить точно за допомогою вимірювань, проведених без телескопа. Птолемей визначив відстань до Місяця правильно з точністю до декількох відсотків. Він використовував саму поворотну Землю як базову лінію, вимірюючи положення Місяця щодо зірок в два різні пори ночі.
За допомогою телескопів пізніше астрономи змогли виміряти відстані до найближчих планет і астероїдів, використовуючи діаметр Землі як базову лінію. Саме так вперше був створений АС. Однак для досягнення зірок потрібна набагато довша базова лінія для тріангуляції та надзвичайно чутливих вимірювань. Такий базовий рівень забезпечується щорічною поїздкою Землі навколо Сонця.
Відстані до зірок
Коли Земля рухається з одного боку своєї орбіти на іншу, вона люб'язно забезпечує нам базову лінію 2 AU, або близько 300 мільйонів кілометрів. Хоча це набагато більша базова лінія, ніж діаметр Землі, зірки знаходяться настільки далеко, що результуючий зсув паралакса все ще не видно неозброєним оком - навіть для найближчих зірок.
У розділі «Спостереження за небом: Народження астрономії» ми обговорювали, як ця дилема здивувала древніх греків, деякі з яких насправді припустили, що Сонце може бути центром Сонячної системи, а Земля рухається навколо неї. Аристотель та інші стверджували, однак, що Земля не може обертатися навколо Сонця. Якби це було, за їхніми словами, ми б напевно спостерігали паралакс найближчих зірок на тлі більш віддалених об'єктів, коли ми розглядали небо з різних частин орбіти Землі (рис.\(\PageIndex{3}\)). Тихо Браге (1546—1601) висунув той самий помилковий аргумент майже 2000 років потому, коли його ретельні вимірювання зоряних позицій неозброєним оком не виявили такого зсуву.
Ці ранні спостерігачі не усвідомлювали, наскільки справді віддалені зірки і наскільки мала зміна їхніх позицій, отже, навіть з усією орбітою Землі як базовою лінією. Проблема полягала в тому, що вони не мали інструментів для вимірювання зсувів паралакса занадто малих, щоб їх було видно людським оком. До вісімнадцятого століття, коли вже не було серйозних сумнівів в земній революції, стало зрозуміло, що зірки повинні бути вкрай віддаленими. Астрономи, оснащені телескопами, почали розробляти прилади, здатні вимірювати крихітні зрушення прилеглих зірок щодо фону більш віддалених (і, таким чином, незміщуваних) небесних об'єктів.
Це було значним технічним викликом, оскільки навіть для найближчих зірок кути паралакса зазвичай становлять лише частку секунди дуги. Нагадаємо, що одна секунда дуги (arcsec) - це кут всього 1/3600 градуса. Монета розміром з квартал США мала б діаметр 1 дугову секунду, якщо ви переглядали її з відстані близько 5 кілометрів (3 милі). Подумайте про те, наскільки маленький кут, що є. Недарма астрономам знадобилося багато часу, перш ніж вони змогли виміряти такі крихітні зрушення.
Перші успішні виявлення зоряного паралакса були в 1838 році, коли Фрідріх Бессель в Німеччині (рис.\(\PageIndex{2}\)), Томас Хендерсон, шотландський астроном, що працює на мисі Доброї Надії, і Фрідріх Струве в Росії самостійно вимірювали паралакси зірок 61 Цигні, Альфа Центавра, і Vega відповідно. Навіть найближча зірка, Альфа Центавра, протягом року показала сумарне зміщення всього близько 1,5 кутових секунд.

\(\PageIndex{3}\)На малюнку показано, як працюють такі виміри. Поглянута з протилежних сторін орбіти Землі, сусідня зірка зміщує положення порівняно з моделлю більш віддалених зірок. Астрономи насправді визначають паралакс як половину кута, який зірка зміщується, коли видно з протилежних сторін орбіти Землі (кут, позначений P на малюнку\(\PageIndex{3}\)). Причиною цього визначення є якраз те, що вони вважають за краще мати справу з базовою лінією 1 АС замість 2 АС.
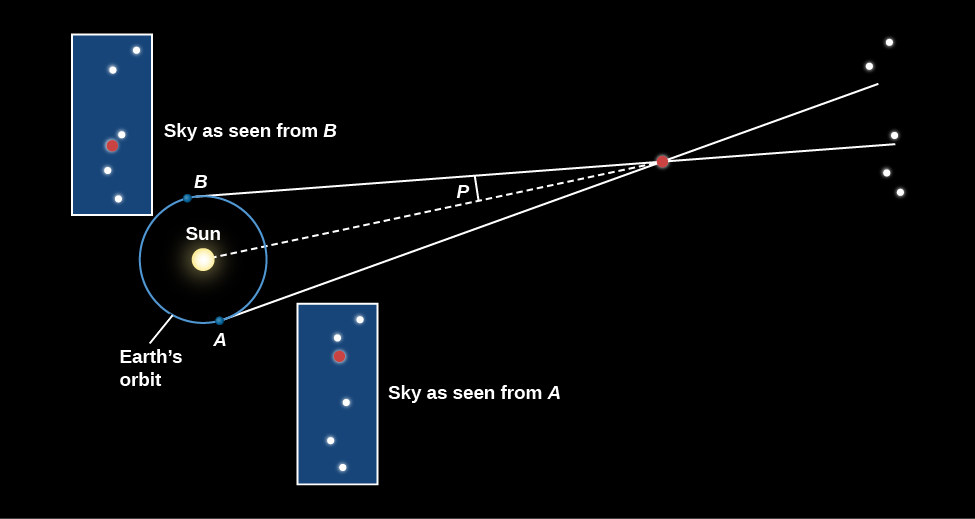
Одиниці зоряної відстані
З базовою лінією одного АС, наскільки далеко повинна бути зірка, щоб мати паралакс 1 дугову секунду? Відповідь виходить 206 265 а.о., або 3,26 світлових року. Це дорівнює 3,1 × 10 13 кілометрів (іншими словами, 31 трильйон кілометрів). Ми даємо цій одиниці спеціальну назву, parsec (pc) —похідне від «відстані, на якій ми маємо par allax однієї секунди ond.» Відстань (\(D\)) зірки в парсеках - це лише зворотна її паралакса (p) у кутових секундах; тобто
\[D=\frac{1}{p} \nonumber\]
Таким чином, зірка з паралакс 0,1 кутова секунда буде знайдена на відстані 10 парсеків, а одна з паралакс 0,05 кутова секунда буде 20 парсеків.
Ще в ті часи, коли більшість наших відстаней прийшли від вимірювань паралакса, парсек був корисною одиницею відстані, але він не такий інтуїтивний, як світловий рік. Однією з переваг світлового року як одиниці є те, що він підкреслює той факт, що, дивлячись у космос, ми також озираємося назад у час. Світло, яке ми бачимо від зірки на відстані 100 світлових років, залишило цю зірку 100 років тому. Те, що ми вивчаємо, - це не зірка, як зараз, а скоріше, як це було в минулому. Світло, яке доходить до наших телескопів сьогодні з далеких галактик, залишив їх ще до того, як Земля навіть існувала.
У цьому тексті ми будемо використовувати світлові роки як нашу одиницю відстані, але багато астрономів все ще використовують парсеки, коли вони пишуть технічні документи або розмовляють один з одним на зустрічах. Щоб перетворити між двома одиницями відстані, просто майте на увазі: 1 парсек = 3,26 світлового року, а 1 світловий рік = 0,31 парсек.
Приклад\(\PageIndex{1}\): Як далеко знаходиться світловий рік?
Світловий рік - це відстань, яку світло проходить за 1 рік. Враховуючи, що світло рухається зі швидкістю 300 000 км/с, скільки кілометрів у світловому році?
Рішення
Раніше ми дізналися, що швидкість = відстань/час. Ми можемо переставити це рівняння так, що\(\text{distance } = \text{ velocity } \times \text{ time }\). Тепер нам потрібно визначити кількість секунд в році.
Є приблизно 365 днів в 1 році. Щоб визначити кількість секунд, ми повинні оцінити кількість секунд в 1 день.
Ми можемо змінити одиниці наступним чином (зверніть увагу, як одиниці часу скасовуються):
\[ 1 \text{ day } \times 24 \text{ hr/day } \times 60 \text{ min/hr } \times 60 \text{ s/min } = 86,400 \text{ s/day} \nonumber\]
Далі, щоб отримати кількість секунд на рік:
\[ 365 \text{ days/year } \times 86,400 \text{ s/day } = 31,536,000 \text{ s/year} \nonumber\]
Тепер ми можемо помножити швидкість світла на кількість секунд на рік, щоб отримати відстань, пройдену світлом за 1 рік:
\[ \begin{aligned} \text{distance } & = \text{ velocity } \times \text{ time} \\ & = 300,000 \text{ km/s } \times 31,536,000 \text{ s} \\ & =9.46 \times 10^{12} \text{ km} \end{aligned} \nonumber\]
Це майже 10 000 000 000 000 км, які світло охоплює за рік. Щоб допомогти вам уявити, наскільки довга ця відстань, ми згадаємо, що струна довжиною 1 світловий рік може поміститися навколо окружності Землі 236 мільйонів разів.
Вправа\(\PageIndex{1}\)
Число вище дійсно велике. Що станеться, якщо ми поставимо це в терміни, які можуть бути трохи зрозумілішими, як діаметр Землі? Діаметр Землі становить близько 12 700 км.
- Відповідь
-
\[ \begin{aligned} 1 \text{ light-year } & = 9.46 \times 10^{12} \text{ km} \\ & =9.46 \times 10^{12} \text{ km } \times \frac{1 \text{ Earth diameter}}{12,700 \text{ km}} \\ & =7.45 \times 10^8 \text{ Earth diameters} \end{aligned} \nonumber\]
Це означає, що 1 світловий рік приблизно в 745 мільйонів разів перевищує діаметр Землі.
ІМЕНУВАННЯ ЗІРОК
Можливо, вам буде цікаво, чому зірки мають такий заплутаний асортимент імен. Просто подивіться на перші три зірки, щоб виміряти їх паралакси: 61 Cygni, Альфа Центавра та Вега. Кожне з цих імен походить від іншої традиції позначення зірок.
Найяскравіші зірки мають імена, які походять від стародавніх. Деякі з грецької мови, наприклад Сіріус, що означає «випалений» - посилання на його блиск. Деякі з них з латинської мови, але багато з найвідоміших імен з арабської, тому що, як обговорювалося в Спостерігаючи за небом: Народження астрономії, значна частина грецької та римської астрономії була «знову відкрита» в Європі після темних віків за допомогою арабських перекладів. Вега, наприклад, означає «махаючий орел», а Бетельгейзе (вимовляється «Жук-сік») означає «права рука центральної».
У 1603 році німецький астроном Йоганн Байєр (1572—1625) ввів більш системний підхід до іменування зірок. Для кожного сузір'я він присвоював грецьку букву найяскравішим зіркам, приблизно в порядку яскравості. Наприклад, у сузір'ї Оріона Бетельгейзе є найяскравішою зіркою, тому вона отримала першу літеру грецького алфавіту - альфа - і відома як Альфа Оріоніс. («Оріоніс» - присвійна форма Оріона, тому Альфа Оріоніс означає «перший з Оріона».) Зірка під назвою Ригель, будучи другою найяскравішою в цьому сузір'ї, називається Beta Orionis (Рисунок\(\PageIndex{4}\)). Оскільки в грецькому алфавіті 24 літери, ця система дозволяє маркування 24 зірок у кожному сузір'ї, але сузір'я мають набагато більше зірок, ніж це.
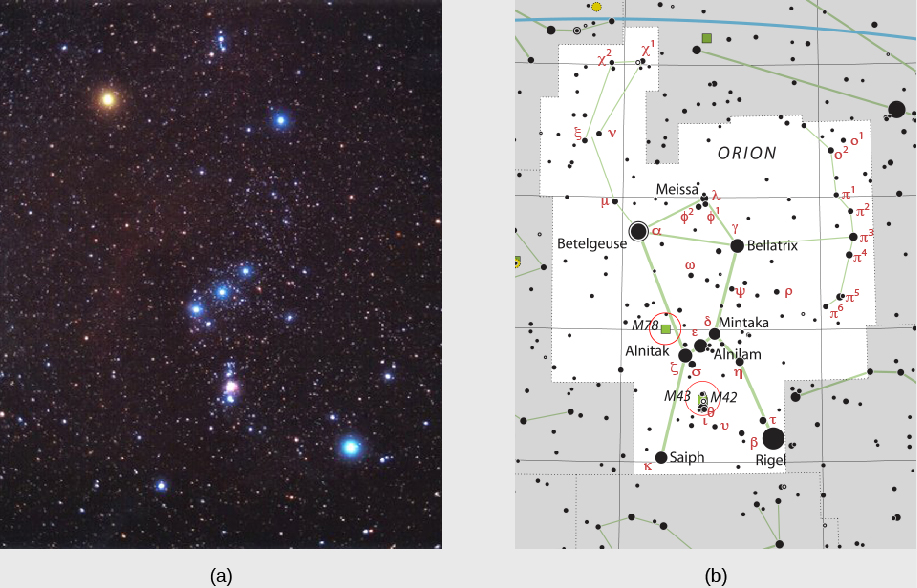
У 1725 році англійський королівський астроном Джон Фламстід ввів ще одну систему, в якій більш яскраві зірки в результаті отримали число в кожному сузір'ї в порядку їх розташування на небі або, точніше, їх правильного піднесення. (Система координат неба, що включає правильне сходження, обговорювалася на Землі, Місяці та Небі.) У цій системі Бетельгейзе називається 58 Orionis і 61 Cygni - 61-а зірка в сузір'ї Лебедя.
Стає гірше. Коли астрономи стали все більше розуміти про зірки, вони склали серію спеціалізованих зіркових каталогів, і шанувальники цих каталогів почали називати зірки за їх каталожними номерами. Якщо ви подивитеся на Додаток I - наш список найближчих зірок (багато з яких занадто слабкі, щоб отримати стародавнє ім'я, букву Байєра або число Фламстіда) - ви побачите посилання на деякі з цих каталогів. Прикладом може служити набір зірок, позначений номером BD, для «Bonner Durchmusterung». Це був каталог мамонтів з більш ніж 324 000 зірок у серії зон на небі, організований в Боннській обсерваторії в 1850-х і 1860-х роках. Майте на увазі, що цей каталог був зроблений до того, як фотографія або комп'ютери почали використовувати, тому положення кожної зірки потрібно було виміряти (принаймні двічі) на око, складна справа.
Існує також зовсім інша система відстеження зірок, світність яких змінюється, і інша для зірок, які вибухонебезпечно світлішають у непередбачувані часи. Астрономи звикли до багатьох різних систем іменування зірок, але студенти часто вважають їх здивованими і бажають, щоб астрономи оселилися на одному. Не затримуйте дихання: в астрономії, як і в багатьох сферах людської думки, традиція тримає потужну привабливість. Тим не менш, з високошвидкісними комп'ютерними базами даних, щоб допомогти людській пам'яті, імена можуть ставати все менш потрібними. Сьогоднішні астрономи часто посилаються на зірки за їх точним розташуванням на небі, а не їх іменами або різними каталожними номерами.
Найближчі зірки
Жодна відома зірка (крім Сонця) не знаходиться в межах 1 світлового року або навіть 1 парсек від Землі. Найближчими до Сонця зоряними сусідами є три зірки в сузір'ї Центавра. Для неозброєного ока найяскравіша з цих трьох зірок - Альфа Центавра, яка знаходиться всього в 30○ від південного небесного полюса і, отже, не видно з материка США. Сам Альфа Центавра є бінарною зіркою - дві зірки у взаємній революції—занадто близько один до одного, щоб їх можна було відрізнити без телескопа. Ці дві зірки знаходяться в 4,4 світлових року від нас. Поруч знаходиться третя слабка зірка, відома як Проксима Центавра. Проксима, з відстанню 4,3 світлових року, трохи ближче до нас, ніж дві інші зірки. Якщо Проксима Центавра є частиною потрійної зоряної системи з двійковим Альфа Центавра, як здається ймовірним, то її орбітальний період може бути довшим 500 000 років.
Проксима Центавра є прикладом найпоширенішого типу зірки та нашого найпоширенішого типу зоряного сусіда (як ми бачили в «Зірки: Небесна перепис»). Маломасові червоні карлики M складають близько 70% всіх зірок і домінують у переписі зірок в межах 10 парсек Сонця. Останнє обстеження сонячного сусідства нарахувало 357 зірок і коричневих карликів в межах 10 парсеків, і 248 з них - червоні карлики. Тим не менш, якби ви хотіли побачити М карлика неозброєним оком, вам не пощастило. Ці зірки виробляють лише частину світла Сонця, і майже всі вони потребують виявлення телескопа.
Найближча зірка, видима без телескопа з більшої частини Сполучених Штатів, є найяскравішою, що з'являється з усіх зірок, Сіріус, яка має відстань трохи більше 8 світлових років. Це теж двійкова система, що складається зі слабкого білого карлика, що обертається навколо блакитно-білої зірки основної послідовності. Цікавий збіг чисел, що світло доходить до нас від Сонця приблизно за 8 хвилин, а від наступної яскравої зірки на небі приблизно за 8 років.
Приклад\(\PageIndex{2}\): Розрахунок діаметра Сонця
Для сусідніх зірок ми можемо виміряти видимий зсув в їх положеннях, коли Земля обертається навколо Сонця. Ми писали раніше, що об'єкт повинен бути 206,265 AU віддалений, щоб мати паралакс однієї секунди дуги. Це повинно здатися дуже дивним числом, але ви можете розібратися, чому це правильне значення. Ми почнемо з оцінки діаметра Сонця, а потім застосуємо ту саму ідею до зірки з паралакс в 1 дугову секунду. Зробіть ескіз, який має кругле коло для зображення Сонця, розмістіть Землю на деякій відстані та поставте на неї спостерігача. Намалюйте дві лінії від точки, де стоїть спостерігач, по одній до кожної сторони Сонця. Намалюйте коло, зосереджене на Землі, з його окружністю, що проходить через центр Сонця. Тепер подумайте про пропорції. Сонце охоплює близько півградуса на небі. Повне коло має 360○. Окружність окружності, зосередженої на Землі і проходить через Сонце, задається:
\[\text{circumference } =2 \pi \times 93,000,000 \text{ miles} \nonumber\]
Потім однакові наступні два співвідношення:
\[\frac{0.5^{\circ}}{360^{\circ}} = \frac{\text{diameter of Sun}}{2 \pi \times 93,000,000} \nonumber\]
Обчисліть діаметр Сонця. Як ваша відповідь порівнюється з фактичним діаметром?
Рішення
Щоб вирішити для діаметра Сонця, ми можемо оцінити вираз вище.
\ [\ почати {вирівняний}\ текст {діаметр сонця} & =\ розрив {0.5^ {\ circ}} {360^ {\ circ}}
\ раз 2\ pi\ times 93 000,000\ текст {милі}\ =811,577\ текст {милі}\ кінець {вирівняний}\ nonumber\]
Це дуже близько до істинного значення близько 848 000 миль.
Вправа\(\PageIndex{2}\)
Тепер застосуйте цю ідею для обчислення відстані до зірки, яка має паралакс 1 arcsec. Намалюйте картинку, схожу на ту, яку ми запропонували вище, і розрахуйте відстань в АС. (Підказка: Пам'ятайте, що кут паралакса визначається 1 AU, а не 2 AU, і що 3600 кутових секунд = 1 градус.)
- Відповідь
-
206 265 ГРН.
Вимірювання паралаксів у просторі
Вимірювання зоряного паралакса були революціонізовані запуском космічного корабля «Гіппаркос» в 1989 році, який вимірював відстані для тисяч зірок приблизно до 300 світлових років з точністю від 10 до 20% (див. Рисунок\(\PageIndex{5}\) та особливість паралакса та космічної астрономії нижче). Однак навіть 300 світлових років становлять менше 1% розміру головного диска нашої Галактики.
У грудні 2013 року Європейське космічне агентство запустило наступника Гіппаркоса на ім'я Гайя. Гайя вимірює положення та відстані майже до одного мільярда зірок з точністю до декількох мільйонних часток дугової секунди. Межа відстані Гайї буде поширюватися далеко за межі Гіппаркоса, вивчаючи зірки до 30 000 світлових років (в 100 разів далі, ніж Гіппаркос, охоплюючи майже 1/3 галактичного диска). Гайя також зможе виміряти належні рухи 2 для тисяч зірок у ореолі Чумацького шляху - те, що можна зробити лише для найяскравіших зірок прямо зараз. Наприкінці місії Гайї ми не тільки матимемо тривимірну карту великої частки нашої власної Галактики Чумацького Шляху, але й матимемо сильну ланку в ланцюжку космічних відстаней, про які ми обговорюємо в цьому розділі. Проте, щоб розширити цей ланцюг за межі досяжності Гайї та дослідити відстані до довколишніх галактик, нам потрібні абсолютно нові методи.
паралакс і космічна астрономія
Однією з найскладніших речей щодо точного вимірювання крихітних кутів зсуву паралакса від Землі є те, що ви повинні спостерігати за зірками через атмосферу нашої планети. Як ми бачили в астрономічних приладах, ефект атмосфери полягає в розподілі точок зоряного світла на нечіткі диски, що ускладнює точні вимірювання їх положень. Астрономи давно мріяли про можливість вимірювати паралакси з космосу, а дві орбітальні обсерваторії тепер перетворили цю мрію в реальність.
Назва супутника Гіппаркос, запущений у 1989 році Європейським космічним агентством, є абревіатурою для високоточного супутника збору паралакс і даниною Гіппарху, новаторському грецькому астроному, роботу якого ми обговорювали в Спостерігаючи за небом: Народження астрономії. Супутник був розроблений для проведення найбільш точних вимірювань паралакса в історії, з 36000 кілометрів над Землею. Однак його бортовий ракетний двигун не вдалося запустити, що означало, що він не отримав необхідного імпульсу для досягнення бажаної висоти. Гіппаркос закінчився провівши своє 4-річне життя на еліптичній орбіті, яка варіювалася від 500 до 36 000 кілометрів у висоту. На цій орбіті супутник занурювався в радіаційні пояси Землі кожні 5 годин або близько того, що, нарешті, позначилося на сонячних батареях, які забезпечували енергію для живлення приладів.
Проте місія виявилася успішною, в результаті чого вийшло два каталоги. Один дає позиції 120 000 зірок з точністю до однієї тисячної секунди - про діаметр м'яча для гольфу в Нью-Йорку, як видно з Європи. Другий каталог містить інформацію для більш ніж мільйона зірок, положення яких були виміряні до тридцяти тисячних часток дугової секунди. Тепер ми маємо точні вимірювання паралакса зірок на відстані близько 300 світлових років. (За допомогою наземних телескопів точні вимірювання були здійснені лише приблизно до 60 світлових років.)
Для того, щоб спиратися на успіх Гіппаркоса, в 2013 році Європейське космічне агентство запустило новий супутник під назвою Gaia. Місія Gaia запланована на 5 років. Оскільки Гайя несе більші телескопи, ніж Гіппаркос, вона може спостерігати слабкі зірки та вимірювати їх положення в 200 разів точніше. Основна мета місії Gaia - зробити точну тривимірну карту цієї частини Галактики протягом приблизно 30 000 світлових років, спостерігаючи за 1 мільярдом зірок 70 разів кожна, вимірюючи їх позиції і, отже, їх паралакси, а також їх яскравість.
Тривалий час вимірювання паралаксів та точних зоряних положень було затоною астрономічних досліджень - головним чином тому, що точність вимірювань не сильно покращувалася протягом приблизно 100 років. Однак здатність проводити вимірювання з космосу зробила революцію в цій галузі астрономії і буде продовжувати забезпечувати критичну ланку в нашому ланцюжку космічних відстаней.
Європейське космічне агентство (ESA) підтримує веб-сайт місії Gaia, де ви можете дізнатись більше про місію Gaia та отримати останні новини про спостереження Gaia.
Щоб дізнатись більше про Гіппаркоса, вивчіть цю веб-сторінку Європейського космічного агентства з водкою ESA, що відображає галактику - від Гіппаркоса до Гайї.
Резюме
Для зірок, які знаходяться відносно поруч, ми можемо «тріангулювати» відстані від базової лінії, створеної щорічним рухом Землі навколо Сонця. Половина зсуву в положенні сусідньої зірки відносно дуже віддалених фонових зірок, як розглядається з протилежних сторін орбіти Землі, називається паралакс цієї зірки і є мірою її відстані. Одиницями, що використовуються для вимірювання зоряної відстані, є світловий рік, відстань світла проходить за 1 рік, і парсек (шт), відстань зірки з паралакс 1 кутова секунда (1 парсек = 3,26 світлових років). Найближча зірка, червоний карлик, знаходиться за 1 парсек. Перші успішні вимірювання зоряних паралаксів були повідомлені в 1838 році. Вимірювання паралакса є основоположною ланкою в ланцюжку космічних відстаней. Супутник Hipparcos дозволив нам вимірювати точні паралакси для зірок приблизно до 300 світлових років, а місія Gaia призведе до паралаксів до 30 000 світлових років.
Виноски
1 Щоб мати певну основу для порівняння, карликова планета Плутон обертається на середній відстані 40 а.е. від Сонця, а карликова планета Еріда в даний час приблизно 96 а.е. від Сонця.
2 Правильний рух (як обговорюється в Аналізі Starlight, - це рух зірки по небу (перпендикулярно нашій лінії зору).
Глосарій
- паралакс
- явне зміщення сусідньої зірки, що виникає в результаті руху Землі навколо Сонця
- парсек
- одиниця відстані в астрономії, що дорівнює 3,26 світлових років; на відстані 1 парсек зірка має паралакс 1 кусекунда
