Skip to main content
LibreTexts - Ukrayinska

18.1: Попередня тригонометрія

  1. Last updated
  2. Save as PDF
  • Page ID
    56342

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

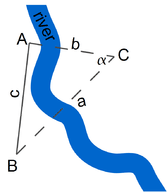
    Задача тригонометрії
    Малюнок\(\PageIndex{1}\): Основна проблема тригонометрії.

    На сторінці за адресою http://www.phy6.org/stargaze/Strig1.htm описана основна задача тригонометрії (малюнок вище): знаходження відстані до якоїсь далекої точки С, враховуючи напрямки, в яких С з'являється з двох кінців виміряної базової лінії AB. Ця проблема стає дещо простіше, якщо:

    1. Базова лінія перпендикулярна лінії від її середини до об'єкта, так що\(\Delta ABC\) симетрична. Позначимо її рівні сторони як\(AB=BC=r\).
    2. Довжина\(c\) базової лінії\(AB\) набагато менше, ніж\(r\). Це означає, що кут\(\alpha\) між\(AC\) і\(BC\) невеликий; цей кут відомий як паралакс\(C\), як видно з\(AB\).
    3. Ми не просимо великої точності, але задоволені приблизним значенням відстані — скажімо, в межах 1%.
    Задача тригонометрії 2
    Малюнок\(\PageIndex{2}\): Спрощений варіант завдання (не масштабувати).

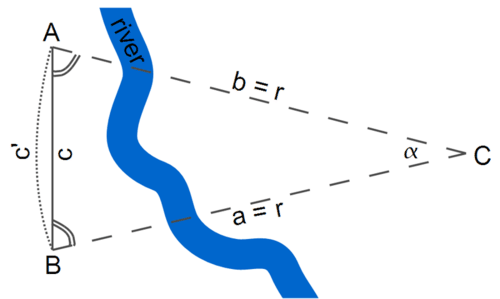
    Представлений тут метод вже використовувався стародавніми греками понад 2000 років тому. Вони знали, що довжина кола радіуса\(r\) була\(2\pi r\), де\(\pi\) (сучасне позначення, а не один з греків, хоча і\(\pi\) є частиною їх алфавіту) позначає число трохи більше 3; приблизно

    \(\pi\approx\,3.14159\ldots\)

    Примітка

    Грецький математик Архімед вивів\(\pi\) приблизно з 4-значною точністю, хоча висловив це по-різному, оскільки десяткові дроби з'явилися в Європі лише через якихось 1000 років.

    У цьому випадку (див. Рисунок вище) ми можемо наблизити\(\Delta ABC\) як «зріз» набагато більшого кола; в цьому випадку довжина базової лінії приблизно дорівнює довжині відповідної дуги:

    \[c\,\approx\,c′\]

    У колі є 360 градусів і\(\alpha\) градусів в цій конкретній дузі; оскільки 360 градусів відповідає одній окружності довжини дуги (\(2\pi r\)),\(\alpha\) градуси будуть відповідати довжині дуги

    \[c′\,=\,\frac{\alpha}{360^o}\times 2\pi r\]

    Вирішуючи для\(r\) і підключивши\(c\,\approx\,c′\), знаходимо

    \[r\,=\,\frac{360^o}{2\pi\alpha}\times c\]

    Ми вирішили для з\(r\) точки зору\(c\). Наприклад, якщо ми це знаємо\(\alpha\approx 6^o\) (ми побачимо, чому це актуально пізніше),\(2\pi\alpha\,=\,36^o\) і ми отримаємо:

    \[r\,=\,10c′\]