18.11: Принцип рівноділення

Теорема про рівноділення, також відома як закон рівноділення, рівноділення енергії або просто рівноділення, стверджує, що кожен ступінь свободи, яка з'являється лише квадратично в загальній енергії, має середню енергію\(½k_BT\) в тепловій рівновазі і\(½k_B\) сприяє тепловій системі ємність. Тут\(k_B\) знаходиться постійна Больцмана, а T - температура в Кельвіні. Закон рівноділення енергії стверджує, що кожен квадратичний член в класичному вираженні для енергії вносить ½ кБт в середню енергію. Наприклад, рух атома має три ступені свободи (кількість шляхів поглинання енергії), що відповідають компонентам x, y та z його імпульсу. Оскільки ці моменти з'являються квадратично в кінетичній енергії, кожен атом має середню кінетичну енергію\(3/2k_BT\) в тепловій рівновазі. Число ступенів свободи молекули багатоатомного газу\(N\) - це\(3N\) де число атомів в молекулі. Це дорівнює кількості координат для системи; наприклад, для двох атомів ви матимете x, y, z для кожного атома.

Переклади

Поступальний внесок в середню енергію виводиться через похідну поступального розділу:

\[ \langle E_{trans} \rangle = - \dfrac{1}{q_{trans}} \dfrac{\partial q_{trans}}{\partial \beta} \label{Eq1} \]

Впроваджуючи функцію поступального розділення, отриману раніше, Рівняння\(\ref{Eq1}\) стає

\[= - \dfrac{\Lambda^3}{V} \dfrac{\partial }{\partial \beta} \dfrac{V}{\Lambda^3} = - \dfrac{3}{\Lambda} \dfrac{\partial \Lambda}{\partial \beta} = \dfrac{3}{2} k_BT \nonumber \]

Таким чином, три поступальні ступені свободи в трьох вимірах задовольняють теоремі рівноділення з кожним поступальним ступенем забезпечення\( ½ k_BT\) енергії.

Обертання

Розглянемо функції молекулярного поділу. Середня енергія обертання до середньої енергії виводиться через похідну поступальної перегородки:

\[ \langle E_{rot} \rangle = - \dfrac{1}{q_{rot}} \dfrac{\partial q_{rot}}{\partial \beta} \label{Eq2} \]

який, коли ви вводите функцію обертального розділу, Рівняння\(\ref{Eq2}\) стає

\[ \langle E_{rot} \rangle = -\sigma \beta \tilde{B} \dfrac{1}{\sigma \tilde{B}} \dfrac{\partial}{\partial \beta} \dfrac{1}{\beta} = \dfrac{1}{\beta} = k_BT \nonumber \]

Класичним виразом для енергії обертання двоатомної молекули є

\[ E_{rot}^{(classical)}= \dfrac{1}{2} I (\omega_x^2 + \omega_y^2) \nonumber \]

де\(I\) - момент інерції і\( \omega _x\) і\( \omega _y\) - кутові швидкості в\(x\) і\(y\) напрямках. Обертання вздовж молекулярної осі (\(z\)вісь тут) не має сенсу в квантовій механіці, оскільки обертання вздовж молекулярної осі призводять до конфігурацій, які не відрізняються від початкової конфігурації. Таким чином, два обертальні ступені свободи дали значення\(kT\) з кожним обертальним ступенем забезпечення\( ½ k_BT\) енергії.

Вібрації

Розглянемо коливальні рухи. Середня коливальна енергія до середньої енергії виводиться через похідну поступальної перегородки:

\[ \langle E_{vib} \rangle = - \dfrac{1}{q_{vib}} \dfrac{\partial q_{vib}}{\partial \beta} \label{Eq3} \]

який, коли ви вводите функцію розділення для вібрації, Рівняння\(\ref{Eq3}\) стає

\[ \langle E_{vib} \rangle = \dfrac{-1}{q_{vib}} \left( -hc\tilde{\nu}\dfrac{ e^{-hc \tilde{\nu}/k_BT}}{(1-e^{-hc \tilde{\nu}/k_BT})^2 } \right) = hc\tilde{\nu} \dfrac{ e^{-hc \tilde{\nu}/k_BT}}{\left(1-e^{-hc \tilde{\nu}/k_BT}\right) } \label{18.1.7} \]

Це можна спростити, розділивши як чисельник, так і знаменник Рівняння\(\ref{18.1.7}\) на\(e^{-hc \tilde{\nu}/k_BT}\)

\[\langle E_{vib} \rangle = hc \tilde{\nu} \left( \dfrac{ 1 }{e^{hc \tilde{\nu}/k_BT} -1} \right) \label{18.1.7B} \]

Рівняння\(\ref{18.1.7B}\) застосовується при всіх температурах, але якщо\( hc \tilde{\nu}/k_BT \ll 1\) (тобто границя високої температури), то експоненціальна в знаменнику може бути розширена

\[ e^{hc \tilde{\nu}/k_BT} -1 \approx 1 + hc \tilde{\nu}/k_BT -1 = hc \tilde{\nu}/k_BT \label{expansion} \]

і рівняння\(\ref{18.1.7B}\) стає

\[ \langle E_{vib} \rangle \approx \cancel{hc \tilde{\nu}} \left( \dfrac{1}{\cancel{ hc \tilde{\nu}}/k_BT}\right) \nonumber \]

\[ \langle E_{vib} \rangle \approx k_BT \label{18.1.10} \]

з кожним коливальним ступенем забезпечення\( k_BT\) енергії (оскільки у гамільтоніані є два квадратичні члени для гармонічного осцилятора (кінетична енергія та потенційна енергія).

Порівняння рівняння\(\ref{18.1.10}\) з класичним виразом для енергії коливань

\[ E_{vib}^{(classical)} = ½ kx^2 + ½ μv_x^2 \nonumber \]

При високій температурі теорема про рівняння дійсна, але при низькій температурі розширення в рівнянні\(\ref{expansion}\) не вдається (або потрібно більше термінів). У цьому випадку зайнято лише кілька коливальних станів, і принцип рівноділення зазвичай не застосовується.

Теплоємність

Теплоємність при постійному обсязі\(C_v\), визначається як

\[ C_v = \left(\dfrac{\partial U}{\partial T} \right)_v \nonumber \]

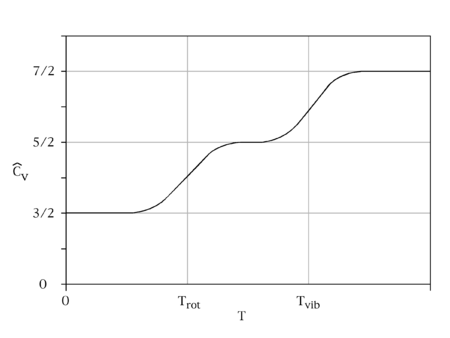
Теорема рівноділення вимагає, щоб кожен ступінь свободи, який з'являється лише квадратично в загальній енергії, мав середню енергію ½ k _B T в тепловій рівновазі і, таким чином, вносить ½kB теплової потужності системи. Таким чином, три поступальні ступені свободи кожен сприяють ½ R до (3/2 R). Внесок обертальної кінетичної енергії буде R для лінійної та 3/2R для нелінійних молекул. Для вібрації осцилятор має квадратичні кінетичні та потенційні терміни, вносячи внесок кожного коливального режиму R. Однак k _B T має бути набагато більшим, ніж відстань між рівнями квантової енергії. Якщо цього не задовольнити, то теплоємність зменшиться і яка опуститься до нуля при низьких температурах. Відповідний ступінь свободи, як кажуть, заморожений; це ситуація для вібраційних ступенів свободи при кімнатній температурі, і саме тому звичайне припущення полягає в тому, що вони не сприятимуть.

Рисунок Template:index: Ідеалізований графік молярної питомої теплоти двоатомного газу від температури. Він погоджується зі значенням (7/2) R, прогнозованим рівноділенням при високих температурах (де R - газова константа), але зменшується до (5/2) R, а потім (3/2) R при більш низьких температурах, оскільки коливальний і обертальний режими руху «заморожуються». Провал теореми про рівноділення призвів до парадоксу, який був вирішений лише квантовою механікою. Для більшості молекул перехідна температура T _гниття набагато менше кімнатної, тоді як T _vib може бути в десять разів більше або більше. Типовим прикладом є чадний газ, СО, для якого Т _гниють ≈ 2,8 К і T _vib ≈ 3103 К. Для молекул з дуже великими або слабо зв'язаними атомами T _vib може бути близький до кімнатної температури (близько 300 К); наприклад, T _vib ≈ 308 К для газу йоду, I ₂. (Громадське надбання; PD-самоврядування)

Приклад: СО ₂ проти NO ₂

Для порівняння молярних теплоємностей діоксиду азоту і вуглекислого газу при постійному обсязі (при кімнатній температурі) скористаємося законом рівноділення і припустимо коливання, які потрібно заморозити при кімнатній температурі. Прогнозований моляр для лінійної\(CO_2\) (з трьома поступальними і двома обертальними ступенями свободи) є\(5/2R\)\(20.8\, JK^{-1}mo'^{-1})\).

Орієнтовний моляр для\(NO_2\) (зігнута молекула, з трьома поступальними і трьома обертальними ступенями свободи) є\(3R \,(25.0\, JK^{-1}mol^{-1})\). Ці оцінки близькі до експериментальних значень:

• 30.1 JK ^-1 моль ^-1 для\(CO_2\)
• 29,5 JK ^-1 моль ^-1 для\(NO_2\)

Особливо для\(CO_2\), відхилення значне. Це говорить про те, що, хоча не всі вібраційні ступені свободи доступні, їх не можна повністю ігнорувати. Більше відхилення в прогнозуванні молярних теплових потужностей, ймовірно, пов'язано з існуванням нижчої частотно-згинальної вібрації у вуглекислому газу.

Посилання

1. Термодинаміка та статистична механіка, Грейнер В., Нейз, Штокер, Спрінгер, 2001
2. Фізична хімія, 5-е видання, Аткінс П., Фрімен і компанія, 1994.

Дописувачі та атрибуція

• Зейн Стеркевольф (UC Девіс)
• www.chem.iitb.ac.in/~bltemb/pdfs/ch_3.pdf
• Sudarson S Сінха (Тель-Авівський університет)