17.2: Розподіл Больцмана являє собою термічно врівноважений розподіл
- Page ID
- 26726
Розглянемо ансамбль N-частинок. Частинки не обов'язково відрізняються і, можливо, мають взаємну потенційну енергію. Оскільки це велика система, існує безліч різних способів розташувати її частинки і все ж дати однаковий термодинамічний стан. За один раз може відбуватися лише одне розташування. Сума ймовірностей кожного окремого розташування дорівнює загальній кількості окремих домовленостей. Тоді ймовірність виникнення системи становить:
\[p_N=W_N p_i \nonumber \]
де\(p_N\) - ймовірність системи,\(W_N\) - загальна кількість різних можливих розташувань N частинок в системі, і\(p_i\) ймовірність кожного окремого розташування. Принцип невизначеності Гейзенберга стверджує, що неможливо одночасно знати імпульс і положення об'єкта з повною точністю. Відповідно до принципу невизначеності загальна можлива кількість комбінацій може бути визначена як загальна кількість помітних перестановок N частинок.
Самий практичний ансамбль - канонічний ансамбль з\(N\)\(V\), і\(T\) фіксований. Ми можемо уявити собі колекцію коробок з рівними обсягами і кількістю частинок, при цьому вся колекція зберігається в тепловій рівновазі. Виходячи з фактора Больцмана, ми знаємо, що для системи, яка має стани з енергіями\(e_1,e_2,e_3\)..., ймовірність\(p_j\) того, що система буде перебувати в стані\(j\) з енергією\(E_j\), експоненціально пропорційна енергії стану\(j\). Функції розподілу держави відводять дуже важливу роль при розрахунку властивостей системи, наприклад, з її допомогою можна обчислити ймовірність, а також енергію, теплоємність, тиск.
Розподіл Больцмана
Нас в кінцевому рахунку цікавить ймовірність того, що відбудеться даний розподіл. Причина цього полягає в тому, що ми повинні мати цю інформацію, щоб отримати корисні термодинамічні середні показники. Розглянемо ансамбль\(A\) систем. Визначимо\(a_j\) як кількість систем в ансамблі, які знаходяться в квантовому стані\(j\). Наприклад,\(a_1\) представляє кількість систем в квантовому стані 1. Загальна кількість можливих мікростанів становить:
\[W(a_1,a_2,...) = \frac{A!}{a_1!a_2!...} \nonumber \]
Загальна ймовірність того,\(P_j\) що система знаходиться в j-му квантовому стані, отримується шляхом усереднення\(a_j/A\) по всіх дозволених розподілах. Таким чином,\(P_j\) дається:
\[ \begin{align*} P_j &= \dfrac{\langle a_j \rangle}{A} \\[4pt] &= \dfrac{1}{A} \dfrac{ \displaystyle \sum_a W(a) a_j(a)}{\displaystyle \sum_a W(a)} \end{align*} \]
де кутові дужки вказують на середнє значення ансамблю. Використовуючи це визначення, ми можемо обчислити будь-яку середню властивість (тобто будь-яку термодинамічну властивість):
\[ \langle M \rangle = \sum_j M_j P_j \label{avg} \]
Метод найбільш ймовірного розподілу заснований на думці про те, що середнє\(P_j\) перевищення ідентичне найбільш ймовірному розподілу. Фізично це пов'язано з тим, що у нас так багато частинок в типовій системі, що коливання від середнього надзвичайно (незмірно) малі. Еквівалентність середньої ймовірності числа занять і найбільш ймовірного розподілу виражається наступним чином:
\[ P_j = \dfrac{\langle a_j \rangle}{A} = \dfrac{a_j}{A} \nonumber \]
Функція ймовірності підпорядковується наступним обмеженням:
- Обмеження 1: Збереження енергії вимагає:\[ E_{total} = \sum_j a_j e_j \label{con1} \]\(e_j\) де енергія j-го квантового стану.
- Обмеження 2: Збереження маси вимагає:\[ A = \sum_j a_j \label{con2} \] що говорить лише про те, що загальна кількість всіх систем в ансамблі є\(A\).
Як ми дізнаємося в наступних розділах, система буде прагнути до розподілу\(a_j\), що максимізує загальну кількість мікростанів. Це може виражатися у вигляді:
\[\sum_j \left(\dfrac{\partial \ln W }{\partial a_j}\right) = 0 \nonumber \]
Нашими обмеженнями стають:
\[ \sum_j e_j da_j =0 \nonumber \]
\[ \sum_j da_j =0 \nonumber \]
Метод множників Лагранжа (імені Джозефа Луї Лагранжа) є стратегією знаходження локальних максимумів і мінімумів функції, що підлягають обмеженню рівності. Використовуючи метод невизначених множників ЛаГранжа, ми маємо:
\[ \sum_j \left[ \left(\dfrac{\partial \ln W }{\partial a_j}\right)da_j + \alpha da_j - \beta e_j da_j \right] = 0 \nonumber \]
Ми можемо використовувати наближення Стірлінга:
\[\ln x! \approx x\ln x – x \nonumber \]
оцінити:
\[ \left(\dfrac{\partial \ln W }{\partial a_j}\right) \nonumber \]
щоб отримати:
\[ \left(\dfrac{\partial A! }{\partial a_j}\right) - \sum_i \left(\dfrac{\partial \ln a_i }{\partial a_j}\right) = 0 \nonumber \]
як зазначено нижче.
Застосування наближення Стірлінга
Насамперед слід зазначити, що:
\[\ln W = \ln A! - \sum_j \ln a_j! a \approx A \ln A – A - \sum_j a_j \ln a_j - \sum_j a_j \nonumber \]
Оскільки (з рівняння\(\ref{con2}\)):
\[A = \sum_j a_j \nonumber \]
ці два скасовують, щоб дати:
\[\ln W = A \ln A - \sum_j a_j \ln a_j \nonumber \]
Похідною є:
\[ \left(\dfrac{\partial \ln W}{\partial a_j} \right) = \dfrac{\partial A \ln A}{\partial a_j} - \sum_i \dfrac{\partial a_i \ln a_i}{\partial a_j} \nonumber \]
Тому у нас є:
\[\left(\dfrac{\partial A \ln A}{\partial a_j} \right) = \dfrac{\partial A }{\partial a_j} \ln A - \dfrac{\partial A }{\partial a_j} = \ln A -1 \nonumber \]
\[\left(\dfrac{\partial a_i \ln a_i}{\partial a_j} \right) = \dfrac{\partial a_i }{\partial a_j} \ln a_i - \dfrac{\partial a_i }{\partial a_j} = \ln a_j +1 \nonumber \]
Ці останні похідні є результатом того, що:
\[\left( \dfrac{\partial a_i}{\partial a_i} \right) = 1 \nonumber \]
\[\left( \dfrac{\partial a_j}{\partial a_i}\right)=0 \nonumber \]
Просте вираз, яке є результатом цих маніпуляцій:
\[ - \ln \left( \dfrac{a_j}{A} \right) + \alpha - \beta e_j =0 \nonumber \]
Найбільш вірогідним розподілом є:
\[ \dfrac{a_j}{A} = e^a \sum_j e^{-\beta e_j} \label{Eq3} \]
Тепер нам потрібно знайти невизначені множники\(\alpha\) і\(\beta\).
Ліва сторона Рівняння\(\ref{Eq3}\) дорівнює 1. Таким чином, ми маємо:
\[ P_j= \dfrac{a_j}{A} = \dfrac{ e^{-\beta e_j}} {\sum_j e^{-\beta e_j}} \nonumber \]
Це визначає\(a\) і визначає розподіл Больцмана. Ми покажемо, що\(\beta\) з оптимізаційної процедури методу множників Лагранжа є:
\[\beta=\dfrac{1}{kT} \nonumber \]
Ця ідентифікація покаже важливість температури в розподілі Больцмана. Розподіл являє собою термічно врівноважений найбільш ймовірний розподіл по всіх енергетичних рівнях (Рисунок Template:index).
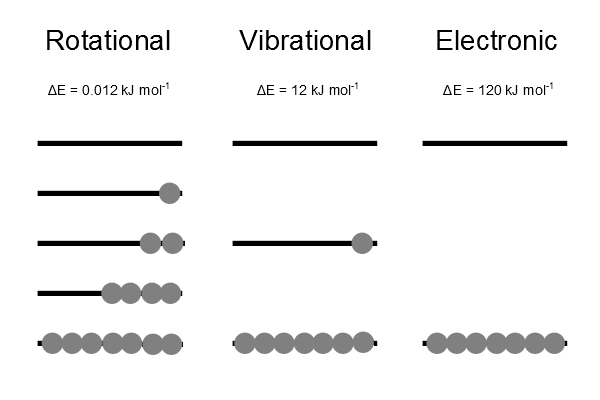
Розподіл Больцмана являє собою термічно врівноважений найбільш ймовірний розподіл по всіх енергетичних рівнях. Завжди є більш висока популяція в стані меншої енергії, ніж в одній з вищих енергій.
Як тільки ми дізнаємось розподіл ймовірностей для енергії, ми можемо обчислити термодинамічні властивості, такі як енергія, ентропія, вільна енергія та теплові потужності, які є середніми величинами (Рівняння\(\ref{avg}\)). Для розрахунку\(P_j\) нам потрібні енергетичні рівні системи (тобто\(\{e_i\}\)). Енергія («рівні») системи може бути побудована з квантових енергетичних рівнів
Завжди потрібно пам'ятати, що незалежно від того, наскільки великий енергетичний інтервал, завжди існує ненульова ймовірність заселення верхнього рівня. Виняток становить лише система, яка знаходиться на абсолютному нулі. Ця ситуація, однак, гіпотетична, оскільки абсолютний нуль може бути наближений, але не досягнутий.
Функція розділу
Сумі над усіма факторами\( e^{-\beta e_j} \) дається назва. Вона називається функцією молекулярного поділу,\(q\):
\[ q = \sum_j e^{-\beta e_j} \nonumber \]
Функція молекулярного поділу\(q\) дає вказівку на середню кількість станів, які термічно доступні молекулі при температурі системи. Функція розділення - це сума над станами (звичайно, з коефіцієнтом Больцмана,\(\beta\) що множить енергію в експоненті) і є числом. Більше значення\(q\), більша кількість станів, які доступні для молекулярної системи для займання (Рисунок Template:index).
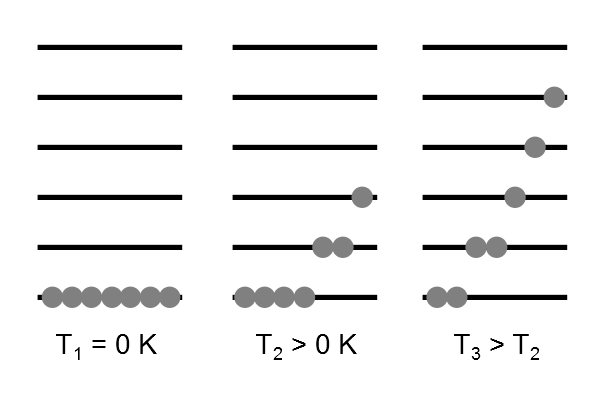
Тут ми розрізняємо функцію розділення ансамблю\(Q\) та окремої молекули\(q\). Оскільки\(Q\) являє собою суму над усіма станами, доступними для системи, вона може записатися як:
\[ Q(N,V,T) = \sum_{i,j,k ...} e^{-\beta ( e_i + e_j +e_k ...)} \nonumber \]
де показники\(i,\,j,\,k\) представляють енергетичні рівні різних частинок.
Незалежно від типу частинки функція молекулярного поділу,\(q\) являє собою енергетичні рівні однієї окремої молекули. Ми можемо переписати вищевказану суму як:
\[Q = q_iq_jq_k… \nonumber \]
або:
\[Q = q^N \nonumber \]
для\(N\) частинок. Зверніть увагу, що\(q_i\) означає суму над станами або енергетичними рівнями, доступними для молекули,\(i\) і\(q_j\) означає те саме для молекули\(j\). Функція молекулярного поділу\(q\) підраховує рівні енергії, доступні\(i\) лише молекулі. \(Q\)підраховує не тільки стани всіх молекул, але і всі можливі комбінації професій цих станів. Однак, якщо частинки не помітні, ми підрахуємо\(N!\) станів занадто багато. \(N!\)Коефіцієнт точно, скільки разів ми можемо поміняти місцями індекси\(Q(N,V,T)\) і отримати однакове значення (знову ж за умови, що частинки не помітні). Дивіться це відео для отримання додаткової інформації.
Посилання
- Хакала, Р.В. Просте обґрунтування форми закону розподілу Больцмана. Журнал хімічної освіти. 44 (11), 657. я: 10,1021/д 044п657
- Григоренко І. Гарсія М.Є. Розрахунок функції розділення за допомогою квантових генетичних алгоритмів. Фізика А: Статистична механіка та її застосування. 313. 463-470. Отримано з http://www.sciencedirect.com/science...78437102009883
Проблеми
- Завершити обґрунтування закону розподілу Больцмана шляхом обчислення константи пропорційності\(a\).
- Система містить два енергетичні рівні\(E_1, E_2\). Використовуючи статистику Больцмана, висловіть середню енергію системи в перерахунку на\(E_1, E_2\).
- Розглянемо, що система містить N енергетичних рівнів. Повторити проблему #2.
- Використовуйте властивість експоненціальної функції, виведіть рівняння (17.9).
- Яке використання функцій розділів?