8.7: Розрахунки Хартрі-Фока дають гарну згоду з експериментальними даними
- Page ID
- 26761
- Зрозумійте, як метод Хартрі розширюється, включивши симетризовані багатоелектронні детерментаційні хвильові функції за допомогою рівнянь Хартрі-Фока.
- Зрозумійте, як обчислити орбітальні енергії з теорії ВЧ.
- Застосовуйте теорію ВЧ з теорією Купмана для оцінки енергій іонізації та спорідненості електронів.
Розглянутий раніше метод Хартрі є корисним як вступ до розв'язання багаточастинкової системи та до понять самоузгодженості та розрахунків самоузгодженого поля, але його значення обмежується історією фізики. Насправді метод Хартрі не просто приблизний, він в корені неправильний, оскільки його хвильова функція не є антисиметричною до перестановки електронів! Розглянутий нижче підхід Хартрі-Фока є кращим підходом, який правильно враховує антисиметричний характер пробних хвильових функцій.
Хоча рівняння Хартрі чисельно простежуються за допомогою методу самоузгодженого поля, не дивно, що таке грубе наближення не може захопити елементи істотної фізики. Принцип виключення Паулі вимагає, щоб хвильова функція багатьох тіл була антисиметричною щодо обміну будь-якими двома електронними координатами, наприклад.
\[\Psi(\mathbf{r}_{1},\mathbf{r}_{2}, \ldots, \mathbf{r}_{N}) = - \Psi(\mathbf{r}_{2},\mathbf{r}_{1}, \ldots, \mathbf{r}_{N}) \label{2.7} \]
які явно не можуть бути задоволені багатоелектронними хвильовими функціями форми, що використовується в наближенні Хартрі, тобто орбітальним наближенням (Рівняння\(\ref{2.3}\)).
\[\Psi(\mathbf{r}_1,\mathbf{r}_2, \ldots, \mathbf{r}_N) \approx \psi_{1}(\mathbf{r}_1)\psi_{2}(\mathbf{r}_2) \ldots \psi_{N}(\mathbf{r}_N) \label{2.3} \]
Ця умова нерозрізненості може бути задоволена формуванням Слейтерівського детермінанта одночастинкових орбіталей.
\[\Psi(\mathbf{r}_{1}, \mathbf{r}_{2}, \ldots, \mathbf{r}_{N})= \dfrac{1}{\sqrt{N}} \left \vert\psi(\mathbf{r}_{1})\psi(\mathbf{r}_{2}) \ldots \psi(\mathbf{r}_{N}) \right\vert \label{2.8} \]
Це відокремлює електрони, що призводять до\(N\) одночастинкових рівнянь Хартрі-Фока:
\[\underbrace{-\dfrac{\hbar^{2}}{2m}\nabla^{2}\psi_{i}(\mathbf{r})}_{\text{kinetic energy}} + \underbrace{V_{nucleus}(\mathbf{r})\psi_{i}(\mathbf{r})}_{\text{electron-nucleus potential}} + \underbrace{V_{electron}(\mathbf{r})\psi_{i}(\mathbf{r})}_{\text{Hartree Term}} - \sum_{j} \int d\mathbf{r}^{\prime} \dfrac{\psi^{\star}_{j}(\mathbf{r}') \psi^{\star}_{i}(\mathbf{r}') \psi_{j}(\mathbf{r}) } {\left \vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} = \epsilon_{i}\psi_{i}(\mathbf{r}). \label{2.9} \]
Як і у випадку з рівняннями Хартрі, перший член - кінетична енергія\(i^{th}\) електрона
\[-\dfrac{\hbar^{2}}{2m}\nabla^{2}\psi_{i}(\mathbf{r}) \nonumber \]
а другий термін - електронно-ядерний потенціал між\(i^{th}\) електроном і ядром
\[V_{nucleus}(\mathbf{r})\psi_{i}(\mathbf{r}) \nonumber \]
Третій термін (іноді його називають терміном «Хартрі») - це електростатичний потенціал між\(i^{th}\) електроном і середнім розподілом заряду інших електронів N-1.
\[V_{electron}(\mathbf{r})\psi_{i}(\mathbf{r}) = J_{j,k} = \int |\phi_j(r)|^2 |\phi_k(r’)|^2 \dfrac{e^2}{r-r'} dr dr’ \label{8.3.9} \]
Ці три члени ідентичні рівнянню Хартрі з добутком хвильової функції ansatz (тобто орбітального наближення). Четвертого члена рівняння\(\ref{2.9}\) немає в рівняннях Хартрі:
\[\sum_{j} \int d\mathbf{r}^{\prime} \dfrac{\psi^{\star}_{j}(\mathbf{r}') \psi^{\star}_{i}(\mathbf{r}') \psi_{j}(\mathbf{r}) } {\left \vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} \nonumber \]
і є терміном обміну. Цей термін нагадує прямий кулонівський термін, але для обмінних індексів. Це прояв принципу виключення Паулі, і діє так, щоб відокремити електрони одного і того ж спіна. Цей термін «обміну» діє тільки на електрони з однаковим спіном і походить від детермінантної форми Слейтера хвильової функції. Фізично ефект обміну полягає в тому, щоб односпінові електрони уникали один одного. Термін обміну значно додає складності цих рівнянь.
Рівняння Хартрі-Фока в рівнянні\(\ref{2.9}\) можна переробити як ряд рівнянь Шредінгера:
\[ \hat {F} | \varphi _i \rangle = \epsilon _i| \varphi _i \rangle \label {8.7.2} \]
де\(\hat {F}\) називається оператором Фока і\( \{| \varphi_i \rangle \}\) є орбіталями Хатрі-Фока з відповідними енергіями\(\epsilon_i\).
Оператор Фока є одноелектронним оператором і розв'язування рівняння Хартрі-Фока дає енергію і орбіталь Хартрі-Фока для одного електрона. Для системи з 2N електронами змінна i буде коливатися від 1 до N; тобто для кожної орбіти буде одне рівняння. Причина цього полягає в тому, що в Рівнянні використовуються лише просторові хвильові функції\(\ref{8.7.2}\). Оскільки просторова частина орбіти може бути використана для опису двох електронів, кожна з енергій та хвильових функцій, знайдених рішенням Рівняння,\(\ref{8.7.2}\) буде використана для опису двох електронів.
Природа оператора Фока показує, як метод Хартрі-Фока (HF) або самоузгодженого поля (SCF) враховує електронно-електронну взаємодію в атомах і молекулах, зберігаючи ідею незалежних атомних орбіталів. Хвильова функція, записана як детермінант Слейтера спин-орбіталів, необхідна для отримання форми оператора Фока, який є
\[\hat {F} = \hat {H} ^0 + \sum _{j=1}^N ( 2 \hat {J} _j - \hat {K} _j ) = -\dfrac {\hbar ^2}{2m} \nabla ^2 - \dfrac {Ze^2}{4 \pi \epsilon _0 r} + \sum _{j=1}^N (2\hat {J}_j - \hat {K} _j ) \label {8.7.3} \]
Як показує розширена версія на крайньому правому куті, перший член цього рівняння - це знайомий водень подібний оператор\(\hat {H}^0\), який враховує кінетичну енергію електрона та потенційну енергію цього електрона, що взаємодіє з ядром. Наступний термін припадає на потенційну енергію одного електрона в середньому полі, створеному всіма іншими електронами в системі. \(\hat {K}\)Оператори\(\hat {J}\) та є результатом умов відштовхування електронів у повному гамільтоні для багатоелектронної системи. Ці оператори включають одноелектронні орбіталі, а також енергію взаємодії електрон-електронів.
Оператор Фока (Equation\(\ref{8.7.3}\)) залежить від усіх зайнятих орбіталей (через операторів обміну та Кулона). Тому конкретну орбіту можна визначити тільки в тому випадку, якщо всі інші відомі. Необхідно використовувати ітераційні методи для вирішення рівнянь ВЧ, таких як метод самоузгодженого поля, розглянутий раніше для наближення Хартрі.
Взаємодія обміну - це квантовий механічний ефект, який відбувається лише між однаковими частинками. Незважаючи на те, що іноді називають обмінною силою за аналогією з класичною силою, вона не є справжньою силою, оскільки їй не вистачає носія сили. Ефект обумовлений хвильовою функцією нерозрізнених частинок, що піддаються обмінній симетрії, тобто або залишаються незмінними (симетричними), або змінюють свій знак (антисиметричний) при обміні двома частинками. Як бозони, так і ферміони можуть відчувати обмінну взаємодію. Для ферміонів його іноді називають відштовхуванням Паулі і пов'язане з принципом виключення Паулі. Для бозонів обмінна взаємодія набуває форми ефективного тяжіння, що змушує ідентичні частинки знаходитися ближче один до одного, як при конденсації Бозе—Ейнштейна.
Наприклад, електрон 1 в гелії (з\(Z=2\)), потім
\[\hat {H}^0 (1) = - \dfrac {\hbar ^2}{2m} \nabla ^2_1 - \dfrac {2e^2}{4 \pi \epsilon _0 r_1} \label {8.7.4} \]
Оператор Фока складається з точки зору координат одного електрона, перспективу якого ми приймаємо (який ми будемо називати електроном 1 протягом усього наступного обговорення), а середнє поле, створене всіма іншими електронами в системі, будується з точки зору координат родового» інший електрон» (який ми будемо називати електроном 2), який вважається займати кожну орбіталь по черзі під час підсумовування над N просторовими орбіталями.
Як і у випадку з рівняннями Хартрі, рішення рівнянь Хартрі-Фока математично еквівалентно припущенню, що кожен електрон взаємодіє лише з середньою хмарою заряду інших електронів. Ось так обробляється електронно-електронне відштовхування. Саме тому цей підхід також називають підходом до самопослідовного поля (SCF).
Найкращі можливі одноелектронні хвильові функції, за визначенням, дадуть найменшу можливу сумарну енергію для багатоелектронної системи, що використовується з повним мультиелектронним гамільтоном для обчислення очікуваного значення для загальної енергії системи. Ці хвильові функції називаються хвильовими функціями Хартрі-Фока, а розрахункова загальна енергія - енергія Хартрі-Фока системи.
Хартрі-Фок Енергія
Рівняння Хартрі-Фока мають на\(h_e \phi_i = \epsilon_i \phi_i\) увазі, що орбітальні енергії\(\epsilon_i\) можна записати як:
\[ \begin{align*} \epsilon_i &= \langle \phi_i | h_e | \phi_i \rangle \\[4pt] &= \langle \phi_i | T + V | \phi_i \rangle + \sum_{j({\rm occupied})} \langle \phi_i | J_j - K_j | \phi_i \rangle \label{8.7.6} \\[4pt] &= \langle \phi_i | T + V | \phi_i \rangle + \sum_{j({\rm occupied})} [ J_{i,j} - K_{i,j} ],\label{8.7.7} \end{align*} \]
де\(T + V\) представляє кінетичну (\(T\)) і ядерну енергію тяжіння (\(V\)) відповідно. Таким чином,\(\epsilon_i\) середнє значення кінетичної енергії плюс кулонівського тяжіння до ядер для електрона\(\phi_i\) плюс сума над усіма спін-орбіталями, зайнятими в\(\psi\) Кулонівському мінус Обмінні взаємодії цих електронів з електроном в\(\phi_i\).
Якщо\(\phi_i\) це зайнята спин-орбіталь,\(j = i\) термін\([ J_{i,i} - K_{i,i}]\) зникає у вищевказаній сумі, а інші члени в сумі представляють кулонівську мінус обмінну взаємодію\(\phi_i\) з усіма\(N-1\) іншими займаними спин-орбіталями. Якщо\(\phi_i\) це віртуальний спін-орбітальний, це скасування не відбувається, оскільки сума понад\(j\) не включає\(j = i\). Таким чином, отримується Кулон мінус обмінної взаємодії\(\phi_i\) з усіма\(N\) займаними спин-орбіталями в\(\psi\). Отже, енергії зайнятих орбіталів відносяться до взаємодій, відповідних загальній кількості\(N\) електронів, тоді як енергії віртуальних орбіталів відносяться до системи з\(N+1\) електронами. Цю різницю дуже важливо розуміти і мати на увазі.
Щоб дати уявлення про те, наскільки добре теорія ВЧ може передбачити енергії основного стану декількох атомів, розглянемо таблицю Template:index нижче:
| Атом | Хартрі-Фок Енергія | Експеримент |
|---|---|---|
| \(He\) | \(-5.72\) | \(-5.80\) |
| \(Li\) | \(-14.86\) | \(-14.96\) |
| \(Ne\) | \(-257.10\) | \(-257.88\) |
| \(Ar\) | \(-1053.64\) | \(-1055.20\) |
Теорема Купмана
Теорема Купмана стверджує, що перша енергія іонізації дорівнює негативній орбітальної енергії найвищої зайнятої молекулярної орбіталі. Отже, енергія іонізації, необхідна для створення катіона та відокремленого електрона, представлена видаленням електрона з орбіти без зміни хвильових функцій інших електронів. Це називається «заморожене орбітальне наближення». Розглянемо наступну модель відшарування або приєднання електрона в\(N\) електронну систему.
- У цій моделі як материнська молекула, так і види, що генеруються додаванням або видаленням електрона, обробляються на однодетермінантному рівні.
- Орбіталі Хартрі-Фока материнської молекули використовуються для опису обох видів. Кажуть, що така модель нехтує орбітальної релаксацією (тобто повторною оптимізацією спин-орбіталей, щоб дозволити їм стати відповідними дочірнім видам).
В рамках цієї моделі різниця енергії між дочкою і батьком може бути записана наступним чином (\(\phi_k\)являє собою конкретний спін-орбіталь, який додається або видаляється:
- для відшарування електронів (енергії вертикальної іонізації)\[ \color{red} E_{N-1} - E_N = - \epsilon_k \label{8.7.8} \]
- і для приєднання електронів (спорідненість електронів)\[ \color{red} E_N - E_{N+1} = - \epsilon_k .\label{8.7.9} \]
Виведемо цей результат для випадку, коли електрон додається до\(N+1^{st}\) спін-орбіталі. Енергія\(N\) електронного детермінанта зі спін-орбіталями\(\phi_1\) через\(f_N\) окуповані становить
\[E_N = \sum_{i=1}^N \langle \phi_i | T + V | \phi_i \rangle + \sum_{i=1}^{N} [ J_{i,j} - K_{i,j} ] \nonumber \]
який також може бути записаний як
\[E_N = \sum_{i=1}^N \langle \phi_i | T + V | \phi_i \rangle + \frac{1}{2} \sum_{i,j=1}^{N} [ J_{i,j} - K_{i,j} ].\nonumber \]
Аналогічно, енергія\(N+1\) -електронного детермінантної хвильової функції є
\[E_{N+1} = \sum_{i=1}^{N+1} \langle \phi_i | T + V | \phi_i \rangle + \frac{1}{2} \sum_{i,j=1}^{N+1} [ J_{i,j} - K_{i,j} ]. \nonumber \]
Різниця між цими двома енергіями дається
\[ \begin{align*} E_{N} – E_{N+1} = &- \langle \phi_{N+1} | T + V | \phi_{N+1} \rangle - \frac{1}{2} \sum_{i=1}^{N+1} [ J_{i,N+1} - K_{i,N+1} ] \\[4pt] &- \frac{1}{2} \sum_{j=1}^{N+1} [ J_{N+1,j} - K_{N+1,j} ] \\[4pt] &= - \langle \phi_{N+1} | T + V | \phi_{N+1} \rangle - \sum_{i=1}^{N+1} [ J_{i,N+1} - K_{i,N+1} ] \\[4pt] &= - \epsilon_{N+1}. \end{align*} \nonumber \]
Тобто різниця енергій дорівнює мінус виразу для енергії\(N+1^{st}\) спін-орбіталі, яке було дано раніше.
Рівняння Хартрі-Фока точно стосуються обміну; однак рівняння нехтують більш детальними кореляціями через взаємодію багатьох тіл. Ефекти електронних кореляцій не є незначними; дійсно нездатність теорії Хартрі-Фока успішно включити кореляцію призводить до однієї з найвідоміших невдач.
У Копенгагенській інтерпретації квадратний модуль хвильової функції дає ймовірність знаходження частинки в заданому місці. Багатотільна хвильова функція дає функцію розподілу N-частинок,\(|Φ(r_1, ..., r_N )|^2\) тобто щільність ймовірності того, що частинка 1 знаходиться в\(r_1\),..., а частинка\(N\) знаходиться в\(r_N\). Однак при спробі відпрацювати взаємодію між електронами ми хочемо знати ймовірність знаходження електрона при\(r\), враховуючи положення всіх інших електронів\(\{r_i\}\). Це означає, що електрон поводиться квантово механічно, коли ми оцінюємо його хвильову функцію, але як класична точкова частинка, коли він сприяє потенціалу, який бачать інші електрони.
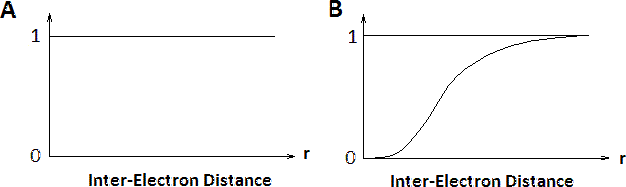
Внесок електронно-електронних взаємодій у n-електронних системах у методах Хартрі та Хартрі-Фока показано на рисунку Template:index. Умовні електронні імовірнісні розподіли\(n(r)\)\(N-1\) електронів навколо електрона з заданим спіном, розташованим на\(r=0\). У межах наближення Хартрі всі електрони розглядаються як незалежні,\(n(r)\) тому безструктурні. Однак в межах наближення Хартрі-Фока хвильова функція\(N\) -електронна відображає принцип виключення Паулі, і поблизу електрона в\(r=0\) обмінній дірці можна побачити, де зменшується щільність спінів, рівна щільності центрального електрона. Електрони з протилежними спинами не впливають (не показані).
Резюме
Так, в межах ВЧ, заморожено-орбітальної моделі потенціали іонізації (ІП) і електронні спорідненості (ЕА) задаються як негативні займаної і віртуальної спін-орбітальної енергій відповідно. Це твердження називають теоремою Купмана; воно широко використовується в квантово-хімічних розрахунках як засіб оцінки потенціалів іонізації (рівняння\(\ref{8.7.8}\)) та електронних спорідненностей (рівняння\(\ref{8.7.9}\)) і часто дає результати, які є якісно правильними (тобто ± 0,5 еВ). Загалом теорія Хартрі-Фока дає велике рішення першого порядку (99%) для опису багатоелектронних систем, але останній 1% все ще занадто великий для кількісного опису багатьох аспектів хімії, і необхідні більш складні підходи. Вони обговорюються в інших місцях.